Kysy velholta #253
En ymmärrä, miten Texas Hold 'Emin power-taulukoissasi A-7 on alemmalla sijalla kuin KJ samasta maasta, mutta laskimessasi A7:llä on suurempi voittotodennäköisyys.
Hyvä kysymys. Muiden lukijoiden tiedoksi tässä ovat todennäköisyydet satunnaista kättä vastaan kummallakin näistä kahdesta aloituskädestä kahden pelaajan pelissä:
KJ samassa maassa vs. A-7 eri maasta
| Käsi | Voittaa | Menettää | Piirrä | Odotusarvo |
K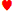 J J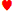 | 0,6148 | 0,3634 | 0,0218 | 0,2513 |
A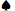 7 7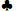 | 0,5717 | 0,3949 | 0,0334 | 0,1768 |
Kahden pelaajan Texas Hold 'em -laskurini mukaan näiden kahden käden todennäköisyydet ovat kuitenkin vastakkain:
A7 voittaa = 53,52 %
KJ voittaa = 46,10 %
Tasapeli = 0,39 %
Joten KJ samaa maata oleva on taulukossani korkeammalla sijalla, mutta huonommalla sijalla kuin A7 eri maata oleva. Miksi?
Vastausta on vaikea selittää. Kun kaksi kättä pelaa toisiaan vastaan, on otettava huomioon, miten ne vaikuttavat toisiinsa. Esimerkiksi aloituskäsien vahvuustaulukossa AK-käsi on vain hieman parempi kuin AQ-käsi, odotusarvoilla 0,3064 ja 0,2886. Jos ne kuitenkin laitetaan vastakkain, AK murskaa AQ:n seuraavasti:
AK voitot = 71,72 %
AQ-voitot = 23,69 %
Tasapeli = 4,58 %
Eri maata olevien A7- ja KJ-käsissä ässä on suurempi kuin kuningas ja jätkä. KJ-pelaajan suurimmat voittomahdollisuudet ovat, jos hän saa K:n tai J:n pariksi eikä ässää tule esiin. Osoitan, että tämän todennäköisyys on vain 37,73 %. Loput 46,10 %:n KJ-voiton todennäköisyydestä tulee korkeammista käsistä.
Vaikka A7 on vahva KJ:tä vastaan, satunnaiset kädet dominoivat sitä useammin kuin KJ:tä.
Ehkä tämä on huono vertaus, mutta se on vähän kuin kivi-paperi-sakset- peli. Taitavien pelaajien keskuudessa jokaisella heitolla pitäisi olla suunnilleen sama voima. Jos kuitenkin toinen pelaaja heittää paperia ja toinen saksia, voimaluokituksilla ei ole merkitystä, ja sakset voittavat.
Las Vegasin Bighornissa ja Longhornissa blackjackissa sallitaan kolmen kortin tuplaaminen. Pitäisikö minun tehdä jotain strategiamuutoksia tämän säännön nojalla?
Wizard of Vegas -sivustoni lukija sanoo, että seuraavat muutokset tulisi tehdä verrattuna tavalliseen usean pakan strategiaan , jossa jakaja saa pehmeän 17:n:
- Lyönti pehmeästi 13 vs. 5 tai 6
- Lyö 2 kortin pehmeä 15 vs. 4
- Osuma 3, 3 vs. 2
Pehmeiden käsien saamisen syy on se, että saatat saada paremman pehmeän tuplan osuman jälkeen. Kolmosten saamisen arvo on suurempi tämän säännön mukaisesti, koska ässän saaminen olisi hyvä kolmen kortin tuplaus.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Jos kolikkoa heitetään 100 kertaa, mikä on todennäköisyys saada vähintään kerran peräkkäin vähintään seitsemän kruunan putki?
Jos vastaukselle on olemassa helppo, ei-rekursiivinen lauseke, en ole siitä tietoinen. On kuitenkin olemassa helppo rekursiivinen vastaus.
f(n)= pr(ensimmäisen käännöksen hännät)×f(n-1) +
pr(krunkki ensimmäisessä käännöksessä, klaava toisessa käännöksessä)×f(n-2) +
pr(kruuna kahdessa ensimmäisessä voltissa, klaava kolmannessa voltissa)×f(n-3) +
pr(kruna kolmella ensimmäisellä heitolla, klaava kolmannella heitolla)×f(n-4) +
pr(kruna neljässä ensimmäisessä heitossa, klaava neljännessä heitossa)×f(n-5) +
pr(kruuna viidessä ensimmäisessä heitossa, klaava viidennessä heitossa)×f(n-6) +
pr(kuuden ensimmäisen heiton kruuna, kuudennen heiton klaava)×f(n-7) +
pr(pää seitsemän ensimmäisen heiton aikana) =
(1/2) × f(n-1) +
(1/2) 2 × f(n-2) +
(1/2) 3 × f(n-3) +
(1/2) 4 × f(n-4) +
(1/2) 5 × f(n-5) +
(1/2) 6 × f(n-6) +
(1/2) 7 × f(n-7) +
(1/2) 7
Jossa:
f(n) = onnistumistodennäköisyys n voltin sisällä.
pr(x) = x:n tapahtuman todennäköisyys.
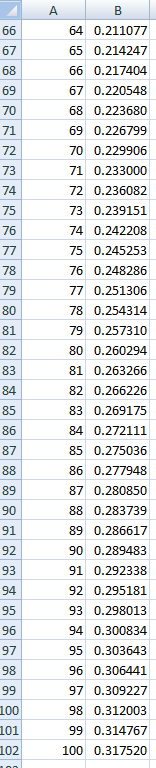
Taulukkolaskentaohjelmat sopivat täydellisesti tällaisiin ongelmiin. Alla olevissa laskentataulukon kuvakaappauksissa olen asettanut soluille B2–B8 todennäköisyydeksi 0, koska kuudessa tai vähemmässä heitossa ei voi olla seitsemää kruunaa peräkkäin. Solulle B9 olen asettanut kaavan:
=(1/2)*B8+(1/2)^2*B7+(1/2)^3*B6+(1/2)^4*B5+(1/2)^5*B4+(1/2)^6*B3+(1/2)^7*B2+(1/2)^7
Sitten kopioin ja liitin sen soluista B10 soluun B102, mikä vastaa 100 volttia. Todennäköisyys on 0,317520. Satunnainen simulaatio vahvistaa sen.
 |  |
Tämän alkuperäisen julkaisun jälkeen Rick Percy jakoi kanssani matriisialgebraratkaisunsa. Tässä se omin sanoin. Oletan, että lukija tuntee jo matriisialbegran perusteet.
Ensinnäkin, räpylä voi olla kahdeksassa mahdollisessa tilassa millä tahansa hetkellä:
p 1 = Onnistumisen todennäköisyys, olettaen, että tarvitset 7 päätä lisää nykyisestä pisteestä.
p 2 = Onnistumisen todennäköisyys, olettaen, että nykyisestä pisteestä tarvitaan vielä 6 päätä.
p 3 = Onnistumisen todennäköisyys, olettaen, että tarvitset 5 kruunaa lisää nykyisestä pisteestä.
p 4 = Onnistumisen todennäköisyys, olettaen, että nykyisestä pisteestä tarvitaan vielä 4 kruunaa.
p 5 = Onnistumisen todennäköisyys, olettaen, että nykyisestä pisteestä tarvitaan vielä 3 kruunaa.
p 6 = Onnistumisen todennäköisyys, olettaen, että nykyisestä pisteestä tarvitaan kaksi lisäpäätä.
p 7 = Onnistumisen todennäköisyys, olettaen, että tarvitset yhden kruunan lisää nykyisestä pisteestä.
p 8 = Onnistumisen todennäköisyys, olettaen, että et tarvitse enempää päitä = 1.
Määritellään maksriksi S n todennäköisyytenä olla kussakin tilassa n :nnen käännöksen jälkeen. S 0 edustaa todennäköisyyksiä ennen ensimmäistä käännettä, jolloin on 100 %:n mahdollisuus olla tilassa 0. Joten S 0 =
| 1 0 0 0 0 0 0 0 0 |
Olkoon T kahden peräkkäisen käännöksen muunnosmatriisi eli S n > S n+1 , missä S n+1 = T × S n
- Jos olet tilassa 1, niin yhden voltin jälkeen sinulla on 0,5 mahdollisuus olla tilassa 2 (kruuna) ja 0,5 mahdollisuus pysyä tilassa 1 (klaava).
- Jos olet tilassa 2, niin yhden voltin jälkeen sinulla on 0,5 mahdollisuus olla tilassa 3 (kruuna) ja 0,5 mahdollisuus palata tilaan 1 (klaava).
- Jos olet tilassa 3, niin yhden voltin jälkeen sinulla on 0,5 mahdollisuus olla tilassa 4 (ja saada kruuna) ja 0,5 mahdollisuus palata tilaan 1 (ja saada klaava).
- Jos olet tilassa 4, niin yhden voltin jälkeen sinulla on 0,5 mahdollisuus olla tilassa 5 (kruuna) ja 0,5 mahdollisuus palata tilaan 1 (klaava).
- Jos olet tilassa 5, niin yhden voltin jälkeen sinulla on 0,5 mahdollisuus olla tilassa 6 (kruuna) ja 0,5 mahdollisuus palata tilaan 1 (klaava).
- Jos olet tilassa 6, niin yhden voltin jälkeen sinulla on 0,5 mahdollisuus olla tilassa 7 (kruuna) ja 0,5 mahdollisuus palata tilaan 1 (klaava).
- Jos olet tilassa 7, niin yhden voltin jälkeen sinulla on 0,5 mahdollisuus olla tilassa 8 (ja saada kruuna) ja 0,5 mahdollisuus palata tilaan 1 (ja saada klaava).
- Jos olet tilassa 8, olet saavuttanut onnistumisen ja pysyt tilassa 8 todennäköisyydellä 1,0.
Laittamalla kaikki tämä siirtymämatriisin T muotoon =
| 0,5 0,5 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,0 |
| 0,5 0,0 0,5 0,0 0,0 0,0 0,0 0,0 0,0 0,0 |
| 0,5 0,0 0,0 0,5 0,0 0,0 0,0 0,0 0,0 0,0 |
| 0,5 0,0 0,0 0,0 0,5 0,0 0,0 0,0 0,0 0,0 |
| 0,5 0,0 0,0 0,0 0,0 0,5 0,0 0,0 0,0 |
| 0,5 0,0 0,0 0,0 0,0 0,0 0,0 0,5 0,0 0,0 |
| 0,5 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,5 0,0 |
| 0,5 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,5 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 |
Päästäkseen kunkin tilan todennäköisyyteen yhden käännöksen jälkeen...
(1) S1 = S0 × T
Entä kahden käännöksen jälkeen?
(2) S2 = S1 × T
Sijoitetaan yhtälö (1) yhtälöön (2)...
(3) S2 = S0 × T × T = S0 × T2
Entä kolmen käännöksen jälkeen?
(4) S3 = S2 × T
Sijoittamalla yhtälö (3) yhtälöön (4)...
(5) S3 = S0 × T2 × T = S0 × T3
Voimme jatkaa tätä aina osavaltioon asti sadannen voltin jälkeen...
S 100 = S 0 × T 100
Mikä sitten on T 100 ? Ennen tietokoneita tällaisten asioiden selvittäminen on täytynyt olla valtavan hankalaa. Excelin MMULT-funktiolla ja paljon kopioimalla ja liittämällä saadaan kuitenkin T 100 =
| 0,342616 0,171999 0,086347 0,043347 0,021761 0,010924 0,005484 0,317520 |
| 0,339863 0,170617 0,085653 0,042999 0,021586 0,010837 0,005440 0,323005 |
| 0,334379 0,167864 0,084271 0,042305 0,021238 0,010662 0,005352 0,333929 |
| 0,323454 0,162380 0,081517 0,040923 0,020544 0,010313 0,005178 0,355690 |
| 0,301693 0,151455 0,076033 0,038170 0,019162 0,009620 0,004829 0,399038 |
| 0,258346 0,129694 0,065109 0.032686 0,016409 0,008237 0,004135 0,485384 |
| 0,171999 0,086347 0,043347 0,021761 0,010924 0,005484 0,002753 0,657384 |
| 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000 |
Oikeassa yläkulmassa oleva termi näyttää todennäköisyyden olla tilassa 8 100 voltin jälkeen, joka on 0,317520.
Äskettäin Toscanan kasino järjesti kampanjan, jossa 30 blackjackin voittamisesta 30 päivän aikana sai 100 dollarin bonuksen. Aluksi minimipanos oli 5 dollaria kortin leimaamiseksi. Myöhemmin kuitenkin kuulin, että leiman minimipanos nostettiin 15 dollariin. Kirjoitin asiasta valituskirjeen kasinon johtajalle, jossa totesin muun muassa seuraavaa:
Halusin vain ilmaista pettymykseni tähän muutokseen, jos se on totta. Minulla ei koskaan ollut mahdollisuutta hyödyntää kampanjaa, ja epäilen, että pystyn siihen nytkään. 30 blackjackin saamiseen tarvittava aika (minulle kerrottiin noin 8 tuntia jatkuvaa pelaamista) tuntuu kohtuuttomalta, 15 dollaria/käsi, kun kampanjassa tarjotaan edelleen vain 100 dollaria.
Tässä on saamani vastaus:
Vastauksena sähköpostiisi blackjackin katkoskampanjasta, en ole varma, mistä sait tietosi siitä, kuinka kauan katkoskortin täyttäminen kestää. Olemme nähneet pelaajien täyttävän kortin alle neljässä tunnissa. Sinulla on myös 30 päivää aikaa täyttää kortti. Toivon, että ymmärrät, että tämä ei ole tehtävä, johon ei olisi mahdotonta päästä niin pitkässä ajassa. KIITOS kirjeestäsi. On hyvä kuulla palautetta asiakkailtamme. Toivottavasti voit kokeilla sitä ja voittaa rahaa!
Mikä on todennäköisyys saada 30 blackjackia neljässä tunnissa?
Todennäköisyys saada kortti täyteen neljässä tunnissa, olettaen 280 kättä, on 1/30 000, jos pelataan yksi käsi kerrallaan. Epäilen, että jokainen pelaaja, joka saavutti tavoitteen neljässä tunnissa, pelasi vähintään kaksi kättä kerrallaan.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.


