Kysy velholta #259
Jotkut hollantilaiset kasinot sallivat kolminkertaisen vankeusrangaistuksen ruletissa. Mikä on talon etu tasarahapanoksissa tämän säännön nojalla? Olen kiinnostuneempi ratkaisusta kuin vastauksesta.
Muiden lukijoiden tiedoksi, monissa eurooppalaisissa kasinoissa ruletissa panostetaan tasarahalla, jos kuula pysähtyy nollaan. Jos seuraava heitto toisi voiton, panos palautetaan ilman voittoja. Jos kuula pysähtyy vastakkaiseen suuntaan, panos häviää.
Mitä tapahtuu kertavankeuspanoksille, jos pallo pysähtyy nollaan? Jos kasino sallii vain kertavankeusrangaistuksen, se häviää. Jotkut kasinot kuitenkin sallivat kaksinkertaisen vankeusrangaistuksen, ja näin tapahtuukin. Jos kaksinkertaisella vankeusrangaistuksella tehty panos voittaa, se palaa kertavankeusrangaistukseen. Jos kasino sallii vain enintään kaksinkertaisen vankeusrangaistuksen, kaksinkertaisella vankeusrangaistuksella tehty panos häviää toisella nollalla. Samalla logiikalla, jos kasino sallii kolminkertaisen vankeusrangaistuksen, kaksinkertaisella vankeusrangaistuksella tehty panos muuttuu kolminkertaiseksi vankeusrangaistukseksi toisella nollalla.
Talon etu kolmoisvankeusrangaistuksessa on 1,370120 %. Ennen kuin selitän, miten päädyin tähän, tarkastellaan ensin yksi- ja kaksinkertaista vankeusrangaistusta. Oletetaan, että ensimmäinen panos on punaiselle.
Olkoon Z = nollan todennäköisyys = 1/37.
Olkoon R = punaisen luvun todennäköisyys = 18/37.
Yksittäinen vankeusrangaistus
pr(työntö) = ZR = 0,0131482834.
pr(voitto) = R = 0,4864864865.
pr(tappio) = 1-pr(push)-pr(voitto) = 0,5003652301.
Odotusarvo = pr(voitto) - pr(tappio) = -0,0138787436.
Kaksinkertainen vankeusrangaistus
Pelaaja työntää, jos ensimmäinen pyöräytys on nolla, niin pelaaja voi toistaa ZR:n nollasta äärettömän monta kertaa ja saada sitten punaisen. Toisin sanoen, työntämisen tavat ovat:
ZR, Z(ZR)R, Z(ZR)(ZR)R, Z(ZR)(ZR)(ZR)R, ...
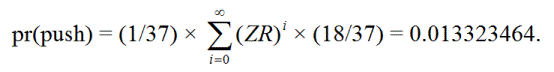
pr(työntö) = 0,013323464
pr(voitto) = 18/37 = 0,4864864865.
pr(tappio) = 1-pr(push)-pr(voitto) = 0,5001900494.
Odotusarvo = pr(voitto) - pr(tappio) = -0,0137035629.
Kolminkertainen vankeusrangaistus
Etsitään ensin todennäköisyys p 1 sille, että yksinkertaisesti vangittu veto muuttuu kolminkertaisesti vangituksi kahdella nollalla lisää ja lopulta nousee takaisin yksinkertaisesti vangituksi. Tämä voi tapahtua seuraavasti:
ZZRR, ZZ(RZ)RR, ZZ(RZ)(RZ)RR, ZZ(RZ)(RZ)(RZ)RR, ...
Toisin sanoen panos voi vaihdella kolminkertaisen ja kaksinkertaisen vangitsemisen välillä jopa äärettömän monta kertaa.
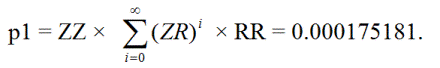
Toiseksi, olkoon p 2 = todennäköisyys sille, että yksittäinen vankeusrangaistus saavuttaa ensimmäisen tai toisen vankeusrangaistustason ja palaa sitten yksittäiseen vankeusrangaistukseen.
Olkoon p² = ZR + p¹ = 0,013323464.
Pelaaja voi palata ensimmäiselle tasolle nollasta äärettömän monta kertaa. Joten puskemisen todennäköisyys on:
ZR + Zp 2R + Zp 2p 2R + Zp 2p 2R + ... =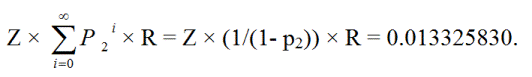
Z × (1/(1 - p2 )) × R = 0,013325830.
pr(työntö) = 0,013325830.
pr(voitto) = 18/37 = 0,4864864865.
pr(tappio) = 1-pr(push)-pr(voitto) = 0,5001876839.
Odotusarvo = pr(voitto) - pr(tappio) = -0,0137011974.
Ääretön vankeus
Ei niin, että kysyit, Maff, mutta kuulin, että Espanjassa sallitaan ääretön vangitseminen. Olkoon p = työntötodennäköisyys. Tämä on myös todennäköisyys aloittaa vangitsemisen tasolta x, pudota syvemmälle tasoille ja lopulta kiivetä takaisin tasolle x.
p = ZR + ZpR + ZppR + ZpppR + ...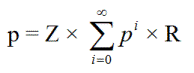
p2 - p + ZR = 0
Toisen asteen kaavan mukaan p = (1-(1-4*RZ) ^1/ 2)/2 = 0,0133258620.
pr(työntö) = 0,0133258620.
pr(voitto) = 18/37 = 0,4864864865.
pr(tappio) = 1-pr(push)-pr(voitto) = 0,5001876515.
Odotusarvo = pr(voitto) - pr(tappio) = -0,0137011650.
Nollat jättivät vankeusrangaistuksen huomiotta
Lopuksi, joissakin kasinoissa nollat yksinkertaisesti jätetään huomiotta ensimmäisen nollan jälkeen, mikä vangitsee panoksen. Näissä tasapelin todennäköisyys on yksinkertaisesti (1/37) × (1/2) = 0,0135135135.
Seuraavassa taulukossa on yhteenveto kaikista neljästä sääntötyypistä.
Vankeusrangaistuksen kertoimet
| Vankeusrangaistus | Voittaa | Työnnä | Menetys | Odotettu Arvo |
| Yksittäinen | 0.48648649 | 0.01314828 | 0.50036523 | -0,01387874 |
| Kaksinkertainen | 0.48648649 | 0.01332346 | 0.50019005 | -0,01370356 |
| Kolminkertaistaa | 0.48648649 | 0,01332583 | 0.50018768 | -0,01370120 |
| Ääretön | 0.48648649 | 0,01332586 | 0.50018765 | -0,01370117 |
| Nollat jätetään huomiotta | 0.48648649 | 0.01351351 | 0,50000000 | -0,01351351 |
Haluan kiittää ChesterDogia ja weaselmania heidän matemaattisesta avustaan. Haluan myös kiittää ja suositella professori G. Articoa ja polarprof.it-sivustoa yllä olevan summakaavan HTML-koodista.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Oletetaan, että seuraava pitää paikkansa yhdestä videopokeriautomaatista.
- 6-5 Bonus Poker progressiivinen.
- 2 % metrin nousu kuningasvärisuorassa.
- 5 kolikon peli.
Oletetaan nyt minusta seuraavaa.
- Minimipalautusprosentti peliin on 100,5 %.
- Pystyn pelaamaan progressiivista pöytäpeliä, kunnes se iskee.
- Tiedän täydellisen 6-5 Bonus Poker -strategian 4000 kolikon kuninkaalliselle pokerille.
Mikä on pienin jackpot, jolla minun pitäisi pelata?
7 281,8 kolikkoa. On mielenkiintoista huomata, että jos pelaisit vain kerran täsmälleen tuolla mittarilla, palautus olisi vain 98,5 %. Syy siihen, miksi sinun pitäisi pelata siinä vaiheessa, on se, että oletetaan, että pystyt pelaamaan, kunnes voitat jättipotin. Se on kuin sinulla olisi 2 %:n käteispalautuskolikkopeli. 98,5 % + 2 % = 100,5 %.
Voisin lisätä, että jos aloitat 4000 kolikon jättipottistrategian pelaamisen täsmälleen 7 281,8 kolikon jättipotilla, voit odottaa voittoasi 201,18 panostuksella. Jos kuitenkin käytit aikaa strategian muutosten oppimiseen 7 281,8 kolikon jättipotissa, odotettu voittosi olisi 234,31 kolikkoa.
Aiheeseen liittyen, luin juuri Frank Kneelandin teoksen The Secret World of Video Poker Progressives . Tässä kirjassa on paljon kaavoja paljon monimutkaisempiin progressiivisiin tilanteisiin, sekä käytännön neuvoja ja tarinoita, jotka perustuvat hänen vuosiinsa progressiivisten pokereiden metsästäjien tiimin vetämisessä. Suosittelen sitä kaikille progressiivisten pokereiden pelaajille.
Oklahomassa sijaitseva kasino laittaa kolme jokeria kuuden pakan blackjack-kenkään. Miten se vaikuttaa kertoimiin?
Stanford Wong käsittelee blackjackin jokereita kirjassaan Basic Blackjack . Siinä hän sanoo, että jokainen pakassa oleva jokeri on pelaajalle 4,2 % arvoinen. Joten puoli jokeria pakkaa kohden olisi 2,1 %:n arvoinen. Hänen kirjassaan on strategia sille, miksi korttiksi jokeri julistetaan, ottaen huomioon pelaajan muut kortit ja jakajan näkyvän kortin.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Onko olemassa tutkimuksia tai lukuja, jotka kertoisivat yksityiskohtaisesti, kuinka suuri osa Las Vegasin blackjack-peleistä on 6-5 tai muita "karnevaali"tyyppisiä variaatioita?
Syyskuun 2010 Current Blackjack Newsletter -uutiskirjeen mukaan Las Vegasissa oli 2099 blackjack-pöytää. Seuraava taulukko näyttää neljän suurimman variaation määrän.
Blackjackin muunnelmat Las Vegasissa
| Peli | Pöydät | Prosentti |
| 6–5 | 467 | 22,2 % |
| Blackjack-kytkin | 42 | 2,0 % |
| Superhauskaa 21 | 41 | 2,0 % |
| Espanja 21 | 6 | 0,3 % |
| Kokonais | 556 | 26,5 % |
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.


