Kysy velholta #261
Mitkä dynamiikat vaikuttavat jalkapallon kokonaistulosvedonlyöntiin kauden edetessä, sään huonontuessa ja joukkueiden viimeaikaisista suorituksista saatavan tiedon lisääntyessä? Kuinka helppoa (tai vaikeaa) on löytää virheitä viivoista?
Vastatakseni tähän kysymykseen piirsin graafin NFL:n keskimääräisistä pisteistä viikkonumeroittain jokaiselta kaudelta vuosina 1983–2009. Seuraava kaavio näyttää tulokset.
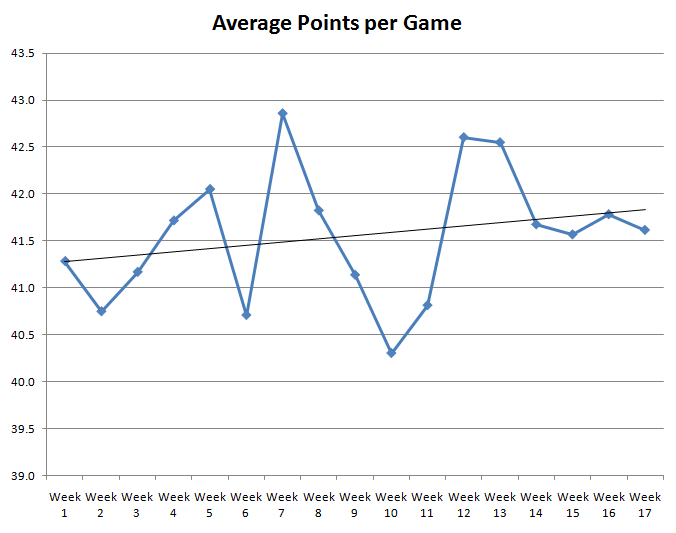
Kuten näette, viiva nousee ja laskee paljon. Ohut musta viiva on pienimmän neliösumman menetelmällä parhaiten sopiva viiva, joka osoittaa yleistä nousevaa trendiä. Vuodenaikojen vaihtuessa ja lämpötilojen laskiessa keskimääräinen pistemäärä kasvaa hieman, mutta se voi hyvinkin olla satunnaista vaihtelua.
Se on suunnilleen niin pitkälle kuin pystyn viemään. Saadakseni yleisen mielipiteen siitä, miten sää vaikuttaa urheiluvedonlyöntiin yleisesti, käännyin ystäväni Jason Beenin puoleen, joka on aiheen asiantuntija. Tässä on mitä hän sanoi:
Useimmissa tapauksissa tuuli on peliin eniten vaikuttava säätekijä, mutta se ei ole ainoa. Baseballissa ja muissa ulkourheilulajeissa varjoilla voi olla yhtä suuri vaikutus, erityisesti kauden alku- ja loppupuolella pelattaviin baseball-iltapäivisin pelattaviin otteluihin. Sade tai lumi ei ole niin suuri tekijä kuin useimmat ihmiset luulevat jalkapallossa, koska se yleensä vaikuttaa sekä hyökkäykseen että puolustukseen tasaisesti. Esimerkkinä tästä olisi puolustuksen takakenttä laitahyökkääjää vastaan. Sade ja lumi hidastaisivat heitä tasaisesti, jolloin kummallakaan osapuolella ei olisi etua. Tuuli voi yksinkertaisesti estää syöttöpelin ja potkupelit jalkapallossa. Olen nähnyt pelejä, joissa syöttöjoukkue on joutunut juoksemaan palloa lähes joka tilanteessa voimakkaan sivutuulen vuoksi. Sitä ei tapahdu usein, mutta joskus tuuli on pelin lopullinen ratkaiseva tekijä.Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Mitä yleensä tapahtuu crapsissa, jos pelaaja panostaa kertoimia moninkertaisesti suuremman panoksen, eivätkä jakajat huomaa sitä ennen kuin panos voittaa tai häviää?
Kysyin tästä entiseltä Vegasin pöytäpelien pelinjohtajalta. Hän sanoi, että kerroinpanoksen osuus, joka ylittää linjapanoksen sallitun kerrannaisen, maksettaisiin place-vedon kertoimien mukaisesti. Tämä kysymys nostettiin esiin ja sitä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Mikä on keskimäärin todennäköisyys NFL:ssä sille, että vastustajajoukkue tekee maalin seuraavana maalin maalin jälkeen?
NFL-kausien 2000–2009 perusteella vastaus on 57 %.
Tarkastellaan kolmen osapuolen kaksintaistelua, jossa osallistujat A, B ja C taistelevat kuolemaan asti naisesta. He ovat kaikki herrasmiehiä ja sopivat seuraavista säännöistä.
- Kolme osallistujaa muodostavat kolmion.
- Jokaisessa on vain yksi luoti.
- A menee ensin, sitten B ja C.
- A:n todennäköisyys osua aiottuun kohteeseen on 10 %.
- B:n todennäköisyys osua aiottuun kohteeseen on 60 %.
- C:n todennäköisyys osua aiottuun kohteeseen on 90 %.
- Vahingossa tapahtuneita ampumisia ei ole.
- Ilmaan ampuminen (tahallisesti ohi) ja itsensä ampuminen on sallittua, ja ne onnistuvat aina.
- Jos kierroksen jälkeen on jäljellä kaksi tai kolme eloonjäänyttä, jokaiselle annetaan uusi luoti. Sen jälkeen he ampuvat vuorotellen samassa järjestyksessä ohittaen kaikki jo kuolleet.
- Kaikki kolme osallistujaa ovat täydellisiä loogikoita.
Kehen A:n tulisi aluksi tähdätä? Mikä on hänen selviytymistodennäköisyytensä kullakin alkuperäisellä kohteella?
Tätä pulmaa käsitellään BBC:n ohjelmassa Quite Interesting . Vieritä 100 riviä alaspäin nähdäksesi vastauksen ja ratkaisun.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
Tässä ovat A:n voittotodennäköisyyteni kunkin alkuperäisen kohteen mukaan. Kuten näette, A:n voittotodennäköisyys maksimoidaan ampumalla tarkoituksella ilmaan.
Truel-kertoimet
| Strategia | Todennäköinen voitto |
| Ilma | 13,887 % |
| A | 0,000 % |
| B | 12,560 % |
| C | 13,094 % |
Ratkaisussa käytetään merkintää Pr(X) merkitsemään todennäköisyyttä, että ryhmä X ja vain ryhmä X on jäljellä kierroksen jälkeen. Käytetään terminologiaa Pr(X*) merkitsemään todennäköisyyttä, että ryhmä X lopulta voittaa kierroksen toistettuaan, kunnes pelin tila muuttuu jonkun osuman vuoksi. Olkoon Pr(X**) todennäköisyys, että pelaaja X on ainoa selviytyjä. Lopullisten todennäköisyyksien löytämiseksi tarkastellaan ensin kahden pelaajan tiloja. On selvää, että molemmat ampuvat toisiaan kohti.
A vastaan B
- Pr(A) = 0,1
- Pr(B) = 0,9 × 0,6 = 0,54
- Pr(AB) = 0,9 × 0,4 = 0,36
Jos molemmat selviävät, he toistavat, kunnes jäljellä on vain yksi. Joten viimeisen selviytyjän todennäköisyydet ovat:
- Pr(A*) = Pr(A)/(1-Pr(AB)) = 0,1/0,64 = 0,15625
- Pr(B*) = Pr(B)/(1-Pr(AB)) = 0,54/0,64 = 0,84375
A vs. C
- Pr(A) = 0,1
- Pr(C) = 0,9 × 0,9 = 0,81
- Pr(AC) = 0,9 × 0,1 = 0,09
Jos molemmat selviävät, he toistavat, kunnes jäljellä on vain yksi. Joten viimeisen selviytyjän todennäköisyydet ovat:
- Pr(A*) = Pr(A)/(1-Pr(AC)) = 0,1/0,91 = 0,10989011
- Pr(C*) = Pr(B)/(1-Pr(AC)) = 0,81/0,91 = 0,89010989
B vs. C
- Pr(B) = 0,6
- Pr(C) = 0,4 × 0,9 = 0,36
- Pr(BC) = 0,$×0,1 = 0,04
Jos molemmat selviävät, he toistavat, kunnes jäljellä on vain yksi. Joten viimeisen selviytyjän todennäköisyydet ovat:
- Pr(B*) = Pr(A)/(1-Pr(BC)) = 0,6/,96 = 0,625
- Pr(C*) = Pr(B)/(1-Pr(BC)) = 0,36/,96 = 0,375
Nyt olemme valmiita analysoimaan kolmen pelaajan tapausta. Tarkastellaan tilannetta, jossa A tähtää B:hen.
Kolme pelaajaa — A tähtää B:hen
Jos A osuu B:hen, C selviää varmasti hengissä ja saattaa osua A:han tai olla osumatta. B:n osumisesta on siis kaksi mahdollista lopputulosta: AC ja C. Jos A osuu ohi B:n, B tähtää suurempaan uhkaan C. Jos B osuu C:hen, A ja B selviävät. Jos B osuu C:hen, C tähtää suurempaan uhkaan B. Jos C osuu B:hen, kaikki kolme selviävät. Jos C osuu B:hen, A ja C selviävät. Mahdolliset lopputulokset ovat C, AB, AC ja ABC.
- Pr(A) = 0.
- Pr(B) = 0.
- Pr(C) = 0,1 × 0,9 = 0,09. Tämä saavutetaan, kun A osuu B:hen ja sitten C osuu A:han.
- Pr(AB) = 0,9 × 0,6 = 0,54. Tämä saavutetaan, kun A osuu B:hen ohi ja sitten B osuu C:hen.
- Pr(AC) = 0,1 × 0,1 + 0,9 × 0,4 × 0,9 = 0,334. Tämä voidaan saavuttaa kahdella tavalla. Ensimmäinen on, että A osuu B:hen ja sitten C ohittaa A:n. Toinen on, että A ohittaa B:n, B ohittaa C:n ja sitten C osuu B:hen.
- Pr(BC) = 0.
- Pr(ABC) = 0,9 × 0,4 × 0,1 = 0,036. Tämä saavutetaan, kun kaikki kolme puuttuvat.
Samalla logiikalla kuin kahden pelaajan tapauksissa, voimme jakaa jokaisen lopputuloksen luvulla (1-Pr(ABC))=0.964 löytääksemme kunkin tilan todennäköisyydet olettaen, että pelin tila muuttui kierroksen jälkeen.
- Pr(C*) = 0,09/0,964 = 0,093361.
- Pr(AB*) = 0,54/0,964 = 0,560166.
- Pr(AC*) = 0,334/0,964 = 0,346473.
Kahden pelaajan tapauksista tiedämme, että jos ratkaisuksi jäävät A ja B, A voittaa todennäköisyydellä 0,15625 ja B 0,84375. Jos ratkaisuksi jäävät A ja C, A voittaa todennäköisyydellä 0,109890 ja C 0,890110.
- Pr(A**) = (0,560165975 × 0,15625) + (0,346473029 × 0,10989011) = 0,125600. A voi olla voittaja kahdella tavalla: (1) pääsemällä AB-tilaan ja voittamalla sitten tai (2) pääsemällä AC-tilaan ja voittamalla sitten.
- Pr(B**) = 0,560166 × 0,84375 = 0,472640. B voittaa, jos se pääsee AB-tilaan, ja silloin B voittaa.
- Pr(C**) = 0,093361 + (0,346473 × 0,890110) = 0,401760. C voi voittaa joko tappamalla A:n ja sitten C tappamalla A:n ensimmäisellä kierroksella tai pääsemällä tilaan AC ja sitten C voittamalla.
Jos A:n strategiana on siis tähtäillä ensin B:hen, hänen todennäköisyytensä olla ainoa selviytyjä on 12,56 %.
Kolme pelaajaa — A tähtää C:hen
Jos A osuu C:hen, B selviää varmasti hengissä ja saattaa osua A:han tai olla osumatta. C:n osumisen kaksi mahdollista lopputulosta ovat AB ja B. Jos A osuu C:hen ohi, B tähtää suurempaan uhkaan C. Jos B osuu C:hen, A ja B selviävät. Jos B osuu C:hen ohi, C tähtää suurempaan uhkaan B. Jos C osuu B:hen, kaikki kolme selviävät. Jos C osuu B:hen, A ja C selviävät. Mahdolliset lopputulokset ovat siis B, AB, AC ja ABC.
- Pr(A) = 0.
- Pr(B) = 0,1 × 0,6 = 0,06.
- Pr(C) = 0.
- Pr(AB) = (0,1 × 0,4) + (0,9 × 0,6) = 0,04 + 0,54 = 0,58. Tämä voidaan saavuttaa kahdella tavalla.Ensimmäinen on A:n osuma C:hen ja sitten B:n A ohitus. Toinen on A:n B ohitus ja sitten B:n C-osuma.
- Pr(AC) = 0,9 × 0,4 × 0,9 = 0,324. Tämä saavutetaan, kun A osuu C:hen, B osuu C:hen ja C osuu B:hen.
- Pr(BC) = 0.
- Pr(ABC) = 0,9 × 0,4 × 0,1 = 0,036. Tämä saavutetaan, kun kaikki kolme puuttuvat.
Samalla logiikalla kuin kahden pelaajan tapauksissa, voimme jakaa jokaisen lopputuloksen luvulla (1-Pr(ABC))=0.964 löytääksemme kunkin tilan todennäköisyydet olettaen, että pelin tila muuttui kierroksen jälkeen.
- Pr(B*) = 0,06/0,964 = 0,062241.
- Pr(AB*) = 0,58/0,964 = 0,601660.
- Pr(AC*) = 0,324/0,964 = 0,336100.
Samalla logiikalla kuin A:n ratkaisu pyrkii B:hen:
- Pr(A**) = (0,601660 × 0,15625) + (0,336100 × 0,10989011) = 0,130943.
- Pr(B**) = 0,062241 + 0,601660 × 0,84375 = 0,569891.
- Pr(C**) = 0,336100 × 0,890110 = 0,299166.
Jos siis A:n strategiana on tähtäillä ensin C:hen, hänen todennäköisyytensä olla ainoa selviytyjä on 13,09 %.
Kolme pelaajaa – A heittää tahallaan ohi
Kun A osuu tahallaan ohi, B tähtää suurempaa uhkaa C:tä kohden. Jos B osuu C:hen, sekä A että B selviävät. Jos B osuu C:hen, C tähtää suurempaa uhkaa B:tä kohden. Jos C osuu B:hen, kaikki kolme selviävät. Jos C osuu B:hen, sekä A että C selviävät. Mahdolliset lopputulokset ovat AB, AC ja ABC.
- Pr(A) = 0.
- Pr(B) = 0.
- Pr(C) = 0.
- Pr(AB) = 0,6. Tämä saavutetaan, kun B osuu C:hen.
- Pr(AC) = 0,4 × 0,9 = 0,36. Tämä saavutetaan, kun B osuu C:hen ja sitten C osuu B:hen.
- Pr(BC) = 0.
- Pr(ABC) = 0,4 × 0,1 = 0,04. Tämä saavutetaan, kun kaikki kolme puuttuvat.
Samalla logiikalla kuin kahden pelaajan tapauksissa, voimme jakaa jokaisen lopputuloksen luvulla (1-Pr(ABC))=0.96 löytääksemme kunkin tilan todennäköisyydet olettaen, että pelin tila muuttui kierroksen jälkeen.
- Pr(AB*) = 0,6/0,96 = 0,625.
- Pr(AC*) = 0,36/0,96 = 0,375.
Samalla logiikalla kuin A:n ratkaisu pyrkii B:hen:
- Pr(A**) = (0,625 × 0,15625) + (0,375 × 0,109890) = 0,138865.
- Pr(B**) = 0,625 × 0,84375 = 0,527344.
- Pr(C**) = 0,375 × 0,890110 = 0,333791.
Jos siis A:n strategiana on tähtäillä ensin C:hen, hänen todennäköisyytensä olla ainoa selviytyjä on 13,89 %.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.


