Kysy velholta #265

Sekoitat keskiarvon ja mediaanin. Katsotaanpa esimerkkinä minun tilannettani. Olen 45-vuotias mies. Elinajanodotteeni on 78,11 vuotta, mutta minulla on 50,04 %:n mahdollisuus elää 80-vuotiaaksi.

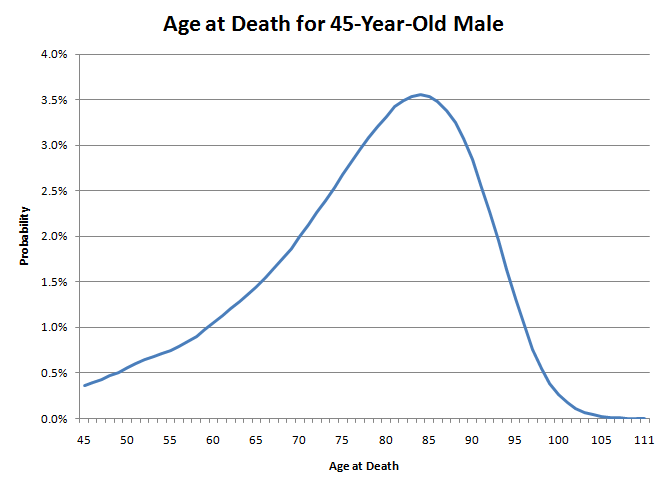
Kuolinikäni on kuin heittäisi tikanheittoa tähän käyrään. Huomaa, kuinka vasen häntä on paljon lihavampi kuin oikea. Tämä tarkoittaa, että kuolemani todennäköisyys juuri nyt on melko pieni. Vanhetessani kuoleman todennäköisyys seuraavana vuonna kuitenkin kasvaa jatkuvasti. Esimerkiksi 45-vuotiaalla miehellä todennäköisyys selvitä 46-vuotiaaksi on melko korkea, 99,64 %. Kuitenkin 85-vuotiaana todennäköisyys selvitä 86-vuotiaaksi on vain 89,21 %. Se on kuin luonto työntäisi hitaasti veistä selkään. Aluksi se ei luultavasti tapa sinua, mutta joka vuosi todennäköisyys sille kasvaa hitaasti. Kuitenkin, kun pääset 70-luvun lopulle, luonto sanoo, että riittää peleillä, ja alkaa todella tunkeutua peliin.

Jos siis paljon 45-vuotiaita miehiä heittää tikkaa tähän kaavioon, 49,96 % osuu 45–79-vuotiaisiin ja 50,04 % 80–111-vuotiaisiin. Onnekas puolisko, joka pääsee kaavion oikealle puolelle, ei kuitenkaan todennäköisesti elä paljon yli 80 vuoden iän. Kun mies täyttää 80 vuotta, hän voi odottaa elävänsä vain 7,78 vuotta pidempään. Samaan aikaan monet epäonnisesta puoliskosta, jotka eivät elä 80 ikävuoteen, kuolevat paljon nuorempina. Joten juuri monet nuoret kuolemat laskevat keskimääräistä elinajanodotetta.

Samankaltaisessa tilanteessa tarkastellaan noppaa, jonka numerot ovat 10, 20, 30, 31, 32, 33. Keskiarvo on 26, mutta on 2/3 mahdollisuus saada enemmän.

Esimerkkinä keskiarvon ja mediaanin eroista oletetaan, että lisäämme otokseen kaksi kuolemantapausta lisää. Yksi kuolema 46-vuotiaana ja yksi 81-vuotiaana. Todennäköisyys selvitä 80-vuotiaaksi ei muutu, mutta keskimääräinen elinajanodote 45-vuotiaana lyhenisi.

Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.

Hyvä kysymys. Talon strategian mukaan viisi ässää pitää jakaa ja kaksi ässää pelataan matalalla kädellä. Poikkeuksena on pitää viitoset korkealla kädellä, jos pystyy pelaamaan kaksi kuningasta matalalla kädellä. Pai Gow -pokerisivuni kertoo seitsemän talon strategiaa Las Vegasista ja Atlantic Citystä, ja ne kaikki sisältävät tämän poikkeuksen. Näiden kahden kaupungin ulkopuolelta tulevat kolmoset eivät sisällä tätä poikkeusta.

Todennäköisyys saada neljä ässää, jokeri ja kaksi kuningasta on 1/25 690 513. Olettaen, että jakaja panostaa, ainoa tilanne, jossa tästä poikkeuksesta olisi apua, on jos pelaajalla olisi neloset tai parempi korkeassa kädessä. Tämän todennäköisyys on noin 1/300. Molempien todennäköisyys on noin 1/7,6 miljardia.

Nevadan pelivalvontalautakunnan mukaan Nevadassa oli vuonna 2009 306 pai gow -pokeripöytää. Jos oletamme rehellisesti, että jakoja pelataan 60 kertaa tunnissa, kaksi pelaajaa pöytää kohden ja jokainen pöytä on auki 24/7, niin tämän poikkeuksen ilmeneminen ja lopputuloksen muuttaminen kestäisi 23,7 vuotta.

Joten kasinot vaativat jokaista pai gow -pokerin jakajaa muistamaan tämän poikkeuksen, vaikka sillä ei ehkä ole koskaan ollut merkitystä pelin historiassa. Arvelen, että sama henkilö, joka keksi lisätä kyseisen säännön, oli sama henkilö, joka päätti, että A2345-suora, joka tunnetaan nimellä "pyörä", on toiseksi korkein suora.

Tämä on klassinen ongelma todennäköisyyslaskennan historiassa. Monet ihmiset virheellisesti luulevat vastauksen olevan 18, koska luvun 12 todennäköisyys on 1/36 ja 18 × (1/36) = 50 %. Tämän logiikan mukaan luvun 12 todennäköisyys 36 heitolla olisi kuitenkin 100 %, mikä se ei selvästikään ole. Tässä on oikea ratkaisu. Olkoon r heittojen lukumäärä. Todennäköisyys sille, että heitto ei ole 12, on 35/36. Todennäköisyys, että r heitolla on 0 12:ta, on (35/36) ^r . Joten meidän on ratkaistava r seuraavassa yhtälössä:

(35/36) ^r = 0,5
log(35/36) ^r = log(0,5)
r × log(35/36) = log(0,5)
r = log(0,5)/log(35/36)
r = 24,6051

Joten pyöreää vastausta ei ole. Todennäköisyys saada 12 24 heitolla on 1-(35/36) ²⁴ = 49,14 %. Todennäköisyys saada 12 25 heitolla on 1-(35/36) ²⁵ = 50,55 %.

Jos haluat lyödä vetoa tästä, sanotaan, että saat 25 heitolla tulokseksi 12 tai joku muu ei saa sitä 24 heitolla. Kummassakin tapauksessa sinulla on etulyöntiasema tasatilanteessa.

Lyön vetoa kymmenen yhteen, että saat rahasi, vaikka he saattavat ensin keskustella kanssasi muutaman sanan. Epäilen asiaa siksi, että vedonlyöntitoimisto voi peruuttaa ilmeisen virheellisesti tehdyn vedon pelivalvontalautakunnan luvalla.

"Vedonlyöntiyhtiö ei voi yksipuolisesti peruuttaa mitään vetoa ilman puheenjohtajan etukäteen antamaa kirjallista suostumusta." -- Nevadan asetus 22.115

Vaikka tämä oikeus on olemassa kokemusperäisten todisteiden perusteella, sitä käytetään hyvin harvoin. Kerro minulle, mitä tapahtuu.

ps Kysyjä ilmoitti minulle myöhemmin, että hänelle maksettiin ilman suurempia ongelmia.

Kyllä, se tulee olemaan, ^{100 000} -1 sekunnin kuluttua. Katso mathproblems.info -sivustoltani tehtävästä 206 kaksi ratkaisua.

Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.