Kysy velholta #267
Mikä olisi optimaalinen strategia rahojesi jakamiseen Million Dollar Money Drop -peliohjelmassa, jos et ole varma vastauksesta?
Muiden lukijoiden hyödyksi, haluan ensin tarkistaa säännöt.
- Pelaajajoukkue aloittaa 1 000 000 dollarilla.
- Joukkueelle annetaan monivalintakysymys.
- Joukkueen on jaettava rahansa mahdollisten vastausten kesken. Oikeaan vastaukseen panostettu raha siirtyy seuraavaan kysymykseen.
- Joukkueen on suljettava kokonaan pois ainakin yksi mahdollinen vastaus olemalla panostamatta siihen rahaa.
- Tämä prosessi toistuu useiden kierrosten ajan. Pelaajalle annetaan myös yksi mahdollisuus muuttaa mieltään.
Jos joukkue on varma vastauksesta, hänen tulisi tietenkin panostaa kaikki rahansa oikeaan vastaukseen. Jos joukkue pystyy rajaamaan vastauksen kahteen, mutta antaa kummallekin 50 %:n todennäköisyyden olla oikea, heidän tulisi jakaa rahansa tasan kahden vaihtoehdon kesken.
Vaikeammaksi tilanne muuttuu, jos joukkue kallistuu yhden vastauksen puoleen, mutta ei sulje täysin pois yhtä tai useampaa muuta. Katsotaanpa esimerkkiä. Oletetaan, että joukkue määrittää kunkin oikean vastauksen todennäköisyyden seuraavasti: A 10 %, B 20 %, C 30 %, D 40 %. Miten heidän tulisi jakaa hänen rahansa?
Väitän, että vastaus on noudattaa Kellyn kaavaa . Lyhyesti sanottuna joukkueen tulisi maksimoida hänen varallisuutensa logaritmi jokaisella kysymyksellä. Tätä varten sinun on otettava huomioon, kuinka paljon varallisuutta sinulla jo on.
Oletetaan, että nykyinen varallisuutesi, jonka olet kerännyt ohjelmasta riippumatta, on 100 000 dollaria. Tämä on ensimmäinen kysymyksesi, joten sinulla on 1 000 000 dollaria ohjelmarahaa jaettavana. Ensin poista vaihtoehto, jolla on pienin todennäköisyys, ohjelman sääntöjen mukaisesti. Sitten haluat maksimoida 0,2 × log(100 000 + b * 1 000 000) + 0,3 × log(100 000 + c * 1 000 000) + 0,4 × log(100 000 + d * 1 000 000), jossa pienet a, b ja c viittaavat kunkin vastauksen osuuteen.
Tämä voitaisiin ratkaista differentiaali- ja integraalilaskennalla ja ratkaisemalla trinomiyhtälö, kokeilemalla ja erehtymällä tai mieluummin Excelin "tavoitteen etsintä" -toiminnolla. Käytitpä mitä tahansa menetelmää, oikea vastaus on laittaa 18,9 % B:hen, 33,3 % C:hen ja 47,8 % D:hen.
Tietenkään kukaan ohjelmassa ei pysty tekemään kaikkea tätä matematiikkaa annetussa ajassa, puhumattakaan siitä, että sinun on myös siirrettävä paljon käteistä tuona aikana. Käytännöllisempi neuvoni on jakaa rahat suhteessa vastauksen todennäköisyyden arvioosi olettaen, että epätodennäköisin vaihtoehto ei ole mahdollinen. Esimerkissä tämä johtaisi 22,2 %:n jakautumiseen B:lle, 33,3 %:n jakautumiseen C:lle ja 44,4 %:n jakautumiseen D:lle.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
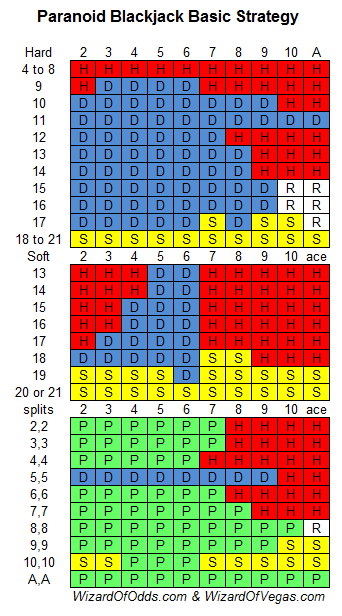
Kuulin kasinosta, jossa jakaja olettaa kaikkien jäljellä olevien pelaajien voittaneen, jos hän häviää. Peli jaetaan kuvapuoli ylöspäin, paitsi että tuplauskortit jaetaan kuvapuoli alaspäin. Joten jos tuplauskortti aiheuttaa pelaajan häviämisen, mutta jakajakin häviää, pelaaja voittaa. Kasino tekee näin, koska se on vainoharhainen korttienlaskijoiden suhteen eikä halua pelaajien näkevän kortteja, joita he pitävät merkityksettöminä. Mikä olisi oikea perusstrategia tämän säännön ja talon edun vallitessa?
Oletan, että pakkaa on kuusi, jakaja saa pehmeän 17, tuplataan jaon jälkeen, luovutetaan ja ässät jaetaan uudelleen. Jos tuplaaminen vähemmällä ei ole sallittua, pelaajan etu on 4,9 %. Tässä on oikea strategia. Tämä strategia voi tietenkin laukaista joitakin varoitusmerkkejä.
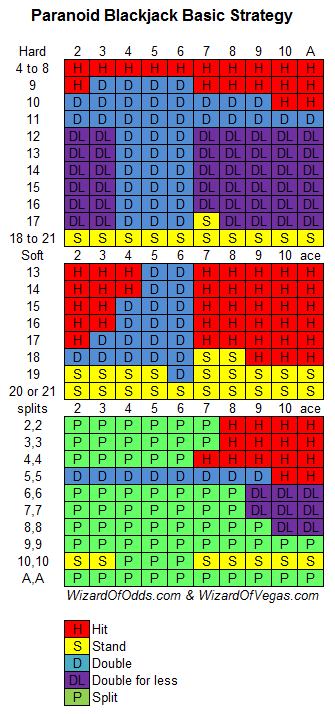
Jos tuplaaminen vähemmällä panoksella on sallittua, saan seuraavalla strategialla pelaajan edun olevan enintään 9,4 %. Kun tuplaat vähemmällä panoksella, panosta mahdollisimman vähän ylimääräistä, mieluiten vain yhden pennin. 9,4 %:n lukuni olettaa pienen tuplauspanoksen. Todellisuudessa useimmat kasinot vaativat tuplaamisen vähintään pöydän minimipanoksella.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Casino Viennassa blackjackissa on sivupanos. Pelissä käytetään kuutta pakkaa ja jakaja jää pehmeälle 17:lle. Jos jakaja häviää, voittosuhde on 5:2 alkuperäisen panoksen tuloksesta riippumatta.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Mielenkiintoista. Kuten kirjoitin, arvioin tuon käden tapahtuvan noin kerran 23,7 vuodessa missä tahansa Nevadassa. Sanoisin, että se oli yksi niistä ajoista.


