Kysy velholta #284
Kuulitko Seattlen autoliikkeestä, jonka piti maksaa 420 000 dollaria, koska Seahawks voitti Giantsin nollapelin? Luin, että heidän piti maksaa 7 000 dollaria vakuutuksesta sitä varten. Mikä olisi ollut kohtuullinen vakuutusmaksu?
Artikkelin mukaan Washingtonin autoliike maksoi 420 000 dollaria Seahawksin nollapelin jälkeen , autoliike järjesti kampanjan, jossa kahdelletoista voittajalle maksettiin 35 000 dollaria kullekin, jos Seahawks voitti Giants-ottelun viikolla 15, joka pelattiin 15. joulukuuta 2013. Artikkelissa todetaan edelleen, että autoliike maksoi 7 000 dollaria vakuutuksesta, jolla katettaisiin kyseisen tapahtuman varalta.
Jokaisen NFL-ottelun perusteella kausilta 1983-2012, tietty joukkue missä tahansa ottelussa nollattiin. Koska olen kuitenkin seitsemän pisteen altavastaaja ottelussa, jossa keskimääräinen yli/alle-luku on, väittäisin, että Giantsin nollapelin todennäköisyys oli keskimääräistä suurempi. Yli/alle-luku kyseisessä ottelussa oli 41. Tehdäänpä hieman algebraa ratkaistaksemme Giantsin pisteiden odotusarvon.
Olkoon:
s=Seahawks-pisteet
g=Giantsin pisteet
Tiedämme, että s+g=41 ja s=g+7, piste-erosta ja yli/alle-summasta riippuen.
Sijoittamalla toinen yhtälö ensimmäiseen:
(g+7) + g = 41
2 g + 7 = 41
2 g = 34
g = 17
Seuraavaksi tarkastellaan nollapelin todennäköisyyttä kunkin joukkueen arvioidun pistemäärän perusteella kausien 1983–2012 perusteella. Ohitin rivit, joissa otoskoko oli nolla.
Nollapelin todennäköisyys
| Arvioitu Pisteet | Otoksen koko | Nollapelit | Suhde |
|---|---|---|---|
| 5.25 | 1 | 0 | 0,0 % |
| 6.50 | 1 | 0 | 0,0 % |
| 7.75 | 1 | 0 | 0,0 % |
| 8.00 | 1 | 0 | 0,0 % |
| 8.25 | 3 | 0 | 0,0 % |
| 8.50 | 2 | 0 | 0,0 % |
| 8.75 | 2 | 0 | 0,0 % |
| 9.00 | 2 | 0 | 0,0 % |
| 9.50 | 4 | 0 | 0,0 % |
| 9.75 | 6 | 1 | 16,7 % |
| 10.00 | 10 | 1 | 10,0 % |
| 10.25 | 7 | 0 | 0,0 % |
| 10.50 | 14 | 2 | 14,3 % |
| 10.75 | 7 | 1 | 14,3 % |
| 11.00 | 13 | 1 | 7,7 % |
| 11.25 | 21 | 1 | 4,8 % |
| 11.50 | 22 | 3 | 13,6 % |
| 11.75 | 23 | 1 | 4,3 % |
| 12.00 | 34 | 2 | 5,9 % |
| 12.25 | 36 | 7 | 19,4 % |
| 12.50 | 41 | 3 | 7,3 % |
| 12.75 | 39 | 4 | 10,3 % |
| 13.00 | 55 | 1 | 1,8 % |
| 13.25 | 58 | 5 | 8,6 % |
| 13.50 | 78 | 1 | 1,3 % |
| 13.75 | 89 | 5 | 5,6 % |
| 14.00 | 92 | 4 | 4,3 % |
| 14.25 | 108 | 7 | 6,5 % |
| 14.50 | 117 | 8 | 6,8 % |
| 14.75 | 141 | 7 | 5,0 % |
| 15.00 | 160 | 7 | 4,4 % |
| 15.25 | 160 | 7 | 4,4 % |
| 15.50 | 213 | 7 | 3,3 % |
| 15.75 | 198 | 11 | 5,6 % |
| 16.00 | 206 | 6 | 2,9 % |
| 16.25 | 221 | 12 | 5,4 % |
| 16.50 | 241 | 10 | 4,1 % |
| 16.75 | 273 | 7 | 2,6 % |
| 17.00 | 306 | 8 | 2,6 % |
| 17.25 | 305 | 8 | 2,6 % |
| 17.50 | 306 | 10 | 3,3 % |
| 17.75 | 323 | 4 | 1,2 % |
| 18.00 | 299 | 8 | 2,7 % |
| 18.25 | 332 | 8 | 2,4 % |
| 18.50 | 309 | 9 | 2,9 % |
| 18.75 | 307 | 7 | 2,3 % |
| 19.00 | 356 | 8 | 2,2 % |
| 19.25 | 389 | 5 | 1,3 % |
| 19.50 | 361 | 5 | 1,4 % |
| 19,75 | 343 | 6 | 1,7 % |
| 20.00 | 402 | 8 | 2,0 % |
| 20.25 | 379 | 6 | 1,6 % |
| 20,50 | 359 | 3 | 0,8 % |
| 20.75 | 353 | 5 | 1,4 % |
| 21.00 | 344 | 1 | 0,3 % |
| 21.25 | 317 | 3 | 0,9 % |
| 21.50 | 341 | 2 | 0,6 % |
| 21.75 | 331 | 1 | 0,3 % |
| 22.00 | 369 | 1 | 0,3 % |
| 22.25 | 336 | 0 | 0,0 % |
| 22.50 | 316 | 2 | 0,6 % |
| 22.75 | 280 | 3 | 1,1 % |
| 23.00 | 311 | 1 | 0,3 % |
| 23.25 | 290 | 3 | 1,0 % |
| 23.50 | 279 | 1 | 0,4 % |
| 23.75 | 255 | 1 | 0,4 % |
| 24.00 | 246 | 1 | 0,4 % |
| 24.25 | 219 | 0 | 0,0 % |
| 24,50 | 230 | 2 | 0,9 % |
| 24,75 | 230 | 1 | 0,4 % |
| 25,00 | 212 | 2 | 0,9 % |
| 25.25 | 207 | 0 | 0,0 % |
| 25,50 | 176 | 1 | 0,6 % |
| 25,75 | 154 | 0 | 0,0 % |
| 26.00 | 154 | 1 | 0,6 % |
| 26.25 | 113 | 0 | 0,0 % |
| 26,50 | 137 | 0 | 0,0 % |
| 26,75 | 122 | 0 | 0,0 % |
| 27.00 | 95 | 0 | 0,0 % |
| 27.25 | 98 | 0 | 0,0 % |
| 27,50 | 83 | 0 | 0,0 % |
| 27,75 | 81 | 0 | 0,0 % |
| 28.00 | 82 | 0 | 0,0 % |
| 28.25 | 55 | 1 | 1,8 % |
| 28,50 | 56 | 0 | 0,0 % |
| 28,75 | 51 | 0 | 0,0 % |
| 29,00 | 48 | 0 | 0,0 % |
| 29.25 | 34 | 0 | 0,0 % |
| 29,50 | 24 | 0 | 0,0 % |
| 29,75 | 25 | 0 | 0,0 % |
| 30,00 | 24 | 0 | 0,0 % |
| 30.25 | 21 | 0 | 0,0 % |
| 30,50 | 18 | 0 | 0,0 % |
| 30,75 | 23 | 0 | 0,0 % |
| 31,00 | 16 | 0 | 0,0 % |
| 31.25 | 15 | 0 | 0,0 % |
| 31,50 | 8 | 0 | 0,0 % |
| 31,75 | 3 | 0 | 0,0 % |
| 32,00 | 6 | 0 | 0,0 % |
| 32.25 | 7 | 0 | 0,0 % |
| 32,50 | 6 | 0 | 0,0 % |
| 32,75 | 3 | 0 | 0,0 % |
| 33,00 | 4 | 0 | 0,0 % |
| 33.25 | 6 | 0 | 0,0 % |
| 33,50 | 5 | 0 | 0,0 % |
| 34,75 | 4 | 0 | 0,0 % |
| 35,00 | 2 | 0 | 0,0 % |
| 35,50 | 1 | 0 | 0,0 % |
| 36,00 | 2 | 0 | 0,0 % |
| 36.25 | 1 | 0 | 0,0 % |
| 36,50 | 1 | 0 | 0,0 % |
| 37.25 | 1 | 0 | 0,0 % |
| 37,75 | 2 | 0 | 0,0 % |
| 42.25 | 1 | 0 | 0,0 % |
Seuraavat vaiheet ovat liian monimutkaisia selitettäviksi tässä, mutta kehitin kaavan nollapelin todennäköisyydelle, kun otetaan huomioon arvioitujen pisteiden määrä.
p = Arvioidut pisteet.
x = 1,562545 -0,302485 * p
nollapelin todennäköisyys = e x /(1 + e x )
Seuraava kaavio näyttää nollapelin todellisen ja arvioidun todennäköisyyden 14–22 pisteen sarjassa.
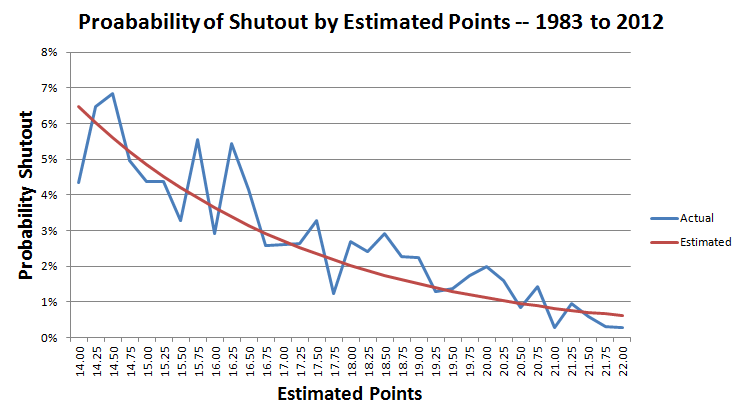
Kyseisessä ottelussa Giants odotti tekevänsä 17 pistettä.
Käyttämällä taulukon yläpuolella olevaa kaavaa:
x = 1,562545 -0,302485 * 17 = -3,579706
Nollapelin todennäköisyys = exp(-3,579706)/(exp(-3,579706)+1) = 2,71 %. Tarkalleen ottaen 0,0271275.
Koska autoliikkeen olisi pitänyt maksaa 420 000 dollaria Giantsin nollapelin sattuessa, vakuutuksen käypä hinta olisi ollut 420 000 dollaria × 0,0271275 = 11 394 dollaria. Normaalisti vakuutusyhtiöt, jotka vakuuttavat tällaisia epätavallisia kampanjoita, kaksinkertaistavat käyvän hinnan, joten olisin odottanut vakuutusmaksun olevan 22 788 dollaria. Joten autoliikkeen maksama 7 000 dollarin vakuutusmaksu oli huijaus. Olettaen, että pomo tarkistaa laskelmat, en haluaisi olla sen henkilön saappaissa, joka laski tuon 7 000 dollarin vakuutusmaksun.
Tämä kysymys nostettiin esiin ja siitä keskusteltiin foorumillani Wizard of Vegasissa .
Mikä on todiste siitä, ettei suurinta alkulukua ole olemassa?
Oletetaan hetken ajan, että on olemassa suurin alkuluku. Voimme numeroida alkuluvut p1=2, p2=3, p3=5, p4=7, ... pL = suurin alkuluku.
Määritellään nyt luku x = p1*p2*p3*p4*...*pL + 1.
Alkuluku tarkoittaa sitä, ettei mikään muu pienempi alkuluku jakaudu sen kanssa tasan.
Jos jaamme p1:n, p2:n, p3:n, ... pL:n x:llä, saamme joka kerta jakojäännöksen, joka on 1.
Voisit väittää, että ehkä pL:ää suurempi alkuluku jakautuu x:ään tasan. Kyllä, mutta silloin olisit löytänyt suuremman alkuluvun kuin niin kutsuttu suurin alkuluku. Jos ei, niin x:stä tulee uusi suurin alkuluku, mikä todistaa ristiriidan kautta alkuperäisen oletuksen suurimman alkuluvun olemassaolosta.
Tätä kysymystä esitettiin ja siitä keskusteltiin foorumillani Wizard of Vegasissa .
Oletko samaa mieltä Business Insiderin artikkelin "Matematiikka sanoo, että sinun pitäisi ostaa Mega Millions -lippu heti" kanssa?
En ole samaa mieltä. Se on kamalaa journalismia ja Business Insiderin pitäisi hävetä siitä.
Aluksi artikkeli julkaistiin 17. joulukuuta 2013, ennen sinä iltana järjestettyä 636 miljoonan dollarin arvontaa. Tarkastellaanpa matematiikkaa 1 dollarin lipun arvon arvioimiseksi. Seuraava taulukko näyttää kaikkien mahdollisten tulosten todennäköisyydet ja odotetun tuoton 636 miljoonan dollarin jättipotille ennen kuin otetaan huomioon esimerkiksi kertakorvaus, verot ja jättipotin jakaminen. Kolme suurinta todennäköisyyttä ovat tieteellisessä muodossa, koska luvut ovat niin pieniä.
Mega Millions -- 636 miljoonan dollarin jättipotti
| Saalis | Mega-pallo | Maksaa | Yhdistelmät | Todennäköisyys | Palata |
|---|---|---|---|---|---|
| 5 | Kyllä | 636 000 000 dollaria | 1 | 3.86E-09 | 2.456634 |
| 5 | Ei | 1 000 000 dollaria | 14 | 5.41E-08 | 0,054077 |
| 4 | Kyllä | 5 000 dollaria | 350 | 1.35E-06 | 0,006760 |
| 4 | Ei | 500 dollaria | 4 900 | 0.000019 | 0,009463 |
| 3 | Kyllä | 50 dollaria | 24 150 | 0.000093 | 0,004664 |
| 3 | Ei | 5 dollaria | 338 100 | 0,001306 | 0,006530 |
| 2 | Kyllä | 5 dollaria | 547 400 | 0.002114 | 0,010572 |
| 1 | Kyllä | 2 dollaria | 4 584 475 | 0,017708 | 0,035416 |
| 0 | Kyllä | 1 dollari | 12 103 014 | 0,046749 | 0,046749 |
| Häviäjä | 0 dollaria | 241 288 446 | 0.932008 | 0.000000 | |
| Kokonais | 258 890 850 | 1.000000 | 2.630865 | ||
Tämä osoittaa, että yhden dollarin lipusta saa takaisin 2,630864 dollaria. Lipun hinnan vähentämisen jälkeen odotettu voitto on 1,630864 dollaria. Business Insider saa 1,632029 dollaria. Eroa on 0,001164, mutta ei iso juttu.
Kolme asiaa kuitenkin laskee arvoa merkittävästi:
- Kertakorvaus.
- Verot.
- Jackpotin jakaminen.
Katsotaanpa niitä yksi kerrallaan.
Suuret lottovoitot, kuten Mega Millions, maksetaan yleensä noin 30 vuoden annuiteettina. Jos voittaja haluaa rahat kerralla, kuten useimmat haluavat, hänen on otettava merkittävä vähennys. Tämä on vain oikeudenmukaista, koska dollari tänään on arvokkaampi kuin dollari tulevaisuudessa. 17. joulukuuta 2013 arvonnassa kokonaispalkintosumma pieneni 347,6 miljoonaan dollariin eli 54,65 prosenttiin mainostetusta jättipotista.
Seuraavaksi tarkastellaan veroja. Korkein liittovaltion marginaaliveroaste on 39,6 %. Osavaltioiden verot vaihtelevat 0 %:sta 12,3 %:iin, joten sanotaanpa keskimäärin 6 %. Kun veroista vähennetään 45,6 %, jäljelle jää 189,1 miljoonaa dollaria.
Nyt tulee hankalin osuus – jättipottien jakaminen. On huomattava, että 22. lokakuuta 2013 pidetystä arvonnasta alkaen Mega Millions muutti sääntöjä 75-15-muotoon, jossa arvotaan viisi numeroa väliltä 1–75 ja sitten yksi erillisestä numeroiden 1–15 joukosta. Tämä laski voittotodennäköisyyden yhteen 258 890 850:stä, ilmeisesti pyrkimyksenä saada suurempia jättipotteja. Tarkasteltaessa pelkästään 17 arvontaa sen jälkeen ja LottoReport.comin jättipotti- ja myyntitietoja, havaitsin, että jättipotin koon ja kysynnän välillä on eksponentiaalinen suhde. Havaitsin saman asian muuten Powerball- loton yhteydessä. Käyttämällä eksponentiaalista regressiota, myytyjen lippujen kokonaismäärän (miljoonia) kaavani on 12,422 × exp(0,0052 × j), jossa j on jättipotin koko (miljoonia). Esimerkiksi 636 miljoonan dollarin jättipotin odotettu myynti olisi 12,422 * exp(0,0052 * 636) = 339,2 (miljoonaa). Toteutunut myynti oli 337 miljoonaa dollaria, joten melko lähellä.
Toteutuneen 336 545 306 lipunmyynnin perusteella voimme odottaa voittajaksi 336 545 306 / 258 890 850 = 1 300. Olennainen kysymys on, kuinka monen muun ihmisen kanssa voit odottaa jakavasi rahat, jos voitat? Tähän on helppo vastata tarkastelemalla Poisson-jakaumaa. Jos voittajien keskiarvo on 1,3, täsmälleen x voittajan todennäköisyys on exp(1,3) × 1,3 x /fact(x). Seuraava taulukko näyttää 0–10 muun voittajan todennäköisyyden, osuutesi jättipotista kussakin tapauksessa ja odotetun osuuden olettaen, että voitat.
Odotettu jättipottiosuus keskimäärin 1,3 muulle voittajalle
| Muut voittajat | Todennäköisyys | Jackpot-osuus | Odotettu osuus |
|---|---|---|---|
| 10 | 0.000001 | 0,090909 | 0.000000 |
| 9 | 0.000008 | 0.100000 | 0.000001 |
| 8 | 0.000055 | 0.111111 | 0.000006 |
| 7 | 0,000339 | 0,125000 | 0,000042 |
| 6 | 0,001827 | 0.142857 | 0,000261 |
| 5 | 0,008431 | 0,166667 | 0.001405 |
| 4 | 0,032429 | 0,200000 | 0,006486 |
| 3 | 0,099786 | 0,250000 | 0,024946 |
| 2 | 0,230283 | 0,333333 | 0,076761 |
| 1 | 0,354295 | 0,500000 | 0.177148 |
| 0 | 0,272545 | 1.000000 | 0,272545 |
| Kokonais | 1.000000 | 0,559602 |
Oikeassa alakulmassa oleva solu osoittaa, että voit odottaa pitäväsi 55,96 % rahoista ja loput 44,04 % menee niille pirun muille voittajille, joiden kanssa joudut jakamaan ne.
Nyt 636 miljoonan dollarin jättipottimme on laskenut 189,1 dollariin × 55,96 % = 105,8 miljoonaan dollariin. Katsotaanpa, miltä palautustaulukko näyttää, kun tämä luku on jättipotti.
Mega Millions -- 105,8 miljoonan dollarin jättipotti
| Saalis | Mega-pallo | Maksaa | Yhdistelmät | Todennäköisyys | Palata |
|---|---|---|---|---|---|
| 5 | Kyllä | 105 800 000 dollaria | 1 | 3.86E-09 | 0.408666 |
| 5 | Ei | 1 000 000 dollaria | 14 | 5.41E-08 | 0,054077 |
| 4 | Kyllä | 5 000 dollaria | 350 | 1.35E-06 | 0,006760 |
| 4 | Ei | 500 dollaria | 4 900 | 0.000019 | 0,009463 |
| 3 | Kyllä | 50 dollaria | 24 150 | 0.000093 | 0,004664 |
| 3 | Ei | 5 dollaria | 338 100 | 0,001306 | 0,006530 |
| 2 | Kyllä | 5 dollaria | 547 400 | 0.002114 | 0,010572 |
| 1 | Kyllä | 2 dollaria | 4 584 475 | 0,017708 | 0,035416 |
| 0 | Kyllä | 1 dollari | 12 103 014 | 0,046749 | 0,046749 |
| Häviäjä | 0 dollaria | 241 288 446 | 0.932008 | 0.000000 | |
| Kokonais | 258 890 850 | 1.000000 | 0,582898 | ||
Oikeassa alakulmassa oleva solu näyttää odotetun tuoton 58,29 %. Toisin sanoen 1 dollarin sijoituksesi voi odottaa tuovan takaisin noin 58 senttiä, jolloin odotettu tappio eli talon etu on noin 42 %. Kuulostaako tuo siltä, että sinun pitäisi ostaa lippu?
Artikkelin mukaan "niin kauan kuin myytyjä lippuja on alle 730 miljoonaa, mikä on melko todennäköinen tilanne juuri nyt, lipun odotusarvon pitäisi olla positiivinen, joten sinun kannattaa harkita Mega Millions -lipun ostamista tänään."
Myyntiä kertyi paljon vähemmän kuin 730 miljoonaa, ja se oli silti hirvittävä arvo. Artikkelissa kuitenkin todettiin oikeudenmukaisuuden nimissä seuraavaa:
Muista, että tässä analyysissä on monia varauksia. Verot todennäköisesti vaikuttavat odotettuihin voittoihisi melko vakavasti – liittovaltio ottaa noin 40 % ja kotiosavaltiosi vaatii 0–13 %:n verotuksen.
Monet ihmiset ovat ostaneet lippuja, ja kuten edellä mainittiin, tämä lisää huomattavasti tasapelin todennäköisyyttä ja siihen liittyvää pienempää voittoa." – Business Insider
Nuo ovat melko tärkeitä huomioita! Niitä ei pitäisi vain mainita ohimennen lopussa, vaan ne pitäisi ottaa huomioon analyysissä heti alkuunsa.
Ei niin, että kysyit, mutta mielestäni matematiikan mukaan Mega Millionsia ei kannata koskaan pelata. Ottaen huomioon lippujen eksponentiaalisen kysynnän jackpotin koon perusteella, optimaalinen peliaika on mielestäni 545 miljoonan dollarin jackpot. Tätä suuremmilla jackpoteilla joudut jakamaan sen liian monen muun voittajan kanssa. Tuolla jackpotin koolla pelaaja voi odottaa 60,2 %:n tuottoa tai 39,8 %:n tappiota. Se on korkeintaan se, mitä voi olla.
Lopuksi totean, etten ole samaa mieltä Business Insiderin kanssa siitä, että he huijaavat lukijoita sensaatiomaisella otsikolla eivätkä tee kunnollista analyysia veroista ja jättipottien jakamisesta.
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .


