Kysy velholta #307
Osallistun vuoden 2018 "kuolleen altaan" turnaukseen. Tässä ovat säännöt:
- Jokaisen pelaajan on lähetettävä lista kymmenestä elossa olevasta alle 100-vuotiaasta julkkiksesta.
- Jos jokin julkkis kuolee, kuten Associated Pressin maininta osoittaa vuonna 2018, kuka tahansa, jonka nimi on julkkiksen listalla, saa 100-x pistettä, jossa x on kuolinikä.
- Eniten pisteitä 1.1.2019 kerännyt pelaaja voittaa.
Keskiarvoista poiketen, mikä on optimaalinen strategia tälle pelille?
Entisenä aktuaarina kysyit oikealta henkilöltä. Toivottavasti aktuaariyhdistys ei pidä vastaustani ammatin väärinkäytönä. Vastatakseni kysymykseesi tutustuin kuitenkin vuoden 2014 elinaikataulukkoon entisestä työpaikastani, Sosiaaliturvaviranomaisen pääaktuaarin toimistosta.
Elinkaaren taulukko näyttää muun muassa minkä tahansa ikäisen ja sukupuolen henkilön kuoleman todennäköisyyden vuonna 2014. Näiden tietojen avulla loin seuraavan taulukon, joka näyttää sekä kuoleman todennäköisyyden että odotetut pisteet kaikille ikäryhmille 0–100 ja molemmille sukupuolille.
Vuoden 2014 elinikäisten ja kuolleiden taulukko
| Ikä | Todennäköisyys Kuolema — Mies | Todennäköisyys Kuolema — Nainen | Odotettu Pisteet — Mies | Odotettu Pisteet — Naiset |
|---|---|---|---|---|
| 0 | 0,006320 | 0,005310 | 0,632000 | 0,531000 |
| 1 | 0,000403 | 0,000352 | 0,039852 | 0,034835 |
| 2 | 0,000282 | 0,000221 | 0,027626 | 0,021683 |
| 3 | 0.000211 | 0.000161 | 0,020514 | 0,015612 |
| 4 | 0.000181 | 0,000131 | 0,017405 | 0,012556 |
| 5 | 0.000161 | 0.000111 | 0,015313 | 0,010515 |
| 6 | 0,000141 | 0.000111 | 0,013260 | 0,010405 |
| 7 | 0,000131 | 0.000101 | 0,012184 | 0,009360 |
| 8 | 0.000121 | 0,000091 | 0.011127 | 0,008334 |
| 9 | 0,000091 | 0.000081 | 0,008256 | 0,007328 |
| 10 | 0.000101 | 0,000091 | 0,009073 | 0,008154 |
| 11 | 0.000101 | 0.000081 | 0,008973 | 0,007168 |
| 12 | 0,000131 | 0.000101 | 0,011535 | 0,008861 |
| 13 | 0,000202 | 0,000131 | 0,017547 | 0.011389 |
| 14 | 0,000303 | 0,000151 | 0,026023 | 0,012992 |
| 15 | 0.000404 | 0.000191 | 0,034304 | 0,016267 |
| 16 | 0.000505 | 0,000232 | 0,042393 | 0,019464 |
| 17 | 0,000616 | 0,000272 | 0,051129 | 0,022582 |
| 18 | 0,000748 | 0,000302 | 0,061316 | 0,024796 |
| 19 | 0.000880 | 0,000343 | 0,071262 | 0,027768 |
| 20 | 0,001022 | 0,000373 | 0,081780 | 0,029855 |
| 21 | 0.001145 | 0.000404 | 0,090445 | 0,031884 |
| 22 | 0.001258 | 0.000444 | 0,098105 | 0,034643 |
| 23 | 0.001310 | 0,000475 | 0.100880 | 0,036546 |
| 24 | 0,001332 | 0,000495 | 0.101246 | 0,037625 |
| 25 | 0,001344 | 0,000526 | 0.100811 | 0,039422 |
| 26 | 0,001377 | 0,000556 | 0.101864 | 0,041162 |
| 27 | 0,001389 | 0,000577 | 0.101371 | 0,042106 |
| 28 | 0,001421 | 0,000608 | 0.102330 | 0,043740 |
| 29 | 0.001454 | 0,000648 | 0.103234 | 0,046036 |
| 30 | 0,001507 | 0,000669 | 0.105517 | 0,046837 |
| 31 | 0.001530 | 0.000710 | 0.105584 | 0,048998 |
| 32 | 0,001574 | 0,000751 | 0.107011 | 0,051084 |
| 33 | 0,001617 | 0,000813 | 0.108364 | 0,054454 |
| 34 | 0,001661 | 0.000864 | 0.109644 | 0,057041 |
| 35 | 0.001716 | 0,000926 | 0.111521 | 0,060194 |
| 36 | 0,001781 | 0.001008 | 0.113970 | 0,064538 |
| 37 | 0,001857 | 0,001081 | 0.116963 | 0,068090 |
| 38 | 0,001933 | 0.001164 | 0.119830 | 0,072145 |
| 39 | 0.002020 | 0,001237 | 0.123207 | 0,075427 |
| 40 | 0.002118 | 0.001340 | 0.127066 | 0,080422 |
| 41 | 0,002258 | 0.001445 | 0,133232 | 0,085232 |
| 42 | 0.002410 | 0,001560 | 0,139778 | 0,090455 |
| 43 | 0,002615 | 0,001696 | 0,149075 | 0,096649 |
| 44 | 0,002843 | 0,001853 | 0,159228 | 0.103761 |
| 45 | 0,003105 | 0.002011 | 0,170771 | 0.110606 |
| 46 | 0,003401 | 0,002191 | 0,183635 | 0.118300 |
| 47 | 0,003742 | 0,002403 | 0.198314 | 0,127342 |
| 48 | 0,004108 | 0,002647 | 0,213613 | 0,137656 |
| 49 | 0,004532 | 0,002894 | 0.231133 | 0,147577 |
| 50 | 0,004994 | 0,003194 | 0,249696 | 0.159718 |
| 51 | 0,005473 | 0,003487 | 0,268191 | 0.170880 |
| 52 | 0,005993 | 0,003794 | 0,287656 | 0.182103 |
| 53 | 0,006565 | 0,004104 | 0.308561 | 0.192871 |
| 54 | 0,007159 | 0,004428 | 0,329324 | 0,203676 |
| 55 | 0,007799 | 0,004767 | 0,350946 | 0,214498 |
| 56 | 0,008475 | 0,005153 | 0,372902 | 0,226729 |
| 57 | 0,009179 | 0,005534 | 0,394696 | 0,237972 |
| 58 | 0,009856 | 0,005889 | 0,413944 | 0,247347 |
| 59 | 0,010575 | 0,006272 | 0,433558 | 0,257150 |
| 60 | 0.011350 | 0,006683 | 0,453991 | 0,267338 |
| 61 | 0.012209 | 0,007180 | 0,476135 | 0.280016 |
| 62 | 0,013061 | 0,007720 | 0.496330 | 0,293355 |
| 63 | 0,013921 | 0,008339 | 0,515084 | 0.308537 |
| 64 | 0,014814 | 0,009029 | 0,533320 | 0,325041 |
| 65 | 0,015831 | 0,009839 | 0,554094 | 0,344371 |
| 66 | 0,016981 | 0,010741 | 0,577354 | 0,365197 |
| 67 | 0,018300 | 0,011752 | 0.603909 | 0.387812 |
| 68 | 0,019778 | 0,012879 | 0,632894 | 0.412117 |
| 69 | 0,021443 | 0,014142 | 0,664734 | 0,438397 |
| 70 | 0,023384 | 0,015613 | 0.701513 | 0,468376 |
| 71 | 0,025547 | 0,017271 | 0,740873 | 0.500852 |
| 72 | 0,027877 | 0,019047 | 0,780560 | 0,533320 |
| 73 | 0,030384 | 0,020918 | 0.820374 | 0,564797 |
| 74 | 0,033098 | 0,022938 | 0,860535 | 0,596385 |
| 75 | 0,036256 | 0,025299 | 0,906400 | 0,632465 |
| 76 | 0,039868 | 0,028043 | 0,956841 | 0,673035 |
| 77 | 0,043883 | 0,031127 | 1.009299 | 0,715914 |
| 78 | 0,048257 | 0,034590 | 1.061657 | 0,760984 |
| 79 | 0,053128 | 0,038456 | 1.115692 | 0.807583 |
| 80 | 0,058709 | 0,043007 | 1.174177 | 0.860145 |
| 81 | 0,065070 | 0,048186 | 1.236322 | 0,915536 |
| 82 | 0,072149 | 0,053762 | 1.298691 | 0,967712 |
| 83 | 0,079906 | 0,059769 | 1.358409 | 1.016065 |
| 84 | 0.088524 | 0,066380 | 1.416378 | 1.062085 |
| 85 | 0,098157 | 0.073823 | 1.472348 | 1.107351 |
| 86 | 0.108904 | 0,082381 | 1.524651 | 1.153334 |
| 87 | 0.120889 | 0,092180 | 1.571556 | 1.198344 |
| 88 | 0.134134 | 0.103305 | 1.609607 | 1.239664 |
| 89 | 0.148707 | 0.115744 | 1.635778 | 1.273180 |
| 90 | 0,164522 | 0,129477 | 1.645220 | 1.294772 |
| 91 | 0.181584 | 0.144435 | 1.634254 | 1.299911 |
| 92 | 0.199903 | 0,160621 | 1.599225 | 1.284970 |
| 93 | 0,219362 | 0.177816 | 1.535534 | 1.244713 |
| 94 | 0,239881 | 0.196194 | 1.439286 | 1.177165 |
| 95 | 0,260293 | 0,214694 | 1.301463 | 1.073469 |
| 96 | 0.280129 | 0,233056 | 1.120515 | 0,932225 |
| 97 | 0,299042 | 0,251152 | 0.897125 | 0,753456 |
| 98 | 0,316317 | 0,268235 | 0,632634 | 0,536471 |
| 99 | 0,332667 | 0,284442 | 0,332667 | 0,284442 |
| 100 | 0.348651 | 0.301417 | 0.000000 | 0.000000 |
Taulukosta käy ilmi, että 90-vuotiaan miehen odotettu enimmäispistemäärä on 1,645220.
Tätä kysymystä on käsitelty ja siitä keskustellaan uhkapeleihin liittymättömällä Diversity Tomorrow -foorumillani.
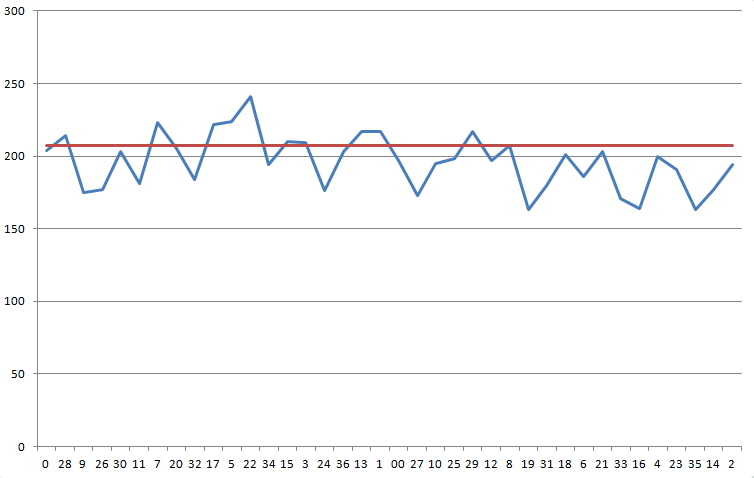
Tallensin 7 456 ruletin pyöräytystä. Tulokset ovat seuraavat. Epäilen, että rulettipyörä on puolueellinen, mutta en ole varma, onko data riittävän vakuuttavaa sen pelaamiseen.
Rulettitiedot
| Voittaminen Määrä | Esiintymiset |
|---|---|
| 0 | 204 |
| 28 | 214 |
| 9 | 175 |
| 26 | 177 |
| 30 | 203 |
| 11 | 181 |
| 7 | 223 |
| 20 | 205 |
| 32 | 184 |
| 17 | 222 |
| 5 | 224 |
| 22 | 241 |
| 34 | 194 |
| 15 | 210 |
| 3 | 209 |
| 24 | 176 |
| 36 | 203 |
| 13 | 217 |
| 1 | 217 |
| 00 | 197 |
| 27 | 173 |
| 10 | 195 |
| 25 | 198 |
| 29 | 217 |
| 12 | 197 |
| 8 | 207 |
| 19 | 163 |
| 31 | 180 |
| 18 | 201 |
| 6 | 186 |
| 21 | 203 |
| 33 | 171 |
| 16 | 164 |
| 4 | 200 |
| 23 | 191 |
| 35 | 163 |
| 14 | 177 |
| 2 | 194 |
| Kokonais | 7456 |
Seuraava kaavio näyttää tuloksesi peräkkäisessä järjestyksessä ruletissa. Sininen viiva näyttää tuloksesi. Punainen viiva on luku, jota tarvitset, 207,11, voittaaksesi 5,26 %:n talon edun.
Tämän jakauman khiin neliö -testi antaa tulokseksi 68,1 ja vapausasteita 37. Todennäköisyys sille, että tulos on näin vino tai enemmän, on 1:725.
En usko, että khiin neliö on täydellinen testi tähän tilanteeseen, koska se ei ota huomioon tulosten järjestystä, mutta en tiedä parempaakaan testiä. Jotkut ovat ehdottaneet Kolmogorov–Smirnovin testiä , mutta en usko, että se on sopiva. Jos on olemassa muita sopivia testejä, olen kuunnellut niitä mielelläni.
Voin sanoa, että jos olisit lyönyt vetoa kolmen numeron kaaresta numeron 5 ympärillä, olisit saanut 10,57 %:n voiton tallentamistasi pyöräytyksistä. Jos kuitenkin olisit kasvattanut sen seitsemän numeron kaareksi, etu putoaa 2,84 %:iin.
Jos minun olisi pakko vastata selkeällä englannilla, sanoisin, että rulettipyörä osoittaa todisteita, mutta ei kiistatonta näyttöä siitä, että pyörä on puolueellinen. Tämä puolueellisuus ei kuitenkaan luultavasti riitä merkittävästi ja varmasti voittamaan talon etua. Olettaen, että kasino ei vaihda rulettipyöriä pöytien välillä, sanoisin, että tietoa tulisi kerätä enemmän ennen suurten rahasummien panostamista. Olen pahoillani, että tämä vastaus on näin epämääräinen.
Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .
Kahdella pelaajalla, Samilla ja Danilla, on kummallakin viisi kolikkoa. Molempien on valittava yhdestä viiteen kolikkoa käteensä. Samalla molempien on paljastettava pelattujen kolikoiden määrä. Jos molemmat valitsevat saman määrän kolikoita, Sam voittaa ja kerää kaikki pelatut kolikot. Jos molemmat valitsevat eri määrän kolikoita, Dan kerää kaikki pelatut kolikot. Olettaen, että molemmat pelaajat ovat täydellisiä loogikoita, mikä on optimaalinen strategia Danille?
Danin tulisi satunnaistaa strategiansa seuraavasti:
- Yhden kolikon valitsemisen todennäköisyys = 77/548.
- Yhden kolikon valitsemisen todennäköisyys = 107/548.
- Yhden kolikon valitsemisen todennäköisyys = 117/548.
- Yhden kolikon valitsemisen todennäköisyys = 122/548.
- Yhden kolikon valitsemisen todennäköisyys = 125/548.
Tällä strategialla Dan voi odottaa voittavansa 3,640510949 kolikkoa joka vuorolla riippumatta siitä, kuinka monta kolikkoa Sami nostaa.
Ratkaisu löytyy matematiikkatehtävien sivustoltani, tehtävästä 230.
Tähän kysymykseen johtanut aiheeseen liittyvä kysymys löytyy foorumiltani Wizard of Vegasissa .
San Franciscon California Grand Casinolla pelataan blackjack-peliä nimeltä Hot Action Blackjack. Pelin säännöt ovat seuraavat:
- Kuusi pakkaa jatkuvassa sekoittajassa ja 18 jokeria, joiden nimellisarvo on 2.
- Jakaja lyö pehmeän 17.
- Tuplaa mitkä tahansa kaksi ensimmäistä korttia.
- Jaa uudelleen jopa neljään käteen.
- Ässien nostamista tai uudelleenjakamista ei sallita.
- Ei antautumista.
- Blackjack maksaa voittokertoimella 6–5.
- Jos pelaajan kaksi ensimmäistä korttia ovat jokereita, hän saa 4:1 bonuksen.
- Jos pelaajan kaksi ensimmäistä korttia ovat samaa maata olevia ässäkortteja, hän saa 5:1 bonuksen.
- Pelaajan on maksettava 5 %:n palkkio pelatakseen.
Mikä on perusstrategia ja talon etu?
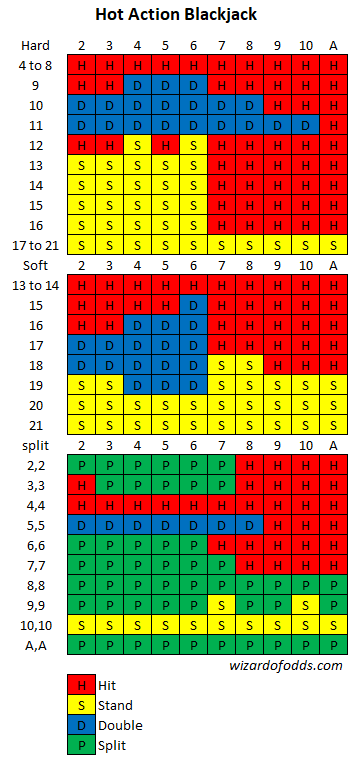
Ensinnäkin, tässä on perusstrategiani näiden sääntöjen mukaisesti:
Kaikki asiat huomioon ottaen talon eduksi arvioin 6,01 % (auts!) alkuperäiseen panokseen perustuen. Toisin sanoen, jos pelaaja panostaa 100 dollaria ilman 5 dollarin palkkiota, hän voi odottaa häviävänsä 6,01 dollaria. Tämä osoittaa, miksi pysyisin erossa pelaajan tallettamista peleistä Kaliforniassa, ellet ole itse se, joka asettaa itselleen talletuksen.
Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .