Kysy velholta #313
Mikä on Cleopatra Kenon varianssi?
Muistutuksena muille lukijoillemme, Cleopatra Kenoa pelataan kuten perinteistä kenoa, paitsi että jos viimeinen nostettu pallo vastaa yhtä pelaajan valinnoista JA johtaa voittoon, pelaaja voittaa myös 12 ilmaispeliä 2x kertoimella. Ilmaispelit eivät kerrytä lisää ilmaispelejä.
Et määrittänyt valintojen määrää tai voittotaulukkoa, joten käytetään esimerkkinä voittotaulukkoa 3-10-56-180-1000 pick-8. Lasketaan ensin tuotto.
Kenossa x pallon nappaamiskeinojen lukumäärä y:stä on sama kuin x pallon noppamiskeinojen lukumäärä 20:stä ja yx 60:stä. Tämä on yhtä kuin combin(20,x)*combin(60,yx) Excel-termein. Muistutuksena vielä, combin(x,y) = x!/(y!*(xy)!). Lopuksi x! = 1*2*3*...*x.
Nyt kun tuo katsaus on ohi, tässä on kyseisen voittotaulukon palautustaulukko. Oikea sarake näyttää voiton odotetun neliön, jota tarvitsemme myöhemmin.
Valitse 8 Kenoa
| Tapahtuma | Maksaa | Yhdistelmät | Todennäköisyys | Palata | Paluu^2 |
|---|---|---|---|---|---|
| 0 | 0 | 2 558 620 845 | 0,088266 | 0.000000 | 0.000000 |
| 1 | 0 | 7 724 138 400 | 0,266464 | 0.000000 | 0.000000 |
| 2 | 0 | 9 512 133 400 | 0.328146 | 0.000000 | 0.000000 |
| 3 | 0 | 6 226 123 680 | 0,214786 | 0.000000 | 0.000000 |
| 4 | 3 | 2 362 591 575 | 0,081504 | 0.244511 | 0,733533 |
| 5 | 10 | 530 546 880 | 0,018303 | 0.183026 | 1.830259 |
| 6 | 56 | 68 605 200 | 0,002367 | 0,132536 | 7.42.2014 |
| 7 | 180 | 4 651 200 | 0.000160 | 0,028882 | 5.198747 |
| 8 | 1000 | 125 970 | 0.000004 | 0,004346 | 4.345661 |
| Kokonais | 28 987 537 150 | 1.000000 | 0,593301 | 19.530214 |
Lasketaan seuraavaksi keskimääräinen bonus. Yllä olevasta taulukosta näemme, että keskimääräinen voitto bonusta lukuun ottamatta on 0,593301. Bonuksessa pelaaja saa 12 tuplattua ilmaiskierrosta. Näin ollen odotettu voitto bonuksesta on 2 × 12 × 0,593301 = 14,239212.
Lasketaan seuraavaksi bonusvoiton todennäköisyys. Jos pelaaja saa neljä numeroa, todennäköisyys sille, että 20. pallo on yksi näistä neljästä, on 4/20. Yleisesti ottaen, jos pelaaja saa c:n, todennäköisyys sille, että 20. pallo vaikutti voittoon, on c/20.
Bonuksen voittamiseksi käytetään kaavaa prob(catch 4)*(4/20) + prob(catch 5)*(5/20) + prob(catch 6)*(6/20) + prob(catch 7)*(7/20) + prob(catch 8)*(8/20). Tiedämme minkä tahansa voiton todennäköisyyden yllä olevasta palautustaulukosta. Bonuksen voittamisen todennäköisyys on siis:
0,081504 * (4/20) + 0,018303 * (5/20) + 0,002367 * (6/20) + 0,000160 * (7/20) + 0,000004 * (8/20) = 0,021644.
Bonuksen voittotodennäköisyyden ja keskimääräisen bonusvoiton avulla voimme laskea bonuksen tuoton muotoon 0,021644 × 14,239212 = 0,308198.
Ei meidän tarvitse tietää, mutta pelin kokonaistuotto on peruspelin tuotto plus bonuspelin tuotto, joka on 0,593301 + 0,308198 = 0,901498.
Aloitetaanpa nyt varsinaisen varianssin käsittely. Muistutuksena, yleinen varianssin kaava on:
var(x + y) = var(x) + var(y) + 2*cov(x,y), jossa var tarkoittaa varianssia ja cov tarkoittaa kovarianssia. Tässä pelin tapauksessa:
Kokonaisvarianssi = var(peruspeli) + var(bonus) + 2*cov(peruspeli ja bonus).
Varianssin peruskaava on E(x^2) - [E(x)]^2. Toisin sanoen odotetun voiton neliö vähennettynä odotetun voiton neliöllä.
Aloitetaan kuitenkin peruspelin varianssilla. Muistatko, kun sanoin aiemmin, että tarvitsemme ensimmäisen taulukon odotetun voiton neliön. Ensimmäisen taulukon oikeassa alakulmassa oleva solu näyttää meille odotetun voiton neliön, joka on 19,530214. Tiedämme jo, että odotettu voitto on 0,593301. Näin ollen peruspelin varianssi on 19,530214 - 0,593301 2 = 19,178208.
Lasketaan seuraavaksi bonuksen varianssi (olettaen, että se on jo osunut). Muistakaa tätä varten, että:
var(ax) = a 2 x, missä a on vakio.
Muista myös, että n satunnaismuuttujan x varianssi on nx.
Jos x on bonuspelin perusvoitto, koko bonuspelin varianssi on 2 2 × 12 × x. Tiedämme yllä olevasta, että yhden pyöräytyksen varianssi peruspelissä, bonuspeliä lukuun ottamatta, on 19,178208. Joten bonuksen varianssi, olettaen, että bonus on jo osunut, on 2 2 × 12 × 19,178208 = 920,554000.
Meidän on kuitenkin tiedettävä bonuksen varianssi ennen ensimmäisen pallon arvontaa, mukaan lukien mahdollisuus, että bonusta ei voiteta ollenkaan. Emme voi vain kertoa bonuksen varianssia sen voittotodennäköisyydellä. Sen sijaan muistakaamme, että var(x) = E(x^2) - [E(x)]^2. Järjestetään se uudelleen muotoon:
E(x^2) = muutt(x) + [E(x)]^2
Tunnemme bonuksen keskiarvon ja varianssin, joten bonuksen odotettu voitto neliöitynä on 920,554000 + 19,178208 2 = 1123,309169.
Joten bonusvoiton odotettu neliö ennen ensimmäisen pallon nostamista on tod(bonus) × E(x^2) = 0,021644 × 1123,309169 = 24,313239.
Laskimme jo, että bonuksen odotettu voitto ennen ensimmäistä palloa on 0,308198. Joten bonuksen kokonaisvarianssi ennen ensimmäistä palloa on 24,313239 - 0,308198 2 = 24,218253.
Seuraava vaihe on kovarianssin laskeminen. Saatat kysyä, että "Miksi perusvoiton ja bonusvoiton välillä on korrelaatio?". Se johtuu siitä, että viimeisen nostetun pallon on myötävaikutettava voittoon, jotta bonus aktivoituu. Koska viimeinen pallo myötävaikutti voittoon, keskimääräinen voitto kasvaa. Muistutuksena Bayesin ehdon todennäköisyyden kaava sanoo:
P(A annettuna B) = P(A ja B)/P(B).
Tehdään sitten peruspelin palautustaulukko uudelleen, koska viimeinen pallo oli osuma:
Valitse 8 Kenoa, kun viimeinen pallo osui
| Tapahtuma | Maksaa | Yhdistelmät | Todennäköisyys | Palata |
|---|---|---|---|---|
| 0 | 0 | - | 0.000000 | 0.000000 |
| 1 | 0 | - | 0.000000 | 0.000000 |
| 2 | 0 | - | 0.000000 | 0.000000 |
| 3 | 0 | - | 0.000000 | 0.000000 |
| 4 | 3 | 472 518 315 | 0,753119 | 2.259358 |
| 5 | 10 | 132 636 720 | 0.211402 | 2.114019 |
| 6 | 56 | 20 581 560 | 0,032804 | 1.837010 |
| 7 | 180 | 1 627 920 | 0,002595 | 0,467036 |
| 8 | 1000 | 50 388 | 0.000080 | 0.080310 |
| Kokonais | 627 414 903 | 1.000000 | 6.757734 |
Oikeassa alakulmassa oleva solu näyttää, että olettaen, että viimeinen pallo oli osuma, keskimääräinen voitto on 6,757734.
Seuraavaksi, muista yliopiston tilastotieteen kurssilta, että:
cov(x,y) = exp(xy) - exp(x)*exp(y) .
Olkoon x meidän tapauksessamme peruspelin voitto ja y bonusvoitto. Työskennellään ensin exp(xy):n kanssa.
Exp(xy) = tod(bonusvoitto)*(keskimääräinen peruspelin voitto annettu bonus voitettu)*keskiarvo(bonusvoitto) + tod(bonusta ei voitettu)*(keskimääräinen peruspelin voitto annettu bonus ei voitettu)*keskiarvo(bonusvoitto annettu bonus ei voitettu). On helppo sanoa, että keskiarvo(bonusvoitto annettu bonus ei voitettu) = 0, joten voimme kirjoittaa uudelleen seuraavasti:
Exp(xy) = tod(bonusvoitto)*(keskimääräinen peruspelin voitto bonuksen perusteella)*keskiarvo(bonusvoitto) =
0,021644 × 6,757734 × 14,239212 = 2,082719.Olemme jo ratkaisseet E(x):n ja E(y):n, joten kovarianssi on:
cov(x,y) = exp(xy) - exp(x)*exp(y) = 2,082719 - 0,593301 × 0,308198 = 1,899865.
Palataanpa varianssin kokonaisyhtälöön, kun kovarianssi on mukana:
Kokonaisvarianssi = var(peruspeli) + var(bonus) + 2*cov(peruspeli ja bonus) = 19,178208 + 24,218253 + 2×1,899865 = 47,196191. Keskihajonta on sen neliöjuuri, joka on 6,869948.
Siinäpä se. Minulla meni siihen tuntikausia, joten toivottavasti olet tyytyväinen.
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Olen kuullut, että avioliiton päättymisen todennäköisyys, jonka Yhdysvalloissa yleensä sanotaan olevan 50 %, lasketaan suhteuttamalla avioerojen lukumäärä saman ajanjakson aikana solmittujen avioliittojen lukumäärään. Onko se totta? Pidätkö sitä oikeudenmukaisena tapana laskea tilastoa? Kyseenalaistan sen, koska vertaat avioeroja lyhyen ajan kuluessa solmittuihin avioliittoihin pitkän ajan kuluessa.
Jos väestö ja ikäjakauma pysyisivät vakaina ja avioeron todennäköisyys olisi todella 50 %, odottaisimme suuren otoskoon perusteella näkevämme yhden avioeron ja kahden avioliiton suhteen millä tahansa ajanjaksolla.
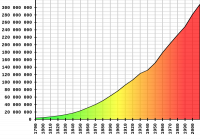
Väestö ei kuitenkaan ole vakaa. Tästä kaaviosta näyttää siltä, että Yhdysvaltojen väestö kasvaa 10,71 % vuosikymmenessä. Se tekee 1,02 % vuodessa. Sanotaanpa vain 1 % yksinkertaisuuden vuoksi.
Karttalähde: Yhdysvaltain väestönlaskenta
Fatherly.comin mukaan epäonnistuneen avioliiton keskimääräinen pituus on 8 vuotta.
Jos tarkkailisit avioerojen ja avioliittojen suhdetta nykyhetkellä 1:2, mikä olisi keskimääräinen todennäköisyys sille, että jokin tietty avioliitto päättyy avioeroon?
Nykyiset avioerot solmittiin kahdeksan vuotta sitten, jolloin väestö oli 92,35 % nykyisestä. Yksinkertainen matematiikka viittaa siihen, että avioeron todellinen todennäköisyys on 54,14 %.
Tarkistetaanpa se.
Ensinnäkin CDC:n mukaan vuosittain solmitaan 6,9 avioliittoa 1 000 asukasta kohden. Tämä luku ei ole relevantti käsillä olevan kysymyksen kannalta, mutta mielestäni se auttaa ymmärtämään asiaan liittyviä lukuja.
Oletetaan, että väkiluku oli 8 vuotta sitten 300 000 000. Se olisi 0,69 % * 300 miljoonaa = 2 070 000 avioliittoa sinä vuonna.
Jos 54,14 % heistä päättyy avioeroon kahdeksan vuotta myöhemmin, niin näkisimme 2 070 000 * 54,14 % = 1 120 698 avioeroa nykyhetkellä.
1 120 698 / 2 070 000 = 50 % havaittu avioerojen ja avioliittojen suhde nykyhetkellä.
Jotta kukaan ei sitä sanoisi, tiedän kyllä, etteivät kaikki avioerot pääty tasan kahdeksaan vuoteen. Kaiken kaikkiaan kuitenkin sanon, että lopputulos ei ole kaukana todellisesta 54,14 prosentin avioeroprosentistani.
Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .
Toimistossasi sadan työntekijän ryhmässä järjestetään salainen joulupukin lahjavaihto. Siinä kirjoitetaan kaikkien nimet yksittäisille paperilapuille, laitetaan ne hattuun ja jokainen arpoo satunnaisesti nimen, jolle hän antaa lahjan.
Kysymys kuuluu, kuinka monta suljettua silmukkaa keskimäärin on? Esimerkiksi suljetussa silmukassa Gordon antaa Donille, joka antaa Jonille, joka antaa Nathanille ja joka antaa Gordonille. Tai oman nimesi arpominen.
Harkitse, että jokainen valitsee yhden kerrallaan. Kun jokainen valitsee, on kahdenlaisia tilanteita:
- Valittavan nimi on jo valittu.
- Valitun nimi on edelleen nimilaatikossa.
Oletetaan, että mille tahansa poimijalle on jäljellä n henkilöä poimittavana.
Jos valitsevan henkilön nimi on jo valittu, on 1/n todennäköisyys, että valitseja valitsee oman nimensä sisältävän silmukan. Oletetaan esimerkiksi, että Amy valitsee. Amyn nimi on jo Bobin hallussa, Bobin nimi on jo Charlien hallussa ja Charlien nimi on edelleen laatikossa. Kun laatikossa on vielä n nimeä, on 1/n todennäköisyys, että Amy valitsee Charlien nimen, mikä sulkee silmukan.
Jos valitsevan henkilön nimeä ei ole vielä valittu, on 1/n mahdollisuus, että Amy valitsee oman nimensä, jolloin silmukka sulkeutuu.
Joka tapauksessa, jos poimija ei sulje silmukkaa, hän liittyy osaan toista ketjua, jonka joku muu lopulta sulkee. Jokainen ketju lasketaan vain kerran, kun se sulkeutuu.
Näin ollen vastaus on 1/100 + 1/99 + 1/98 + ... + 1/1 =~ 5,187377518.
Riittävän suurelle pelaajien määrälle n saadaan arvio ln(n).
Kysymys on esitetty ja siitä keskustellaan foorumillani Wizard of Vegasissa .
Kuinka paljon ylimääräinen taattu wild-symboli olisi videopeliautomaatin pelaamisen arvoinen?
Se riippuu monista asioista. Tulkitsen kysymyksesi sillä, mikä on ylimääräisen wild-symbolin arvo pelaajan normaalin keskimääräisen määrän lisäksi. Vaikka vastaus vaihtelee merkittävästi pelistä toiseen, merkittävä tekijä on rivien lukumäärä ruudulla. Jos rivejä on kolme, ylimääräinen wild-symboli vaikuttaa 1/3 voittolinjoista. Vastaavasti, jos rivejä on neljä, se on vähemmän arvokas ja vaikuttaa 1/4 voittolinjoista.
Vastatakseni kysymykseesi, tarkastelin peliä Cleopatra , jonka olen jo dekonstruoinut. Seuraava taulukko näyttää wild-symbolin odotusarvon kasvun verrattuna satunnaiseen määrään wildeja.
Extra Wildin arvo Cleopatrassa
| Kela | 3 riviä | 4 riviä |
|---|---|---|
| 1 | 95,71 % | 71,79 % |
| 2 | 99,76 % | 74,82 % |
| 3 | 76,24 % | 57,18 % |
| 4 | 21,25 % | 15,93 % |
| 5 | 1,96 % | 1,47 % |