Kysy velholta #321
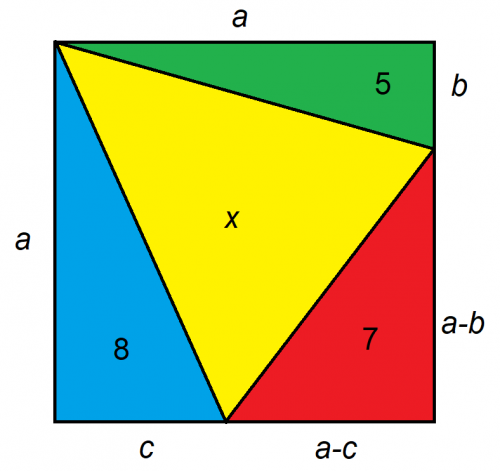
Oletetaan, että suurempi kuvio on neliö, niin mikä on x:n pinta-ala?
Tällaisten ongelmien avain on niiden asettelussa. Suosittelen yrittämään tiivistää ongelman mahdollisimman vähään tuntemattomaan. Tässä tapauksessa voimme ilmaista tuntemattomat etäisyydet neliöllä vain kolmeksi seuraavasti:
Suorakulmioiden käsittely on helpompaa kuin kolmioiden. Koska tiedämme kolmen kolmion pinta-alan, voimme kaksinkertaistaa koon ja pinta-alan. Se antaa meille:
- noin = 10
- ac=16
- (ab)(ac)=14
Jaetaan tekijöihin (ab)(ac):
a 2 - ab - ac + bc = 14
a 2 - 10 - 16 + bc = 14
(1) a² + bc = 40
Ilmaistaan b ja c muuttujan a avulla, jotta saadaan tämä yhteen muuttujaan:
b = 10/a
c = 16/a
Sijoittamalla b ja c näillä arvoilla yhtälöön (1):
2 + (10/a)*(16/a) = 40
a² + 160 / a² = 18
Seuraavaksi poistetaan nimittäjässä oleva 2 kertomalla kaikki luvulla 2 .
4 + 160 = 40 * 2
4–40 * 2 + 160 = 0
Määritellään uusi muuttuja y = a 2
v 2 - 18 v + 32 = 0
Ratkaistaan seuraavaksi y käyttämällä toisen asteen kaavaa:
y = (40 +/- neliöjuuri(1600-640))/2
y = (40 +/- neliöjuuri(960))/2
y = (40 +/- 8 * neliöjuuri(15))/2
y = 20 +/- 4*neliömetriä(15)
Koko neliön pinta-ala on a2 , joka on kätevästi yhtä suuri kuin y. Yllä olevan yhtälön mukaan, jos +/- on negatiivinen, niin y = apx 4,5081, mikä on ilmeisen väärin, koska tiedämme pinta-alan olevan vähintään 20, edes x:ää lukuun ottamatta. Joten neliön pinta-alan on oltava 20 + 4*sqrt(15).
Kolmen annetun kolmion pinta-ala on 5 + 7 + 8 = 20. Vähentämällä tämä neliön kokonaispinta-alasta saadaan x:n pinta-ala: 20 + 4 * sqrt(15) - 20 = 4 * sqrt(15) = appx 15,4919.
Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .

Huomaa t-paitani tässä kuvassa. Elokuvateatterin kassa kehui sitä, kun menin katsomaan elokuvaa Uncut Gems . Kiitin häntä kiduttamalla häntä tällä tehtävällä, mutta käyttäen vain kolmioita, joiden pinta-alat ovat 2, 3 ja 4. Elokuvan jälkeen tarkistin hänen vointinsa, eikä hän ollut vieläkään ratkaissut tehtävää, mutta näytti yrittävän. Niinpä kirjoitin hänelle seuraavan ratkaisun Suncoast-baarissa. Hän itse asiassa näytti arvostavan sitä. Uskon, että tuo nuori nainen pääsee pitkälle elämässä.
Onko usean osavaltion lottopelien (Powerball, Mega Millions) päävoiton koon suhteen olemassa "käännekohta", jossa on todennäköisempää, että pääpalkinto jaetaan, kuin että voittaja on yksi? Jos on, mikä tämä summa on?
En aio mennä kaikkeen matematiikkaan, mutta tässä ovat jättipottipisteet, joissa usean voittajan todennäköisyys on yhtä suuri kuin täsmälleen yhden:
- PowerBall: 975 miljoonaa dollaria
- Mega Millions: 1,65 miljardia dollaria
Ei niin, että kysyit, mutta tässä ovat jättipotit, joissa ainakin yhden voittajan todennäköisyys on yhtä suuri kuin yhdenkään voittajan todennäköisyys (50 %).
- PowerBall: 704 miljoonaa dollaria
- Mega Millions: 867 miljoonaa dollaria
Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .
- Vankilassa on 12 vankia, jotka on numeroitu 1-12.
- Vankilanjohtaja asettaa 12 laatikkoa, joista jokainen on numeroitu 1–12.
- Kahdentoista laatikon sisällä on satunnaisesti sijoitellut numerot 1–12, yksi jokaiseen laatikkoon.
- Jokainen vanki saa avata kuusi valitsemaansa laatikkoa yksi kerrallaan. Hän voi valita ja avata ne yksi kerrallaan.
- Jokaisen vangin tavoitteena on löytää oma numeronsa laatikon sisältä kuuden vaihtoehdon joukosta. Jos hän onnistuu, henkilön sanotaan selviävän.
- Jos vanki ei löydä omaa numeroaan, koko ryhmän sanotaan epäonnistuneen ja heidät viedään välittömästi teloitusryhmän luo.
- Jos vanki selviää hengissä, hänen on laitettava numerot takaisin alkuperäisiin laatikoihinsa seuraavaa vankia varten.
- Vangit eivät saa katsoa muita pelaajia tai kommunikoida pelin alettua.
- Ennen aloittamista koko ryhmä saa tehdä yhteistyötä strategian laatimiseksi. Tavoitteena on, että kaikki 12 vankia selviävät hengissä (eli löytävät oman numeronsa laatikon sisältä).
Millainen strategia heidän tulisi olla selviytymistodennäköisyytensä maksimoimiseksi, ja mikä tuo todennäköisyys on?
Aivan kuten Secret Santa -pelissä, pelissä on silmukoita, jotka johtavat numerosta toiseen. Kahdentoista vangin tapauksessa silmukoita voi olla 1–12. Jos mikään silmukka ei ole pidempi kuin kuusi, jokainen vanki löytää lopulta oman numeronsa. Suuri kysymys on, mikä on todennäköisyys, ettei mikään silmukka ole suurempi kuin kuusi? Käännetäänpä se päinvastaiseksi ja etsitään niiden yhdistelmien lukumäärä, joiden silmukan koko on 7 tai enemmän.
12 Vankiratkaisu
| Silmukat | Yhdistelmät | Todennäköisyys |
|---|---|---|
| 12 | 39 916 800 | 0,083333 |
| 11,1 | 43 545 600 | 0,090909 |
| 10,2 | 23 950 080 | 0,050000 |
| 10,1,1 | 23 950 080 | 0,050000 |
| 9,3 | 17 740 800 | 0,037037 |
| 9,2,1 | 26 611 200 | 0,055556 |
| 9,1,1,1 | 8 870 400 | 0,018519 |
| 8,4 | 14 968 800 | 0,031250 |
| 8,3,1 | 19 958 400 | 0,041667 |
| 8,2,2 | 7 484 400 | 0,015625 |
| 8,2,1,1 | 14 968 800 | 0,031250 |
| 8,1,1,1,1,1 | 2 494 800 | 0,005208 |
| 7,5 | 13 685 760 | 0,028571 |
| 7,4,1 | 17 107 200 | 0,035714 |
| 7,3,2 | 11 404 800 | 0,023810 |
| 7,3,1,1 | 11 404 800 | 0,023810 |
| 7,2,2,1 | 8 553 600 | 0,017857 |
| 7,2,1,1,1 | 5 702 400 | 0.011905 |
| 7,1,1,1,1,1,1 | 570 240 | 0.001190 |
| Kokonais | 312 888 960 | 0,653211 |
Seuraavassa taulukossa on esitetty yllä olevan taulukon yhdistelmien kaavat.
Yhdistelmäkaavat
| Silmukat | Yhdistelmät | Kaava |
|---|---|---|
| 12 | 39916800 | =FAKTA(11) |
| 11,1 | 43545600 | =KOMBIN(12;11)*FAKTA(10) |
| 10,2 | 23950080 | =KOMBIN(12;10)*FAKTA(9) |
| 10,1,1 | 23950080 | =KOMBIN(12;10)*FAKTA(9) |
| 9,3 | 17740800 | =KOMBIN(12;9)*FAKTA(8)*FAKTA(2) |
| 9,2,1 | 26611200 | =YHDISTÄ(12,9)*YHDISTÄ(3,2)*FACT(8) |
| 9,1,1,1 | 8870400 | =KOMBIN(12;9)*FAKTA(8) |
| 8,4 | 14968800 | =KOMBIN(12;8)*KERTOMUS(7)*KERTOMUS(3) |
| 8,3,1 | 19958400 | =YHDISTÄ(12,8)*YHDISTÄ(4,3)*FACT(7)*FACT(2) |
| 8,2,2 | 7484400 | =YHDISTÄ(12,8)*YHDISTÄ(4,2)*FACT(7)/2 |
| 8,2,1,1 | 14968800 | =YHDISTÄ(12,8)*YHDISTÄ(4,2)*FACT(7) |
| 8,1,1,1,1,1 | 2494800 | =KOMBIN(12;8)*FAKTA(7) |
| 7,5 | 13685760 | =KOMBIN(12;7)*KERTOMUS(6)*KERTOMUS(4) |
| 7,4,1 | 17107200 | =KOMBIN(12;7)*5*FAKTA(6)*FAKTA(3) |
| 7,3,2 | 11404800 | =YHDISTÄ(12,7)*YHDISTÄ(5,3)*FACT(6)*FACT(2) |
| 7,3,1,1 | 11404800 | =YHDISTÄ(12,7)*YHDISTÄ(5,3)*FACT(6)*FACT(2) |
| 7,2,2,1 | 8553600 | =COMBIN(12,7)*COMBIN(5,2)*COMBIN(3,2)*FACT(6)/2 |
| 7,2,1,1,1 | 5702400 | =YHDISTÄ(12,7)*YHDISTÄ(5,2)*FACT(6) |
| 7,1,1,1,1,1,1 | 570240 | =KOMBIN(12;7)*FAKTA(6) |
Ensimmäisen taulukon oikeasta alakulmasta löytyy 312 888 960 häviävää yhdistelmää. Numerot voidaan järjestää yhteensä 12 eri tavalla! = 479 001 600. Näin ollen epäonnistumisen todennäköisyys on 312 888 960 / 479 001 600 = 65,32 %. Onnistumisen todennäköisyys on siis 100 % - 65,32 % = 34,68 %.
Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .
Hei. Minulla on kuponki, jolla voin puskea käteni 22:een. Voin pitää kupongin voimassa ensimmäiseen 22:een asti. Se ei koske tuplauksia tai jakoja. Mikä on tämän arvo?
Nopea vastaus on maksimipanos, jonka saat asettaa. Odota vain, kunnes saat 22, ja pelaa se sitten, jolloin saat yhden ylimääräisen yksikön.
Tarkemman vastauksen pitäisi tarkastella tuon 22:n odottamisen kustannuksia. Tätä en tiedä tarkalleen, mutta voin arvioida.
Jakaja-työntää-22-säännön hinta pelaajalle on 6,91 %. Jakaja pääsee kuitenkin 22:een enemmän, koska pelaajaa ei kiinnosta, vaikka olisi mennyt yli pelin ensin. Säännöistä riippuen pelaaja menee yli pelin noin 15,7 % ajasta. Jos oletamme, että tämä ei ole korreloitunut jakajan menetyksen todennäköisyyden kanssa (mitä se ei ole), niin jakajan menetyksen todennäköisyys on 6,91 % / (1,0 - 0,157) = 8,2 %.
Tiedän, että tämä on karkeaa, mutta oletetaan, että pelaajan 22:n todennäköisyys on sama. Tiedän, että jakaja häviää useammin kuin pelaaja, mutta tämä kuponki ei myöskään lasketa jaon jälkeen, joten sanotaan vain, että nämä tekijät kumoavat toisensa. Joten jos pelaaja saa 22:n 8,2 %:ssa käsistä, hän saa 22:n keskimäärin kerran 1/0,082 = 12,2 käden välein.
Oletetaan, että talon etu peruspelissä on 0,75 %. 12,2 käden pelaamisen hinta tällä talon edulla on 12,2 * 0,0075 = 0,0915. Vähennä tämä siis yhden yksikön arvosta, niin saat kupongin arvon 1,0 - 0,0915, joka on noin 91 % nimellisarvosta.
Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .