Kysy velholta #322
Istuin alas pelaamaan Texas Hold 'Emiä ja käynnissä olevan käden korkein käsi oli värisuora. Kaksi muuta pöydässä ollutta pelaajaa huomautti, että se oli kolmas peräkkäinen värisuora. Mitkä ovat tämän todennäköisyydet?
Kymmenen pelaajan Texas Hold 'Em -pelissä, olettaen, että kukaan ei koskaan luovuta, todennäköisyys sille, että korkea käsi on suora tai kuningasvärisuora, on 1/350,14. Todennäköisyys sille, että tämä tapahtuu kolmessa kädessä kolmesta, on 1/42 926 491.
Tuo pöytä on kuitenkin saattanut olla toiminnassa tuntikausia. Ehkä realistisempi kysymys on, mikä on todennäköisyys, että näin tapahtuisi ainakin kerran kokonaisen päivän aikana. Olettaen, että peliä on täydet 24 tuntia ja 24 kättä tunnissa, vastaus tähän kysymykseen olisi 1/59 621.
Tätä kysymystä on kysytty ja siitä keskustellaan foorumillani Wizard of Vegasissa .
Olettaen oikean strategian, mikä on voittotodennäköisyys, kun panos korotetaan nelinkertaisesti Ultimate Texas Hold 'Emissa? Kirjasin 96 nelinkertaista kättä. Laskematta puskeja, minulla oli 66 voittoa ja 30 tappiota. Miten tämä vertautuu odotuksiin?
Olettaen oikean 4x korotusstrategian, kunkin lopputuloksen todennäköisyys on olemassa 4x korotuksen yhteydessä:
- Voitto: 58,82 %
- Häviö: 38,47 %
- Tasapeli: 2,72 %
Jos tasapelit jätetään huomiotta, voittotodennäköisyys on 60,46 %. 96 ratkaistulla kädellä nelinkertaisten voittojen odotusarvo on 58,04. Joten 66 voittoa on odotettua suurempi, mutta ei merkittävästi.
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Axelilla ja Bobilla on kummallakin omat 52 kortin pakkansa. Molemmat sekoittavat ne satunnaisesti. Sitten he kääntävät yhden kortin kerrallaan, samanaikaisesti, kummastakin pakasta. Mikä on todennäköisyys, että he kääntävät saman kortin samaan aikaan ainakin kerran?
Vastaus olisi helppo arvioida muotoon 1-(51/52) 52 = 0,63568648. Arviot ovat kuitenkin älyllisesti niin epätyydyttäviä. Joten etsitään tarkka ratkaisu!
Vaihe 1: Aloita miettimällä, kuinka monella tavalla toinen pakka voidaan järjestää, kun ensimmäinen kortti on numero 1. Vastaus on kuinka monella tavalla muut 51 korttia voidaan järjestää, eli 51! = 1551118753287382280224243016469303211063259720016986112000000000000.
Mikä tahansa kortti voi sopia ensimmäiseen pakkaan, joten meidän on tehtävä tämä kaikille 52 kortille. Tämä antaa meille 52 * 51! = 52! yhdistelmää, joissa ainakin yksi kortti sopii.
Vaihe 2: Vaiheessa 1 kuitenkin lasketaan kaksinkertaisesti jokainen tilanne, jossa kaksi korttia on samanarvoisia. Esimerkiksi, jos kaksi ensimmäistä korttia olisivat 1 ja 2, olisimme laskeneet 50! tapaa järjestää muut kortit kahdesti, kerran siten, että 1 olisi ensimmäinen kortti ja toisen kerran siten, että 2 olisi toinen kortti. Tapojen lukumäärä 2 kortille 52:sta on combin(52,2) = 1326. Jokaista kahden kortin yhdistelmää kohden on 50! = 3041409320171337804361260816606476884437764156896051200000000000000 tapaa järjestää muut kortit. Näin ollen vaiheessa 2 meidän on vähennettävä combin(52,2)*50! = (52*51/2!)*50! = 52!/2! yhdistelmät.
Vaihe 3: Tarkastellaan seuraavaksi tilannetta, jossa satunnaispakan kolme ensimmäistä korttia ovat järjestyksessä 1, 2 ja 3. Loput 49 korttia voidaan järjestää 49! eri tavalla. Ensimmäisessä vaiheessa olisimme laskeneet ne kolme kertaa, jotta löytäisimme ainakin yhden samanlaisen kortin. Sitten toisessa vaiheessa olisimme vähentäneet kaikki combin(3,2)=3 tapaa valita kaksi näistä kolmesta kortista. Joten tämä tilanne olisi laskettu 3 - 3 = 0 kertaa, joten meidän on lisättävä ne takaisin. On olemassa combin(52,3) tällaista tilannetta, joissa valitaan ainakin kolme samaa korttia. Joten meidän on lisättävä takaisin combin(52,3)*49! = 52*51*50*49!/3! = 52!/3! yhdistelmät.
Vaihe 4: Tarkastellaan seuraavaksi tilannetta, jossa satunnaispakan neljä ensimmäistä korttia ovat järjestyksessä 1, 2, 3 ja 4. Loput 48 korttia voidaan järjestää 48! eri tavalla. Olisimme laskeneet ne neljä kertaa ensimmäisessä vaiheessa, jossa laskettiin ainakin yksi sama kortti. Sitten olisimme vähentäneet kaikki combin(4,2)=6 tapaa valita kaksi näistä neljästä kortista vaiheessa 2. Sitten olisimme laskeneet yhteen kaikki combin(4,3)=4 tapaa valita 3 näistä neljästä kortista. Joten olemme 4-6+4=2 tavalla, joilla jokainen tällainen tilanne olisi laskettu. Joten meidän on vähennettävä yksi näistä tavoista, jotta jokainen tilanne lasketaan kerran. On combin(52,4)*48! = 52*51*50*49*48!/4! = 52!/4! tällaisia tilanteita, jotka on lisättävä takaisin.
Jatkamme tätä vuorotellen yhteen- ja vähennyslaskuja korjataksemme kaksinkertaisen laskennan.
Loppujen lopuksi tilanteiden lukumäärä, joissa ainakin yksi satunnaispakan kortti vastaa järjestettyä pakkaa = combin(52,1)*51! - combin(52,2)*50! + combin(52,3)*49! - combin(52,4)*48! ... - combin(52,52)*1! = 52!/1! - 52!/2! + 52!/3! - 52!/4! ... - 52!/52! = x = 333239808909468890675694068318655265019682314241643033726180828783.
Kortteja voi tilata yhteensä 52! = y = 52717761549636521942261854154512265996921245386198220800000000000000 Yhteensä 52 kortin tilaustapoja.
Näin ollen vastaus on x/y = 0,6321205588285576784044762298
Todennäköisyys sille, ettei osumia löydy, on 1-(x/y) = 0,3678794411714423215955237702.
Jos tämä luku näyttää tutulta, sen pitäisikin näyttää tutulta. 1/e = 0,3678794411714423215955237702.
Joten vastaus voidaan arvioida HYVIN tarkasti muotoon 1-(1/e).
Kiitokset
Matemaattiset laskelmat tehtiin Pari/GP: ssä
Tätä ongelmaa kysyttiin ja siitä keskusteltiin foorumillani Wizard of Vegasissa .
Sivustollasi olevassa bingokuvioiden todennäköisyyksiä käsittelevässä PDF-tiedostossa ilmoitat, että voittajan löytämiseen tarvittavien puheluiden odotettu määrä olettaen, että pelissä on 300 korttia, on seuraava:
- Neljä kulmaa: 8.43
- Pieni timantti: 11.833
Molemmat kuviot vaativat vain neljä pistettä ja niillä on vain yksi tapa voittaa. Miksi voittajan löytämiseen tarvittavien pallojen odotettu määrä on erilainen?
Tähän on vaikea vastata. Aloitan sanomalla, että yhden kortin pelissä odotettu puheluiden määrä olisi sama. Useamman kuin yhden kortin pelissä on kuitenkin korrelaatiovaikutus.
Tähän on vaikea antaa nopeaa vastausta, mutta jos se on pakotettu, se johtuu siitä, että neljän kulman kuvio vaatii pallojen keskittymisen B- ja O-sarakkeisiin. Pieni vinoneliön muotoinen kuvio osuu todennäköisemmin, jos pallot jakautuvat tasaisesti B-, N- ja O-sarakkeisiin.
Yksinkertaistetaan peli sellaiseksi, jossa pelissä on ääretön määrä kortteja ja pallot nostetaan korvaavalla kortilla. Tässä on pallojen lukumäärä, joka tarvitaan voittajan löytämiseen molemmissa peleissä:
- Neljä kulmaa: 2,5 + 2,5 + ((1/2) * 10 + (1/2) * (2,5 + 5)) = 13,75
- Pieni timantti: =(5/3)+((1/3)*((5/3)+(5/2)+5)+(2/3)*((5/2)+((1/2)*((5/2)+5)+(1/2)*(5+5)))) = 12 + 2/9
Tämä osoittaa, että neljä kulmaa vie 1,53 palloa enemmän.
Suorittamalla tämän simulaation normaaleilla bingosäännöillä ja olettaen äärettömän määrän kortteja, tulokset ovat seuraavat:
- Neljä kulmaa: 12.8289
- Timantti: 11.3645
Tällä kertaa erilainen, 1,46 palloa.
Toivon osoittaneeni, että kuviot peittyvät todennäköisemmin nopeammin, jos pisteet jakautuvat useampaan sarakkeeseen. Tästä syystä mielestäni yhden bingon pelissä voittava bingo on yleensä vaakasuorassa.
Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .
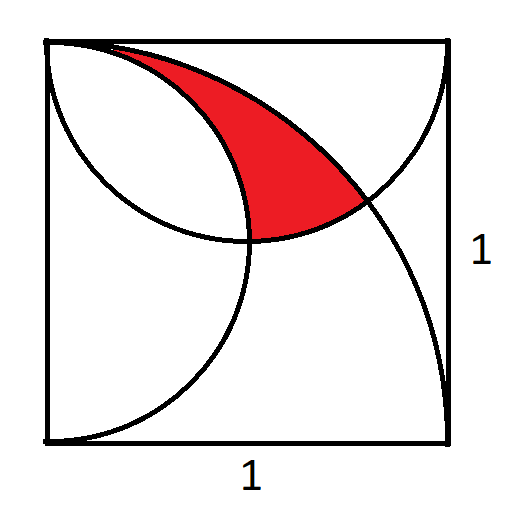
Yllä olevassa kuvassa on neljännesympyrä ja kaksi puoliympyrää neliössä, jonka sivun pituus on yksi. Kysymys kuuluu, mikä on punaisen alueen pinta-ala?
Klikkaa seuraavaa painiketta nähdäksesi vastaukseni.
Napsauta seuraavaa painiketta nähdäksesi ratkaisuni.
Tässä on linkki ratkaisuuni . (PDF)
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Kiitokset: Haluan kiittää Mind Your Decisionsia tästä matemaattisesta pulmasta.


