Kysy velholta #323
Onko tämä parlay-kortti hyvä?

Ensimmäisessä vaiheessa sinun on lyötävä vetoa NFL-ottelun tasoitusta vastaan kummallakin tavalla. Kun kysyit tätä kysymystä (2. tammikuuta 2020), Vikings oli 7,5 pisteen altavastaaja. NFL:n vaihtoehtoisen pistetasoituksen laskurini mukaan Vikingsin +8,5-voiton todennäköisyys kyseisessä joukkueessa on 52,22 %.
Kaikissa muissa peleissä tarkastelin voittolinjoja ja vähensin niistä voiton todennäköisyyden laskemiseksi. Seuraava taulukko näyttää kuitenkin kunkin osapelin voittotodennäköisyyden.
William Hill Parlay -kortti
| Jalka | Reilun viinin | Todennäköinen voitto |
|---|---|---|
| Saints -8.5 | -7,5 | 47,78 % |
| Viikingit +8.5 | 8.5 | 52,22 % |
| Hou | -135 | 57,45 % |
| Laskut | 135 | 42,55 % |
| Patriootit | -205 | 67,21 % |
| Titaanit | 205 | 32,79 % |
| Meri | -118 | 54,13 % |
| Phil | 118 | 45,87 % |
| LSU | -200 | 66,67 % |
| Clemson | 200 | 33,33 % |
| AFC | -130 | 56,52 % |
| NFC | 130 | 43,48 % |
Kaksi valintaa, joilla on parhaat mahdollisuudet voittaa vaiheessa 1, ovat Patriots ja LSU. Tässä on suosittelemieni valintani voittotodennäköisyys:
- Viikingit +8,5 — 52,22 %
- Patriotit — 67,21 %
- LSU — 66,67 %
Näiden todennäköisyyksien tulo on 23,40 %. Jos saat 4 yhden vieraan ...
Ajattelin luoda sivupanoksen "push 22" -blackjack-muunnelmille, joka maksaisi 11:1, jos jakajalla olisi 22. Mitkä olisivat kertoimet?
Ajattelin luoda sivupanoksen "push 22" -blackjack-muunnelmille, joka voittaisi, jos jakajalla olisi 22. Millä kertoimilla sen pitäisi maksaa ja mikä olisi talon etu?
Olettaen, että jakaja nosti aina kätensä ulos (vaikka jokainen pelaaja olisi jo mennyt yli), osoitan, että todennäköisyys mennä yli 22:lla on 7,88 %, jos jakaja jää pehmeällä 17:llä, ja 8,00 %, jos hän saa pehmeän 17:n.
Olettaen, että jakaja saa pehmeän 17, voitolla 11:1 talon etu olisi 4,04 %. Kertoimella 10:1 se nousee 12,04 %:iin.
Minun pitäisi varoittaa teitä ja neuvoa pelaajia, että tämä olisi laskettavaa (ole hiljaa, Wiz!).
Amy ja Bob kilpailevat siitä, kuka voittaa ensimmäisenä neljä tasapeliä. Amy haluaa lyödä vetoa itsestään 8 000 dollarilla voittaakseen kilpailun. Hän voi kuitenkin lyödä vetoa vain yhdestä kolikonheitosta kerrallaan. Kaikki vedot maksavat tasapelin. Miten hän voi jäsentää vetonsa niin, että hän voittaa 8 000 dollaria, jos hän voittaa koko sarjan, ja häviää 8 000 dollaria, jos Bob voittaa?
Klikkaa alla olevaa painiketta nähdäksesi vastauksen.
Sarjan keskivaiheilla on 16 mahdollista tilaa. Seuraava taulukko näyttää Amyn tulisi asettaa panoksen kussakin tilassa ja hänen saldonsa ennen tätä strategiaa noudattavaa vetoa.
Vastaus
| Amy | Bob | Saldo | Veto |
|---|---|---|---|
| 0 | 0 | 0 | 2500 |
| 0 | 1 | -2500 | 2500 |
| 0 | 2 | -5000 | 2000 |
| 0 | 3 | -7000 | 1000 |
| 1 | 0 | 2500 | 2500 |
| 1 | 1 | 0 | 3000 |
| 1 | 2 | -3000 | 3000 |
| 1 | 3 | -6000 | 2000 |
| 2 | 0 | 5000 | 2000 |
| 2 | 1 | 3000 | 3000 |
| 2 | 2 | 0 | 4000 |
| 2 | 3 | -4000 | 4000 |
| 3 | 0 | 7000 | 1000 |
| 3 | 1 | 6000 | 2000 |
| 3 | 2 | 4000 | 4000 |
| 3 | 3 | 0 | 8000 |
Napsauta alla olevaa painiketta nähdäksesi ratkaisun.
Olkoon:
- a = Amy voittaa
- b = Bob voittaa
- w = Amyn nettovoitto sarjassa tähän mennessä
- f(a,b,w) = Amyn panoskoko seuraavassa pelissä
Tällaisissa pulmapeleissä on yleensä hyvä strategia aloittaa ja lopettaa ja työskennellä loppuun asti. Tästä huolimatta on helppo nähdä, että:
f(3,3,0) = 8 000
Tässä tilanteessa seitsemäs peli on "voittaja vie kaiken". Amyn voittosumman tulisi olla 0, ja hänen tulisi panostaa 8 000 viimeiseen käännökseen, mikä antaa hänelle 8 000 voittoa, jos hän voittaa käännöksen, ja 8 000 tappiota muuten.
Palataanpa askel taaksepäin. Entä jos hänellä on 3 voittoa ja Bobilla 2. Jos hän voittaa seuraavan flipin, hän voittaa koko pelin. Jos hän häviää, hänen tuloksensa on 3-3. Yhtälöstä f(3,3,0) hänellä pitäisi olla 0, jos tulos on 3,3. Joten hänen on saatava 8 000, jos hän voittaa seuraavan flipin, ja 0 muussa tapauksessa. Tässä tapauksessa nettovoitto on noin 4 000 ja panos on sama. Joten:
f(3,2,4000)=4 000
Palataanpa vielä askel taaksepäin. Entä jos hänellä on 3 voittoa ja Bobilla 1. Jos hän voittaa seuraavan flipin, hän voittaa koko pelin. Jos hän häviää, hänen tuloksensa on 3-2. Yhtälöstä f(3,2,4000) päädymme siihen, että hänellä pitäisi olla 4 000, jos tulos on 3,2. Joten hänen on saatava 8 000, jos hän voittaa seuraavan flipin, ja 4 000 muussa tapauksessa. Tässä tapauksessa nettovoitto on keskellä [(4 000 + 8 000) / 2 = 6 000] ja panos on puolet näiden kahden maalin välisestä etäisyydestä, [(8000-4000) / 2 = 2000]. Joten:
f(3,1,6000) = 2 000
Palataanpa vielä askel taaksepäin. Entä jos hänellä on 3 voittoa ja Bobilla 0. Jos hän voittaa seuraavan flipin, hän voittaa koko pelin. Jos hän häviää, hänen tuloksensa on 3-1. Yhtälöstä f(3,1,6000) päädymme siihen, että hänellä pitäisi olla 6 000, jos tulos on 3,1. Joten hänen on saatava 8 000, jos hän voittaa seuraavan flipin, ja 6 000 muussa tapauksessa. Tässä tapauksessa nettovoitto on keskellä [(6 000 + 8 000) / 2 = 7 000] ja panos on puolet näiden kahden maalin välisestä etäisyydestä, [(8000-4000) / 2 = 2000]. Joten:
f(3,0,7000) = 1 000
Toivottavasti on selvää, että Amyn nettovoitto olisi 0, jos tilanne joskus tasan. Tasapelitilanteessa hänen todennäköisyytensä voittaa koko sarja on 50 %. Jos maalien tasapaino on 8 000 voittoa/tappiota kummassakin tapauksessa, hänen on panostettava kertoimella 0 tai hänellä on mahdollisuus, ettei hän saavuta kumpaakaan loppumaalia.
Seuraavaksi, jos Amy on joskus sarjassa tappiolla, hänen nettovoittonsa pitäisi olla -1 kertaa se nettovoitto, joka syntyisi, jos hän olisi samalla pistemäärällä edellä. Tarkastellaan esimerkiksi tulosta Amy 2 - Bob 3 (tai 2-3). Jos hän häviää seuraavan flipin, hän häviää koko pelin. Jos hän voittaa, hänen tuloksensa on 3-3. Yhtälöstä f(3,3,0) päätellen hänellä pitäisi olla 0, jos tulos on 3,3. Joten hänen tuloksensa on oltava 0, jos hän voittaa seuraavan flipin, ja -8000 muuten. Tässä tapauksessa nettotappio on noin 4 000 ja panos on sama. Joten:
f(2,3,-4000)=4 000
Samalla logiikalla:
f(1,3,-6000) = 2 000
f(0,3,-7000) = 1 000
Seuraavaksi, mikä Amyn tulisi panostaa, jos tulos on 2-2? Jos hän voittaa flipin, tulos on 3-2. Yllä olevasta näemme, että hänen on voitettava netto 4 000 tällä tuloksella. Näemme myös, että jos hän on tappiolla 2-3, hänen nettotappionsa on oltava 4 000. Näin ollen hänen on panostettava 4 000:
f(2,2,0) = 4 000
Palataanpa siitä askeleen taaksepäin, entä jos tilanne on 2-1? Olemme määrittäneet, että hänen on voitettava 6 000 pistettä, jos hän voittaa seuraavan flipin (tulos 3-1), ja 0 pistettä, jos hän häviää (tulos 2-2). Tässä tapauksessa nettovoitto on keskellä [(6 000 + 0) / 2 = 3 000] ja panos on puolet näiden kahden maalin välisestä etäisyydestä, [(6 000 - 0) / 2 = 3 000]. Joten:
f(2,1,3000) = 3000
Palataanpa siitä vielä askeleen taaksepäin. Entä jos hänellä on kaksi voittoa ja Bobilla ei yhtään. Jos hän voittaa seuraavan volatiosuuden, tilanne on 3-0. Jos hän häviää, tilanne on 2-1. Hänen pitäisi saada 7000 nettovoittoa 3-0-tilanteessa ja 3000 2-1-tilanteessa. Tilanteella 2-0 saadaan nettovoitto keskeltä [(7 000 + 3 000) / 2 = 5 000] ja panos, joka on puolet näiden kahden maalin välisestä etäisyydestä, [(7000-3000) / 2 = 2 000]. Joten:
f(2,0,5000) = 2000
Kääntämällä ne pisteet, joissa Alicella on kaksi voittoa ja Bobilla vähemmän, tiedämme myös:
f(1,2,-3000) = 3000
f(0,2,-5000) = 2000
Kuten aiemmin selitettiin, Amyn nettovoiton pitäisi olla 0, jos sarja on tasainen, joten 1–1-tilanteessa hänen nettovoittonsa pitäisi olla 0. 2–1-tilanteessa hänen on oltava 2 000 johdossa ja 1–2-tilanteessa hänen on oltava 2 000 tappiolla. Näin ollen tasatilanteessa 1–1 hänen tulisi panostaa 2 000 eli:
f(1,1,0) = 2 000
Entä jos Amy johtaa 1–0? Olemme päättäneet, että hänen on oltava 5 000 johdossa kertoimella 2,0. Tilanteella 1–1 hänen on oltava tasoissa.Tilanteesta 1–0 saadaan nettovoitto keskeltä maalialueelta [(5 000 + 0) / 2 = 2 500] ja veto, joka on puolet näiden kahden maalin välisestä etäisyydestä, [(5 000–0) / 2 = 2 500]. Joten:
f(1,0,2500) = 2 500
Kääntämällä tilanteeksi 0-1:
f(0,1, -2500) = 2 500
Joten vihdoin olemme ensimmäisessä pelissä tilanteessa 0-0. Amyn on oltava 2 500 plussalla, jos hän voittaa seuraavan flipin, ja 2 500 miinuksella, jos hän häviää sen. Näin ollen 2 500 panos riittää. Tai:
f(0,0,0) = 2 500
Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .
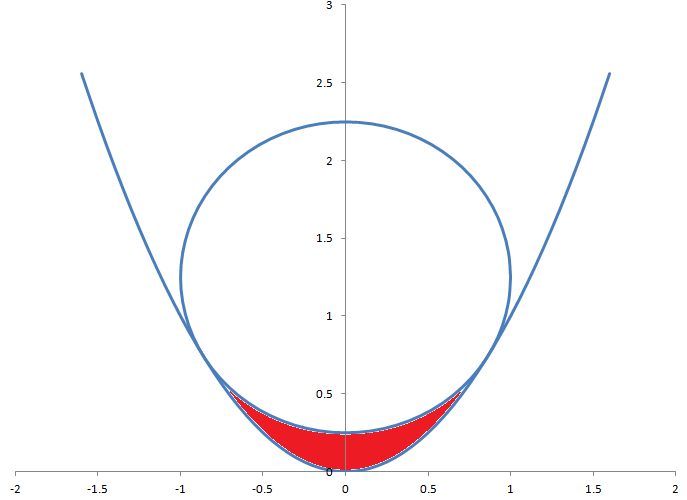
Säteeltään 1 oleva ympyrä on tangentti yhtälön y=x 2 mukaiselle paraabelille. Mikä on punaisella merkityn alueen pinta-ala ympyrän ja paraabelin välissä?
Klikkaa alla olevaa painiketta nähdäksesi vastauksen.
Tässä on ratkaisuni . (PDF)
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Sain tämän ongelman Presh Talwalkerilta Mind Your Decisionsista .


