WOO logo

Velho suosittelee

Kysy velholta #326

Mikä on Iron Cross -strategia crapsissa ja mitä mieltä olet siitä?

anonyymi

Rautaristi on tapa lyödä vetoa kentästä ja asettaa panoksia voittaakseen millä tahansa nopanheitolla paitsi numerolla 7. Kenttä kattaa jo numerot 2, 3, 4, 9, 10, 11 ja 12. Pelaaja lisää tähän panokset numeroille 5, 6 ja 8 kattaakseen loput numerot numeron 7 lisäksi. Seuraava taulukko näyttää, miltä laskutoimitukset näyttävät 5 dollarin panoksella kenttään, 5 dollarin panoksella numeroon 5 ja 6 dollarin panoksella numeroihin 6 ja 8.

Rautaristi

Noppien kokonaismäärä Voittaa Yhdistelmät Todennäköisyys Palata
2 10 1 0,027778 0,277778
3 5 2 0,055556 0,277778
4 5 3 0,083333 0,416667
5 2 4 0.111111 0.222222
6 2 5 0.138889 0,277778
7 -22 6 0,166667 -3,666667
8 2 5 0.138889 0,277778
9 5 4 0.111111 0,555556
10 5 3 0,083333 0,416667
11 5 2 0,055556 0,277778
12 15 1 0,027778 0,416667
36 1.000000 -0,250000

Taulukon oikeassa alakulmassa näkyy odotettu tappio 0,25 dollaria. Kokonaispanos on 22 dollaria. Tämä tekee talon eduksi 0,25 dollaria / 22 dollaria = 1/88 = 1,14 %.

Tässä vaiheessa saatat miettiä, miten tämä talon etu voi olla pienempi kuin yksittäisen panoksen talon etu. Vastaus on, että talon etu, joka on 1,52 % numeroille 6 ja 8 sekä 4,00 % numerolle 5, perustuu ratkaistuun panokseen. Jos talon etu määritellään panosten osalta heittokohtaisesti, talon etu numeroille 6 tai 8 on 0,46 % ja numerolle 5 1,11 %.

Voimme päätellä 1,14 %:n talon edun ottamalla kaikkien tehtyjen panosten painotetun keskiarvon seuraavasti:

(5 dollaria * 2,78 % + 5 dollaria * 1,11 % + 12 dollaria * 0,46 %) / 22 = 0,25 dollaria / 22 dollaria = 1,14 %.

Ole varovainen kasinoiden suhteen, jotka maksavat kenttäpanokselle vain 2:1 kertoimella 12. Vaadi täyttä 3:1-kerrointa. Lyhyempi voitto kaksinkertaistaa talon edun kyseisessä panoksessa 2,78 prosentista 5,56 prosenttiin.

Mielestäni 1,14 % on melko hyvä panos verrattuna useimpiin peleihin. Crapsissa voisi kuitenkin pärjätä paljon paremmin. Esimerkiksi 3-4-5x kertoimilla ja asettamalla sekä pass- että come-panokset täysillä kertoimilla talon etu voi laskea 0,37 %:iin. Päinvastoin, panostamalla don't pass- ja don't come -käskyt ja asettamalla täysillä kertoimilla, talon etu on 0,27 %.

Kuinka monta kertaa reilua noppaheittoa odotetaan tapahtuvan niin, että jokainen sivu on vähintään kaksi kertaa oikeassa paikassa?

Ace2

Vastaus on 390968681 / 16200000 = noin 24.13386919753086

Vaikka tämä voitaisiin ratkaista pitkällä ja työläällä Markov-ketjulla, pidän parempana integraaliratkaisua. Selitän, kuinka tätä menetelmää käytetään Fire Bet- ja Bonus Craps -sivuillani.

Kuvittele, että merkittävien tapahtumien yksi kerrallaan määrittämisen sijaan nopanheitto voi tarkoittaa yksittäisiä hetkiä. Oletetaan, että tapahtumien välinen aika ei kata muistia ja että tapahtumien välinen keskimääräinen aika on yksi aikayksikkö. Toisin sanoen tapahtumien välinen aika noudattaa eksponentiaalista jakaumaa, jonka keskiarvo on 1. Tällä ei ole merkitystä vedon ratkaisemisen kannalta, koska tapahtumat tapahtuvat edelleen yksi kerrallaan.

Poissonin jakauman mukaan todennäköisyys sille, että mitä tahansa nopan sivua on heitetty nolla kertaa x aikayksikössä, on exp(-x/6)*(x/6) 0 /0! = exp(-x/6). Poissonin jakauman mukaan todennäköisyys sille, että mitä tahansa sivua on heitetty tasan kerran, on exp(-x/6)*(x/6) 1 /1! = exp(-x/6) * (x/6). Näin ollen todennäköisyys sille, että mitä tahansa sivua on heitetty kaksi tai useampia kertoja x aikayksikössä, on 1 - exp(-x/6)*(1 + (x/6)). Todennäköisyys sille, että kaikki kuusi sivua on heitetty vähintään kaksi kertaa, on (1 - exp(-x/6)*(1 + (x/6))) 6. Todennäköisyys sille, että ainakin yhtä sivua ei ole heitetty vähintään kaksi kertaa, on yhtä suuri kuin:

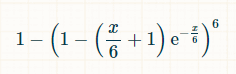
rullaa joka puolelta kahdesti

Meidän on integroitava se koko ajan, jotta löydämme, kuinka paljon aikaa keskimäärin kuluu, jos haluttua tavoitetta ei ole saavutettu.

Onneksi voimme tässä vaiheessa käyttää integraalilaskuria . Linkitettyä laskuria varten kirjoita 1- (1 - exp(-x/6)*(1 + x/6))^6 dx = apx. 24.1338692 tekstikenttään "Laske :n integraali" ja aseta mukautettu-kohdasta integroinnin rajaksi 0:sta ∞:aan.

Vastaus on 390968681 / 16200000 = noin 24,13386919753086

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Minulla on kaksiosainen kysymys.

Osalle 1 annettu:
  • x + y + z = 1
  • x^2 + y^2 + z^2 = 4
  • x^3 + y^3 + z^3 = 9

Mikä on x^4 + y^4 + z^4?

Toisen osan osalta, mikä on vastaus yleiseen tapaukseen, kun:

  • x + y + z = a
  • x^2 + y^2 + z^2 = b
  • x^3 + y^3 + z^3 = c

anonyymi

Kysymys 1: 97/6 = noin 16,166666

Kysymys 2: a 4 /6 + (4/3)ac - a 2 b + b 2 /2

Katso ratkaisuni (PDF)

Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .

Aloitat reilun kokoisella kuusisivuisella nopalla ja heität sitä kuusi kertaa ja kirjaat jokaisen heiton tulokset muistiin. Sitten kirjoitat nämä numerot toisen, nimeämättömän reilun kokoisen nopan kuudelle sivulle. Esimerkiksi, jos kuusi heittoasi olivat 3, 5, 3, 6, 1 ja 2, toisessa nopassasi ei olisi numeroa 4; sen sijaan siinä olisi kaksi numeroa 3.

Seuraavaksi heität tätä toista noppaa kuusi kertaa. Ota nämä kuusi numeroa ja kirjoitat ne seuraavan reilusti nopan sivuille ja jatkat tätä prosessia, jossa luot uuden nopan edellisestä.

Lopulta sinulla on noppa, jonka kaikilla kuudella sivulla on sama numero. Mikä on keskimääräinen siirtymien määrä nopasta toiseen (tai heittojen kokonaismäärä jaettuna kuudella), jotta saavutetaan tämä tila?

rsactuary

Noin 9.65599148388557

Merkitään alkuperäinen noppa kirjaimilla numeroiden sijaan sekaannusten välttämiseksi. Merkitään jokainen mahdollinen nopan tila kirjaimilla. Esimerkiksi AAABBBC tarkoittaisi kolmea yhdestä kirjaimesta, kahta toisesta ja yhtä kolmannesta. Alkutila olisi luonnollisesti ABCDEF.

Olkoon E(ABCDEF) odotettu heittojen lukumäärä tilasta ABCDEF.

P 10800 × E(AABCDE) + 720 × E(ABCDEF)]/46656

Seuraava siirtymämatriisi näyttää, kuinka monella tavalla kustakin alkutilasta (vasen sarake) uuteen tilaan voi siirtyä, perustuen tilasta toiseen siirtymisen yhdistelmien määrään. Tämän rakentaminen vei muuten muutaman tunnin.

Siirtymämatriisi A

Osavaltio
Ennen		 AAAAAAA AAAAAB AAAABB AAAABBB AAAABC AAAABC AABBCC AAABCD AABBCD AABCDE ABCDEF
AAAAAB 15 626 18 780 9 750 2 500 - - - - - - -
AAAABB 4 160 13 056 19 200 10 240 - - - - - - -
AAAABBB 1 458 8 748 21 870 14 580 - - - - - - -
AAAABC 4 098 12 348 8 190 2 580 7 920 10 080 1 440 - - - -
AAAABC 794 5 172 8 670 5 020 6 480 17 280 3 240 - - - -
AABBCC 192 2 304 5 760 3 840 5 760 23 040 5 760 - - - -
AAABCD 732 4 464 4 140 1 680 7 920 14 400 2 520 4 320 6 480 - -
AABBCD 130 1 596 3 150 1 940 5 280 16 800 3 600 4 800 9 360 - -
AABCDE 68 888 1 380 760 3 960 11 520 2 520 7 200 14 040 4 320 -
ABCDEF 6 180 450 300 1 800 7 200 1 800 7 200 16 200 10 800 720

En aio mennä pitkälle luennolle matriisialgebrasta, paitsi että sanotaan vaikka, että matriisi B on seuraava:

Matriisi B

Osavaltio
Ennen		 AAAAAB AAAABB AAAABBB AAAABC AAAABC AABBCC AAABCD AABBCD AABCDE ABCDEF
AAAAAB -27876 9750 2500 0 0 0 0 0 0 -46656
AAAABB 13056 -27456 10240 0 0 0 0 0 0 -46656
AAAABBB 8748 21870 -32076 0 0 0 0 0 0 -46656
AAAABC 12348 8190 2580 -38736 10080 1440 0 0 0 -46656
AAAABC 5172 8670 5020 6480 -29376 3240 0 0 0 -46656
AABBCC 2304 5760 3840 5760 23040 -40896 0 0 0 -46656
AAABCD 4464 4140 1680 7920 14400 2520 -42336 6480 0 -46656
AABBCD 1596 3150 1940 5280 16800 3600 4800 -37296 0 -46656
AABCDE 888 1380 760 3960 11520 2520 7200 14040 -42336 -46656
ABCDEF 180 450 300 1800 7200 1800 7200 16200 10800 -46656

Vastaus on matriisin B determinantin ja matriisin A determinantin suhde:

Määritä(A) = 1 461 067 501 120 670 000 000 000 000 000 000 000 000 000 000 000

Määritä(B) = 14 108 055 348 203 100 000 000 000 000 000 000 000 000 000 000

Määritä(B) / Määritä(A) = noin 9,65599148388557