WOO logo

Velho suosittelee

Kysy velholta #335

Luin Wizard of Vegas -artikkelistasi Reversible Royal -pelistä, jonka tuotto on 105,22 % . Tuo tuotto olettaa optimaalisen strategian, korttien järjestys mukaan lukien. Mikä on tuotto, jos oletan keskimääräisen Royal-voiton? Entä jos käytän tavallista 6-5 Bonus Poker -strategiaa, joka on perusmaksutaulukko?

anonyymi

Olettaen, ettei strategiasta poikkeamia, yksi 60:stä kuninkaallisesta on peräkkäinen. Käännettävä kuninkaallinen jättipotti maksaa 161 556 yhdestä. Mikä tahansa muu kuninkaallinen maksaa 800 yhdestä. Keskimääräinen kuninkaallinen voitto on siis (1/60) * 161 556 + (59/60) * 800 + 17 396 yhdestä.

Jos oletamme, että kaikki kuninkaalliset maksavat 17 396 ja pelaamme optimaalista strategiaa kyseisen kuninkaallisen voiton perusteella, niin tuotto laskee 103,56 prosenttiin.

Jos pelaamme perusmaksutaulukkoa vastaavaa 6-5 Bonus Poker -strategiaa, tuotto laskee edelleen 101,97 prosenttiin.

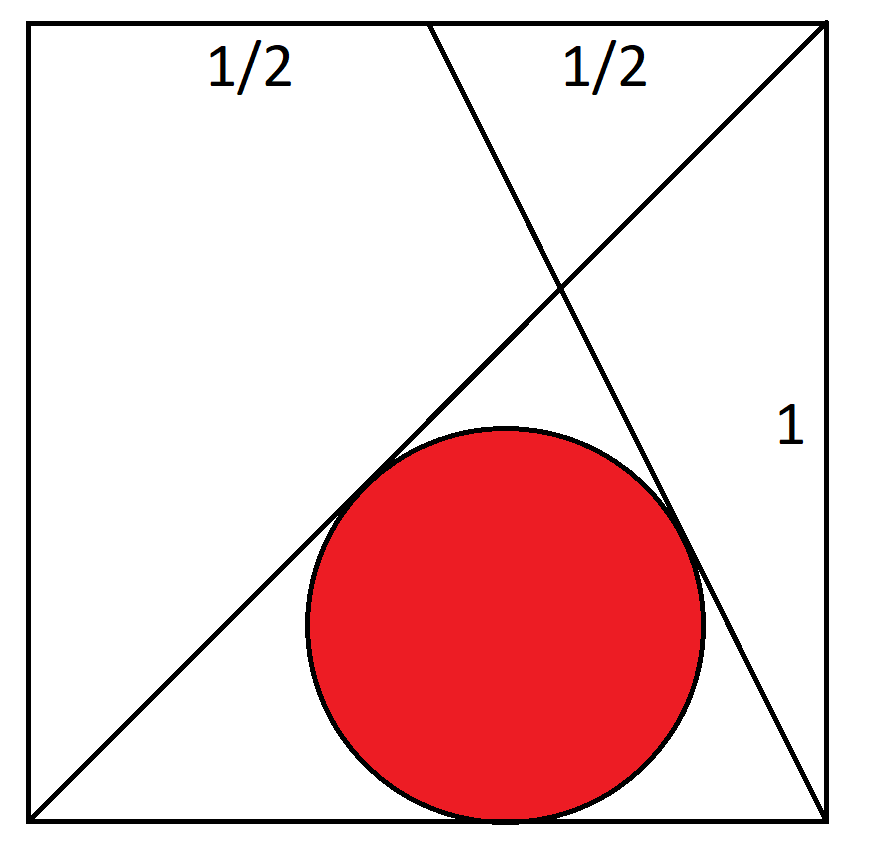
Tarkastellaan yksikköneliötä, jonka koordinaatit ovat (0,0), (1,0), (1,1), (0,1). Suora A kulkee pisteestä (0,0) pisteeseen (1,1). Suora B kulkee pisteestä (1,0) pisteeseen 0,5,1). Mikä on ympyrän säde, joka on tangentti suorille A, B ja ympyrän pohjalle?

Tämä pulmapeli ilmestyi Mensa Bulletinin lokakuun 2020 numerossa.

anonyymi

rusketus(2x)=2rusketus(x)/(1-rusketus 2 (x))[/spoileri]

[spoiler=Vastaus]Vastaus on (1+neliöyksikkö(2)+neliöyksikkö(5)-neliöyksikkö(10))/6 = noin 0,248000646617418.

Tässä on ratkaisuni (PDF).

Tätä ongelmaa on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Mikä on todennäköisyys saada Yahtzee, jos se on ainoa jäljellä oleva kategoria kortilla?

anonyymi

Niille lukijoille, jotka eivät tunne Yahtzeea, kysymys kuuluu, mikä on todennäköisyys saada viisi samaa kolmella viiden nopan heitolla. Jokaisen heiton jälkeen sinun on valittava, mitä noppia pidät kiinni ja mitkä nopat heität uudelleen.

Vastaus on 4,6029 %.

[spoiler=Ratkaisu]

Tässä ovat mahdolliset tulokset ensimmäisen heiton jälkeen tai minkä tahansa heiton jälkeen, jossa pelaaja heittää 4 tai 5 noppaa.

  • Viisi samaa = 6*(1/6)^5 = 0,000772
  • Neloset = (1/6)^3*(5/6)*4 = 0,015432
  • Kolmoset = (1/6)^2*(5/6)^2*KOMBIN(4,2) = 0,115741
  • Kaksi samaa = 4*(1/6)*(5/6)^3 = 0,385802
  • Ainutlaatuinen = 6*5!/6^5 = 0.092593

Tässä ovat todennäköisyydet parin pitämisen jälkeen.

  • Viisi samaa =(1/6)^3 = 0,004630
  • Neloset = 3*(1/6)^2*(5/6) = 0,069444
  • Kolmoset = 3*(1/6)*(5/6)^2+5*(1/6)^3 = 0,370370
  • Kaksi samaa = (5/6)^3 - 5 * (1/6)^3 = 0,555555

Tässä ovat todennäköisyydet kolmen samanlaisen kädessä pitämisen jälkeen:

  • Viisi samaa =(1/6)^3 = 0,002778
  • Neloset = 2 * (1/6) * (5/6) = 0,27778
  • Kolmoset = (5/6)^2 = 0,694444

Tässä ovat todennäköisyydet nelosten jälkeen:

  • Viisi samaa =1/6 = 0,166667
  • Neloset = 5/6 = 0,83333

Näillä etenemistodennäköisyyksillä tässä ovat kunkin tilan todennäköisyydet toisen heiton jälkeen:

  • Viisi samaa = 0,000772 + 0,015432*0,166667 + 0,115741*0,002778 + 0,385802*0,004630 + 0,092593* 0,000772 = 0,012631
  • Neloset = 0,015432 * 0,166667 + 0,115741 * 0,27778 + 0,115741 * 0,27778 = 0,116970
  • Kolmoset = 0,115741 * 0,694444 + 0,385802 * 0,370370 + 0,092593 * 0,115741 = 0,409022
  • Kaksi samanlaista = 0,385802 * 0,555555 + 0,092593 * 0,385802 = 0,450103
  • Ainutlaatuinen = 0,092593 * 0,092593 = 0,008573

Käyttämällä samoja etenemistodennäköisyyksiä, tässä on Yahtzeen todennäköisyys kolmannen heiton jälkeen:

Viisi samaa = 0,012631 + 0,116970*(1/6) + 0,409022*(1/6)^2 + 0,450103*(1/6)^3 + 0,008573*(1/6)^4 = 0,046029.

Niille teistä, jotka pitävät matriisialgebrasta, on olemassa siirtymämatriisi:

0,092593 0.694444 0.192901 0,019290 0,000772
0.000000 0,555556 0.370370 0,069444 0,004630
0.000000 0.000000 0.694444 0,277778 0,027778
0.000000 0.000000 0.000000 0,833333 0,166667
0.000000 0.000000 0.000000 0.000000 1.000000

Jos yllä oleva matriisi on M, niin tila kolmen heiton jälkeen on M3 seuraavasti:

0,000794 0.256011 0,452402 0,244765 0,046029
0.000000 0,171468 0.435814 0.316144 0,076575
0.000000 0.000000 0,334898 0.487611 0,177491
0.000000 0.000000 0.000000 0.578704 0,421296
0.000000 0.000000 0.000000 0.000000 1.000000

Todennäköisyys saada Yahtzee kolmen heiton jälkeen löytyy oikeassa yläkulmassa olevasta solusta.

[/spoileri]

Katsottuani läpi The Queen's Gambitin huomasin, ettei yksikään ohjelman peleistä päättynyt tasapeliin. Luulin, että shakissa korkeilla tasoilla on paljon tasapelejä. Kuinka monta prosenttia peleistä päättyy tasapeliin suurmestaritason shakissa?

anonyymi

ChessBase.com-sivuston artikkelin Has the number of draws in shacks increased? mukaan kirjoittaja Qiyu Zhou toteaa, että 78 468:ssa pistemäärältään 2600 tai sitä korkeamman pistemäärän (suurmestariksi vaaditaan 2500 pistettä) pelatussa pelissä tulokset olivat seuraavat:

  • Musta voittaa: 18,0 %
  • Valkoiset voittavat: 28,9 %
  • Tasapeli: 53,1 %