Kysy velholta #336

Tämä on hyvä pelaajalle! Heidän verkkosivunsa ei kerro yksityiskohtia tarkemmin, joten oletan sen koskevan vain kahta ensimmäistä korttia. Näen vanhassa Current Blackjack -uutiskirjeessäni lokakuulta 2018, että useimmissa pöydissä on seuraavat säännöt:

• Jakaja osuu pehmeään 17:ään
• Kuusi pakkaa
• Blackjack maksaa 3:2
• Tuplaus splitin jälkeen sallittu
• Ässien uudelleenjako sallittu

Blackjackin talon edun laskurini sanoo, että näiden sääntöjen mukaan talon etu on 0,55 % jatkuvalla sekoittajalla ja 0,57 % jaetulla kortilla.

Säännöistä riippumatta todennäköisyys saada kova 16 kahdella ensimmäisellä kortilla on 6,51 %. Jos saat 16 dollaria 6,51 %:n todennäköisyydellä, se on 1,04 dollaria kättä kohden. Oletan minimipanoksen olevan 25 dollaria, koska useimmat kasinot nostavat minimipanoksiaan koronavirusaikakaudella. Bonusta lukuun ottamatta odotettu tappio kättä kohden on 0,14 dollaria 25 dollarin panoksella. Tämä tekee odotetusta voitosta kättä kohden 1,04 dollaria - 0,14 dollaria = 0,90 dollaria. Suhteessa panossummaan tämä on 3,59 %:n etu pelaajaa kohden!

Jos oletamme hyvän skenaarion, jossa pelataan kolme 25 dollarin kättä 80 kierroksen tuntinopeudella, odotettu tuntivoitto olisi 216 dollaria!

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

[spoiler=Ratkaisu]

Ensinnäkin, tapuille on combin(25,3) = 2 300 mahdollista yhdistelmää.

Kuinka moni näistä yhdistelmistä muodostaa kolmion? Käytetään tätä lautaa apuna:

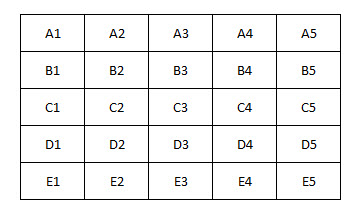
Ensinnäkin on viisi riviä, viisi saraketta ja kaksi lävistäjää. Jokaiselle niistä on combin(5,3) = 10 tapaa sijoittaa tapit riviin. Joten kombinaatioita on 12 * 10 = 120 tällä tavalla.

Toiseksi, rivin/sarakkeen keskimmäisen neliön voi yhdistää viereisen rivin/sarakkeen keskimmäiseen neliöön neljällä eri tavalla. Toisin sanoen, nämä kolme sijoittelua:

• A3, B4, C5
• C5, D4, E3
• E3, D2, C1
• C1, B2, A3

Joten nyt olemme luvussa 120 + 4 = 124

Kolmanneksi, on neljä erilaista diagonaaliviivaa, jotka ovat neljä välilyöntiä:

• A2, B3, C4, D5
• B5, C4, D3, E2
• E4, D3, C2, B1
• D1, C2, B3, A4

Jokaiselle niistä on combin(4,3)=4 tapaa sijoittaa kolme tappia. Eli lisää tulee 4*4 = 16 lisää.

Olemme nyt luvussa 124 + 16 = 140

Neljänneksi, tarkastellaan ratsun liikkumista shakissa 2x1 L-muodossa. Jokaista kulmaa kohden on kaksi tapaa, joilla ratsu voi liikkua. Kaikissa näissä tapauksissa ratsu voi liikkua uudelleen samaa linjaa pitkin, josta se lähti ensimmäiselle siirrolle. Eli 4 * 2 = 8 lisää:

• A1, C2, E3 A1, B3, C5
• A5, B3, C1
• A5, C4, E3
• E5, C4, A3
• E5, D3, C1
• E1, D3, C5
• E1, C2, A3

Keskustan läpi kulkee myös neljä tällaista ritarilinjaa:

• A2, C3, E4
• A4, C3, E2
• B5, C3, D1
• D5, C3, B1

Yhteenlaskettuna 12 ritarilinjaa saadaan 140 + 12 = 152.

Jos yhdistelmiä on yhteensä 2 300 ja lomakeviivoja 152, niin 2300 - 152 = 2 148 eivät muodosta viivoja ja muodostavat siten kolmioita.

Näin ollen vastauksemme on 2 148/2 300 = 93,39 %.

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Yksinkertaisuuden vuoksi oletetaan, että ässän uudelleenjako ei ole sallittua. Muista myös, että Espanjan 21:ssä käytetään 48 kortin espanjalaisia pakkoja ilman kymppejä. Lopuksi, muista, että 21 pistettä on automaattinen voittaja Espanjan 21:ssä.

Vaikka kyseistä sääntöä ei olisikaan, pelaajan tulisi aina jakaa ässät. Ässäparin saamisen todennäköisyys neljän espanjalaisen pakan pelissä on combin(16,2)/combin(192,2) = 120/18336 = 0,65 %.

Todennäköisyys sille, että jokainen ässä saa 10, on (4 * 12) / (48 * 12 - 2) = 48/190 = 25,26 %. Kahdella ässällä blackjackeiksi muuttuvien lukujen odotusarvo on 2 * 48/190 = 96/190 = 0,5053.

Jokainen blackjack on arvoltaan puoli yksikköä lisää. Näin ollen tämän säännön arvo on (120/18336)*(96/190)*(1/2) = 0,17 %.

Tästä säännöstä huolimatta pelaajan ei pitäisi jakaa kymppejä, joten meidän ei tarvitse huolehtia siitä. Joten tämä sääntö pienentää talon etua 0,17 %.

[spoiler=Ratkaisu]

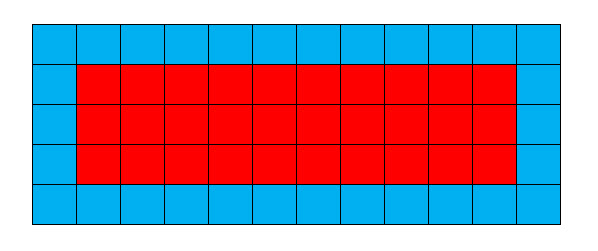
Olkoon x ja y SISÄISEN suorakulmion mitat.

Tuon suorakulmion pinta-ala on x * y.

Kehän pinta-ala on 2x + 2y + 4

Oletetaan, että xy = 2x + 2y + 4

xy-2x = 2y + 4

x(y-2) = 2y+4

x=(2y+4)/(y-2)

y:n on oltava suurempi tai yhtä suuri kuin 3. Katsotaanpa, mikä x on joillekin y:n arvoille, jotka ovat yhtä suuria tai suurempia kuin 3.

Jos y = 3, niin x = 10
Jos y = 4, niin x = 6
Jos y = 5, niin x = 14/3
Jos y = 6, niin x=4

Eli 3x10 ja 4x6 ovat ratkaisuja. 6x4 ei ole, koska se ei ole yksikäsitteinen ratkaisu. Kun y kasvaa, x pienenee. Aivan kuten y:n on oltava yhtä suuri tai suurempi kuin 3, niin myös x:n on oltava. Koska x pienenee y:n kasvaessa, on vain yksi mahdollinen arvo lisää x:lle, ja se on x=3. Jos x=3, niin y=10, eikä sekään ole yksikäsitteinen.

Joten vastaus on 2: 3x10 ja 4x6 sisemmälle suorakulmiolle. Jos haluat mieluummin laskea ratkaisut ulomman suorakulmion mukaan, ne olisivat 5x12 ja 6x8.

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .