Velho suosittelee
-
$11000 Welcome Bonus -
UP TO $777 BONUS -
$3000 Welcome Bonus
Kysy velholta #338
Kuinka monta heittoa keskimäärin tarvitaan kahdella nopalla, jotta saadaan kaikki yhteistulokset 2:sta 12:een?
[spoiler=Ratkaisu]
Tähän voisi käyttää Markov-ketjua, mutta pidän parempana differentiaali- ja integraalilaskentaa. Olennaista on, että vastaus on sama, jos heittojen välinen aika on eksponentiaalisesti jakautunut ja keskiarvo on yksi. Vastaus voidaan kuitenkin ilmaista integraalina nollasta äärettömyyteen:
1-(1-lauseke(-x/36))^2*(1-lauseke(-x/18))^2*(1-lauseke(-x/12))^2*(1-lauseke(-x/9))^2*(1-lauseke(-5*x/36))^2*(1-lauseke(-x/6))
Voit helposti ratkaista tällaiset integraalit integraalilaskimella .
Voit ratkaista minkä tahansa tällaisen ongelman myös odotettavissa olevien kokeiden laskurillani .
[/spoileri]Neliön keskellä on muurahainen. Se on 17 tuuman päässä vasemmasta yläkulmasta, 20 tuuman päässä oikeasta yläkulmasta ja 13 tuuman päässä oikeasta alakulmasta.
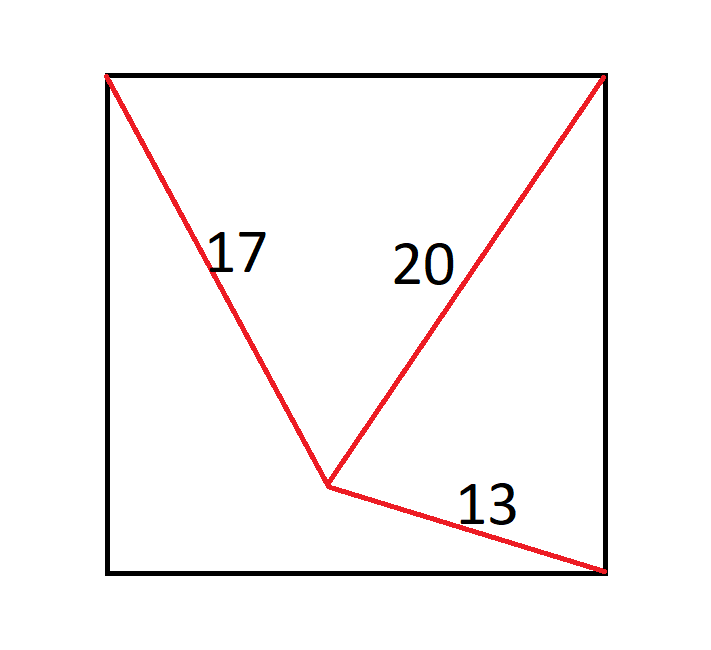
Kuinka suuri neliö on?
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)
[spoiler=Ratkaisu]
Kierrä ensin kolmiota ABE 90 astetta muodostaaksesi uuden kolmion BDF.
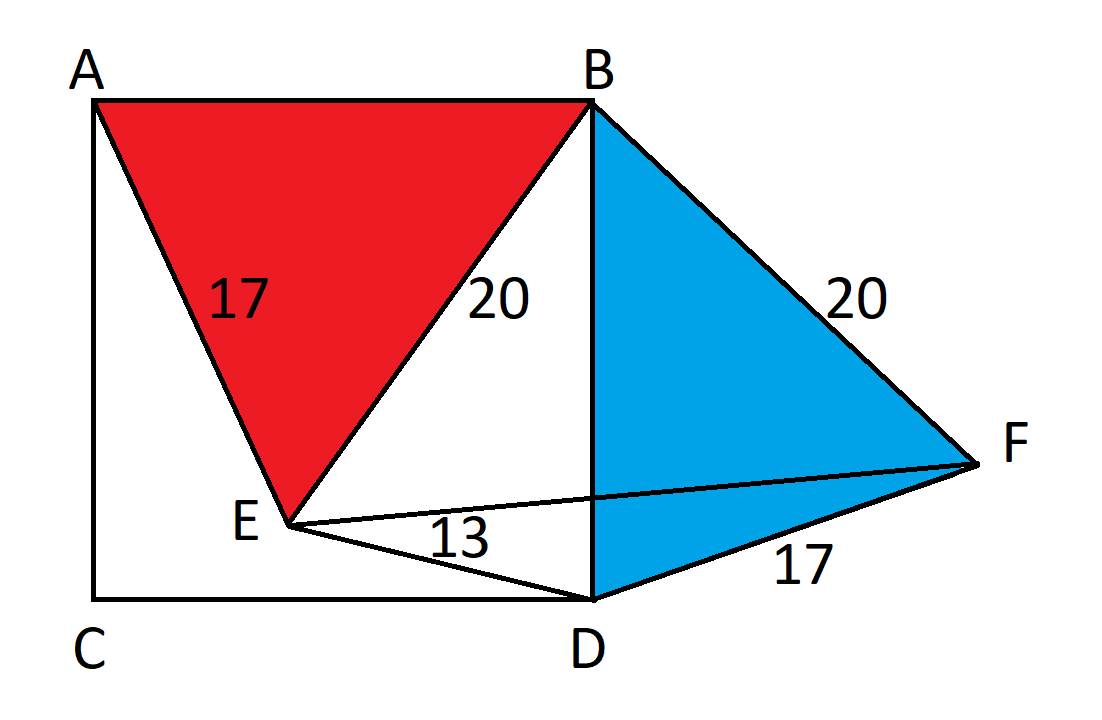
Koska kolmiota on kierretty 90 astetta, kulma EBF = 90, määritelmän mukaan. Pythagoraan kaavan mukaan EF = 20*sqrt(2).
Kosinien lain mukaan: 17^2 = 13^2 + (20*neliöjalka(2))^2 - 2*13*20*neliöjalka(2)*cos(DEF).
289 = 169 + 800 - 520 * neliöjuuri (2) * cos (DEF)
520 * neliöjuuri(2) * cos(DEF) = 680.
cos(DEF) = 17 * neliöjuuri(2) / 26.
Muista, sin^2(x) + cos^2(x) = 1. Käytetään sitä sin(DEF)-funktion ratkaisemiseen.
sin^2(DEF) + cos^2(DEF) = 1
sin^2(DEF) + (17*neliöyksikkö(2)/26)^2 = 1
sin^2(DEF) + 289/338 = 1
sin^2(DEF) = 49/338
sin(DEF) = 7 * neliöjuuri(2) / 26
Seuraavaksi tarkastellaan kulmaa BED.
Kulma BED = Kulma BEF + Kulma FED.
Tiedämme, että EBF on 90 astetta ja tasakylkinen kolmio. Se tekisi kulman BEF olevan 45 astetta.
Joten, kulma BED = 45 astetta + kulma FED.
Muista, cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b).
cos(BED) = cos(BEF + FED) = cos(BEF)*cos(FED) - sin(BEF)*sin(FED)
= (1/neliö(2))*17*neliö(2)/26 - (1/neliö(2))*7*neliö(2)/26
= (17/26) - (7/26) = 10/26 = 5/13
Sovelletaan kosinien lakia uudelleen, tällä kertaa kolmioon BED.
BD^2 = 20^2 + 13^2 - 2*20*13*(5/13)
= 400 + 169 - 200 = 369
BD on kyseisen neliön sivu, joten BD^2 on kyseisen neliön pinta-ala, jonka olemme osoittaneet olevan 369.
[/spoileri]Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Drop Dead on peli, jota pelataan viidellä tavallisella nopalla. Aloitat vuorosi heittämällä kaikki viisi noppaa. Jos mikään niistä ei ole 2 tai 5, lasket noppien summan yhteen, lisäät summan pistemäärääsi ja heität uudelleen. Jos heität mitkä tahansa 2 tai 5, heiton pistemäärä on nolla. Kaikki 2:ta tai 5:tä näyttävät nopat julistetaan kuolleiksi ja sivuun. Sitten heität uudelleen jäljellä olevilla nopilla. Peli jatkuu joko pisteiden keräämisellä tai noppien poistamisella. Vuorosi päättyy, kun kaikki noppasi on pudonnut, jolloin sinun sanotaan kuolleen. Kaikki pisteheittosi lasketaan yhteen lopulliseksi pistemääräksi. Korkea pistemäärä voittaa.
Mikä on odotettu tulos tässä pelissä?
[spoiler=Ratkaisu]
Aloitetaan skenaariolla, jossa on yksi noppa jäljellä, ja siirrytään taaksepäin.
Olkoon muuttuja a odotettu lisäpistemäärä, kun jäljellä on yksi noppa.
Keskimääräinen heitto, joka ei ole 2 tai 5, on (1 + 3 + 4 + 6) / 4 = 7/2.
a = (2/3) × (a + 7/2).
a/3 = 7/3.
a = 7.
Lasketaan seuraavaksi b, odotettu pistemäärä, kun jäljellä on kaksi noppaa.
b = (2/3) 2 × (b + 2 × (7/2)) + 2 × (2/3) × (1/3) × a.
b = 11,2.
Lasketaan seuraavaksi c, odotettu pistemäärä, kun jäljellä on kolme noppaa.
c = (2/3) 3 × (c + 3 × (7/2)) + 3 × (2/3) 2 × (1/3) × b + 3 × (2/3) × (1/3) 2 × b.
c = 1302/95 = 13,705263.
Lasketaan seuraavaksi d, odotettu pistemäärä, kun jäljellä on neljä noppaa.
d = (2/3) 4 × (d + 4 × (7/2)) + 4 × (2/3) 3 × (1/3) × c + 6 × (2/3) 2 × (1/3) 2 × b + 4 × (2/3) × (1/3) 3 × a.
d = 3752/247 = 15,190283.
Lopuksi lasketaan e, odotettu pistemäärä, kun jäljellä on viisi noppaa.
e = (2/3) 5 × (e + 5 × (7/2)) + 5 × (2/3) 4 × (1/3) × d + 10 × (2/3) 3 × (1/3) 2 × c + 10 × (2/3) 2 × (1/3) 3 × b + 5 × (1/3) × 4 × (1/3) ×.
e = 16,064662.
Tätä kysymystä on kysytty ja siitä keskusteltu foorumillani Wizard of Vegasissa .
[/spoileri]Tarkastellaan Pairplus-panosta Three Card Pokerissa, joka noudattaa voittotaulukkoa 1-4-6-30-40. Se kuitenkin maksaa jättipotin pata-minikuninkaalle ja 25 % tästä jättipotista kolmen muun maan minikuninkaalle. Kuinka korkealla mittarin täytyy olla, jotta panos olisi reilu?
Vastaus on 384 kertaa panossumma.
Jokaista 100 lisävetoa kohden tuotto kasvaa 0,79 %.
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .