WOO logo

Velho suosittelee

Kysy velholta #341

Kuinka monta kahden nopan heittoa tarvitaan, jotta saadaan jokainen yhteistulos 2:sta 12:een? Käytä ratkaisussasi differentiaali- ja integraalilaskentaa.

BruceZ

Noin 61.2173847639572 rullaa.

[spoiler=Ratkaisu]

Muista, että todennäköisyys sille, että heitetään yhteensä 2, on 1/36. T:llä heitolla odotettu heittojen määrä, joiden kokonaismäärä on 2, on t/36. Oletetaan, että heittojen välinen aika on eksponentiaalisesti jakautunut keskiarvon ollessa t/36. Poissonin jakauma kertoo meille, että todennäköisyys sille, että heitetään yhteensä 2, on exp(-t/36).

Muista, että todennäköisyys sille, että heitetään yhteensä 3, on 2/36 = 1/18. Samalla logiikalla Poisson-jakauma kertoo meille, että todennäköisyys sille, että heitetään yhteensä 3, on exp(-t/18).

Muista, että todennäköisyys sille, että heitetään yhteensä 4, on 3/36 = 1/12. Samalla logiikalla Poisson-jakauma kertoo meille, että todennäköisyys sille, että heitetään yhteensä 4, on exp(-t/12).

Muista, että todennäköisyys sille, että heitetään yhteensä 5, on 4/36 = 1/9. Samalla logiikalla Poisson-jakauma kertoo meille, että todennäköisyys sille, että heitetään yhteensä 5, on exp(-t/9).

Muista, että todennäköisyys sille, että heitetään lukuja yhteensä 6, on 5/36. Samalla logiikalla Poisson-jakauma kertoo meille, että todennäköisyys sille, että heitetään lukuja yhteensä 6, on exp(-5t/36).

Muista, että todennäköisyys sille, että heitetään yhteensä 7, on 6/36 = 1/6. Samalla logiikalla Poisson-jakauma kertoo meille, että todennäköisyys sille, että heitetään yhteensä 7, on exp(-t/6).

Todennäköisyydet luvuille 8–12 ovat samat kuin luvuille 2–6.

Näin ollen todennäköisyys sille, että jokaisesta kokonaisluvusta t yksikköä on heitetty ainakin kerran, on:

(1-op(-t/36))^2 * (1-op(-t/18))^2 * (1-op(-t/12))^2 * (1-op(-t/9))^2 * (1-op(-5t/36))^2 * (1-op(-t/6))

Todennäköisyys, että ainakin kokonaissummaa EI ole laskettu t aikayksikössä, on 1 - (1-lauseke(-t/36))^2 * (1-lauseke(-t/18))^2 * (1-lauseke(-t/12))^2 * (1-lauseke(-t/9))^2 * (1-lauseke(-5t/36))^2 * (1-lauseke(-t/6))

Saadaksemme odotetun ajan ilman yhtäkään kokonaislukua, integroimme yllä olevan funktion nollasta äärettömyyteen.

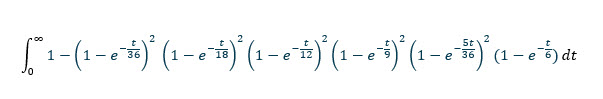
Integraalilaskuri (suosittelen tätä ) ratkaisee tämän helposti muodossa 769767316159/12574325400 = noin 61,2173847639572 rullaa.

[/spoileri]

Tätä kysymystä on kysytty ja siitä keskusteltu foorumillani Wizard of Vegasissa .

Heitä kahta noppaa, punaista ja sinistä noppaa, yhä uudelleen ja uudelleen. Pidä kirjaa kunkin nopan heittojen summasta. Mikä on odotettu roolien lukumäärä, kunnes nämä kaksi yhteissummaa ovat yhtä suuret?

teliot

Vastaus on ääretön.

[spoiler=Lisää kommentteja]

On vaikea selittää, miksi vastaus on ääretön. Asiaa hämmentää ja tekee paradoksaalisemmaksi se, että todennäköisyys sille, että kokonaissummat koskaan ovat yhtä suuret, on 1.

Seuraava taulukko näyttää todennäköisyyden sille, että kokonaisluvut ovat samat ensimmäistä kertaa 1–16 heiton jälkeen.

Todennäköisyys yhtä suurille kokonaistuloksille ensimmäistä kertaa

Rullat Todennäköisyys
1 0,166667
2 0.112654
3 0,092850
4 0,080944
5 0,072693
6 0,066539
7 0,061722
8 0,057819
9 0,054573
10 0,051819
11 0,049443
12 0,047367
13 0,045532
14 0,043895
15 0,042423
16 0,041089

Excel näyttää erittäin lähellä tätä käyrää olevan kaavan y = 0,1784*x-1,011, jossa x = heittojen lukumäärä ja y = todennäköisyys.

Tämän äärettömän sarjan summa on ääretön.

[/spoileri]

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Mikä on Pennsylvania Cash 5 -pelin kannattavuusrajalla oleva jättipotti? Voit jättää verot ja jättipotin jakamisen huomiotta.

100xOdds

Käydään ensin läpi säännöt. Panos on 2 dollaria. Peli perustuu viiden pallon nostamiseen 43 pallosta. Tässä on voittotaulukko:

  • Ottelu 5 = Jackpot
  • Matematiikka 4 = 200 dollaria
  • Ottelu 3 = 10 dollaria
  • Ottelu 2 = 2 dollaria

Lisäksi pelaaja saa oletettavasti raaputusarvan kaltaisen kortin. Voiton todennäköisyys on 1/80 ja voitto 2 dollaria 1/5.

Seuraava taulukko näyttää analyysini peruspelistä. Se osoittaa, että 2–4 numeron saamisen arvo on 0,287784 dollaria.

Cash 5 -palautustaulukko

Saalis Maksaa Yhdistelmät Todennäköisyys Palata
5 jättipotti 1 0.000001 ?
4 200 190 0,000197 0,039477
3 10 7030 0,007303 0,073032
2 2 84360 0,087638 0,175276
1 0 369075 0,383416 0.000000
0 0 501942 0,521445 0.000000
Kokonais 0 962598 1.000000 0.287784

Seuraava taulukko näyttää analyysini Quick Cash -pikavoittoominaisuudesta. Oikeassa alakulmassa olevassa solussa näkyy arvo 0,475 dollaria.

Välittömän käteispalautuksen taulukko

Saalis Maksaa Todennäköisyys Palata
6 1 0,012500 0,075000
2 16 0,200000 0,400000
0 63 0,787500 0.000000
Kokonais 80 1.000000 0,475000

Näin ollen ei-progressiivisten voittojen arvo on 0,287784 dollaria + 0,475000 dollaria = 0,762784 dollaria.

Olkoon j yhtä kuin kannattavuusrajan ylittävä jättipotti. Sitten:

2 = 0,762784 + j × (1/962598)
1,237216 = j × (1/962598)
j = 1,237216 × 962598
j = 1 190 941,95 dollaria.

Kokonaistuottoprosentti on 0,381392 plus 0,051943 jokaista jackpotin 100 000 dollaria kohden.

Kuten kysymyksessä todettiin, kaikki tämä jättää huomiotta verot ja jättipottien jakamisen.

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .