WOO logo

Velho suosittelee

Kysy velholta #343

Sivullasi otsikolla "Videopokerin analyysimenetelmäni" todetaan, että videopokerin analysoinnissa on vain 134 459 samanlaista kättä, kun mahdollisia viiden kortin käsiä on 2 598 960.

Tuo on yhden pakan peliä varten. Olen kuullut videopokeripelistä nimeltä Aces Live, jossa käytetään kuutta pakkaa. Kuinka monta viiden kortin käsiluokkaa on olemassa kuudella pakalla?

robomb162

En usein tarvitse apua uhkapelikysymyksessä, mutta Gary Kohler ystävällisesti teki kovan työn vastatakseen tähän kysymykseen. Seuraava taulukko näyttää Garyn käsiluokkien lukumäärän yhdestä kuuteen pakalla.

Videopokerin käsiluokat

Kannet Kokonais
Yhdistelmät		 Kokonais
Käsien tunnit
1 2 598 960 134 459
2 91 962 520 202 735
3 721 656 936 208 143
4 3 091 033 296 208 468
5 9 525 431 552 208 481
6 23 856 384 552 208 481

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Mikä on todennäköisyys sille, että baccaratissa on neloset, viitoset ja kuutoset, kun kaikki pelaajan ja pankkiirin käden kesken jaetut kortit lasketaan yhteen kaikilla 13 arvoasteikolla?

anonyymi

Seuraava taulukko näyttää kaikkien neljen, viitosten ja kuutosten permutaatioiden määrän baccaratissa arvojärjestyksessä 4 998 398 275 503 360 mahdollisesta permutaatiosta.

Kenon 4-6-permutaatiot baccaratissa

Sijoitus Neloset Viisi samanlaista Kuusi samanlaista
Ässä 1 174 231 511 040 40 210 759 680 652 458 240
2 1 130 651 443 200 36 344 340 480 652 458 240
3 840 162 535 680 - -
4 431 482 026 240 - -
5 1 201 241 210 880 43 303 895 040 652 458 240
6 1 079 228 067 840 40 210 759 680 652 458 240
7 986 765 414 400 30 158 069 760 652 458 240
8 502 955 546 880 - -
9 230 538 696 960 - -
10 1 174 176 276 480 40 210 759 680 652 458 240
Jack 1 174 176 276 480 40 210 759 680 652 458 240
kuningatar 1 174 176 276 480 40 210 759 680 652 458 240
Kuningas 1 174 176 276 480 40 210 759 680 652 458 240
Kokonais 12 273 961 559 040 351 070 863 360 5 872 124 160

Seuraava taulukko näyttää kaikkien nelos-, viitos- ja kuutosarvoisten korttien todennäköisyyden baccaratissa arvojärjestyksessä.

Kenon 4-6-todennäköisyydet baccaratissa

Sijoitus Neloset Viisi samanlaista Kuusi samanlaista
Ässä 0.0002349216 0.0000080447 0.0000001305
2 0.0002262028 0.0000072712 0.0000001305
3 0.0001680864 0.0000000000 0.0000000000
4 0.0000863241 0.0000000000 0.0000000000
5 0.0002403252 0.0000086636 0.0000001305
6 0.0002159148 0.0000080447 0.0000001305
7 0.0001974163 0.0000060335 0.0000001305
8 0.0001006233 0.0000000000 0.0000000000
9 0.0000461225 0.0000000000 0.0000000000
10 0.0002349105 0.0000080447 0.0000001305
Jack 0.0002349105 0.0000080447 0.0000001305
kuningatar 0.0002349105 0.0000080447 0.0000001305
Kuningas 0.0002349105 0.0000080447 0.0000001305
Kokonais 0,0024555789 0.0000702367 0.0000011748

Kuutio on kolmiulotteinen kappale, joka koostuu yksikköneliöistä.

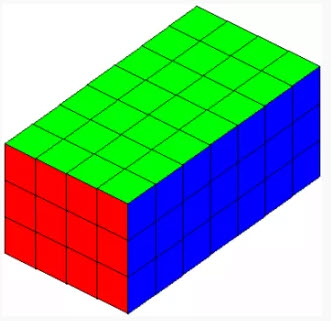
kuutiomainen

Särmiö a × b × c muodostetaan abc identtisestä yksikkökuutiosta, kuten 3x3x3 Rubikin kuutio. Jaa kuutiot kahteen toisensa poissulkevaan tyyppiin. Ulkoiset kuutiot muodostavat särmiön sivut; sisäkuutiot ovat täysin suljettuja. Esimerkiksi kuvassa olevassa särmiössä on 74 ulkoista ja 10 sisäistä kuutiota.

Anna kaikkien sellaisten suorakulmaisten särmiöiden mitat, joilla on ulkoisten kuutioiden lukumäärä yhtä suuri kuin sisäisten kuutioiden lukumäärä.

Gialmere

Tällaisia särmiöitä on 20 mahdollista.
[spoiler=Tarkat mitat]
  1. 5 × 13 × 132
  2. 5 x 14 x 72
  3. 5 x 15 x 52
  4. 5 x 16 x 42
  5. 5 x 17 x 36
  6. 5 x 18 x 32
  7. 5 x 20 x 27
  8. 5 x 22 x 24
  9. 6 x 9 x 56
  10. 6 x 10 x 32
  11. 6 x 11 x 24
  12. 6 x 12 x 20
  13. 6 x 14 x 16
  14. 7 x 7 x 100
  15. 7 x 8 x 30
  16. 7 x 9 x 20
  17. 7 x 10 x 16
  18. 8 x 8 x 18
  19. 8 x 9 x 14
  20. 8 x 10 x 12
[/spoileri]

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .