Kysy velholta #352
Kuinka paljon maksimivoitot lisäävät talon etua Mississippi Studissa?
Hyvä kysymys. Mississippi Stud -pelaajien tulisi ehdottomasti olla tietoisia siitä, että maksimivoitot voivat pienentää heidän voittojaan kuningasvärisuorassa, mikä puolestaan lisää talon etua.
Mississippi Studissa suurin voitto on 500:1 kuningasvärisuoralle, ja tämä koskee kaikkia panoksia. Pelaajalla on kaksi mahdollisuutta korottaa panostaan jopa kolminkertaiseksi alkupanoksensa verran, joten hänen lopullinen panoksensa voi olla jopa seitsenkertainen alkupanoksensa verran. Jos pelaajalla on toivoa kuningasvärisuorasta, hänen tulisi maksimoida enimmäiskorotukset.
Mississippi Studissa pelaajan tulisi panostaa alkupanokseen enintään 22,86 dollaria ilman, että voittokatto vaikuttaa peliin.
Seuraava taulukko näyttää talon edun eri panostuksilla ja yleisillä maksimivoitoilla. Taulukko olettaa optimaalisen pelaajastrategian ilman voittokattoa. Huomaa, kuinka talon etu kasvaa panoksen koon kasvaessa ja voittokaton pienentyessä.
Talon etu ja voittokatto
| Veto | 50 000 dollarin yläraja | 80 000 dollarin yläraja | 100 000 dollarin yläraja |
|---|---|---|---|
| 15 dollaria | 5,02 % | 4,91 % | 4,91 % |
| 20 dollaria | 5,15 % | 4,91 % | 4,91 % |
| 25 dollaria | 5,22 % | 5,04 % | 4,91 % |
| 50 dollaria | 5,38 % | 5,28 % | 5,22 % |
| 75 dollaria | 5,49 % | 5,37 % | 5,33 % |
| 100 dollaria | 5,64 % | 5,41 % | 5,38 % |
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Vital Vegas on ottanut pelaajan moitteeseen, koska tämä antoi vain 200 dollaria tippiä 1,1 miljoonan dollarin jättipotista. Mikä on sopiva etiketti tippaamiseen tällaisessa tilanteessa?
Kyllä, vaikka he nuhtelevat pelaajaa pienestä tippistä, he kätevästi väistelevät kysymystä siitä, mikä on sopiva tippi.
Tipin antamisetiketti ei ole hyvin määritelty vain suurissa jättipoteissa, eikä edes pienissä. Mielipiteet vaihtelevat laidasta laitaan, ja monet niistä ovat ihmisten esittämiä, jotka eivät ole koskaan voittaneet jättipottia.
Ensinnäkin haluan korostaa, että tippaaminen ei ole valinnaista. Kasinolla odotetaan tippaa saamastasi palvelusta, voitetun summan ja palvelutason mukaan. Tässä vaiheessa on helppo muuttua herra Pinkiksi ja järkeillä, miksi heidän ei pitäisi antaa tippiä mistään. Tipin antaminen on ehdottomasti virheellinen järjestelmä, mutta se on järjestelmä, joka meillä on. Jos et ole samaa mieltä ja kieltäydy antamasta tippiä, älä pyydä mistään palvelusta, josta tippiä odotetaan.
Toiseksi, kun asia on sovittu, pelaajan tulisi antaa tippiä jackpotista, kuinka paljon? Rajoitan tätä keskustelua tilanteisiin, joissa pelaaja voittaa vain yhden jackpotin. Säännöt ovat erilaiset, jos pelaaja voittaa useita jackpoteja, mikä on normaalia erittäin korkeilla panostasoilla. Muista, että jackpot-paperien läpikäymistä koskevat säännöt ovat:
- Voita 1 200 dollaria tai enemmän "kolikkopeleissä".
- Voita kenossa 1 500 dollaria tai enemmän.
- Voita 5 000 dollaria tai enemmän pokeriturnauksessa.
- Voita pöytäpeleissä vähintään 600 dollaria JA vähintään 300-kertainen panos.
Mitä suosittelen tippaamaan? Aiemmin olen sanonut, että 0,5–2 % jättipotista, mitä suurempi jättipotti, sitä pienempi prosenttiosuus. En kuitenkaan ajatellut tuolloin näin suuria jättipotteja. Mielestäni tuo vaihteluväli on sopiva noin 100 000 dollariin asti.
Tämä kysymys on saanut minut luomaan erityisen kaavan, jonka mielestäni sopii mille tahansa jättipotille 1 200 dollarista miljooniin. Tässä se on:
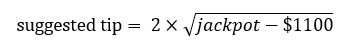
Jos et näe kuvaa, se on 2 × neliöjalkaa (pääpotti - 1100 dollaria).
Tässä on kaava, joka antaa joillekin yleisille jättipottimäärille.
Ehdotettu vinkkitaulukko
| Jättipotti | Kärki |
|---|---|
| 1 200 dollaria | 20 dollaria |
| 2 000 dollaria | 60 dollaria |
| 5 000 dollaria | 125 dollaria |
| 10 000 dollaria | 189 dollaria |
| 20 000 dollaria | 275 dollaria |
| 50 000 dollaria | 442 dollaria |
| 100 000 dollaria | 629 dollaria |
| 1 000 000 dollaria | 1 999 dollaria |
1,1 miljoonan dollarin tapauksessa kaavani ehdottaa 2 096,57 dollaria. Mielestäni on ihan ok pyöristää alaspäin 2 000 dollariin. Tietenkin on otettava huomioon myös muut tekijät, kuten palvelun laatu.
Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .
Mikä on minkä tahansa suuren luvun lähellä olevien alkulukujen keskimääräinen etäisyys? Kuinka monta alkulukua on tätä lukua pienempiä?
Erittäin hyvä arvio alkulukujen välisen keskimääräisen etäisyyden kuvaamiseksi lähellä mitä tahansa suurta lukua n on ln(n). On huomionarvoista, kuinka hyvä tämä estimaattori on.
Todisteena seuraava taulukko esittää ensimmäisten 15 miljoonan alkuluvun vaihteluvälin miljoonan kappaleen ryhmissä. Taulukko näyttää alkulukujen välisen keskimääräisen etäisyyden vaihteluvälillä ja keskimääräisen etäisyyden arvion. Arvio on vaihteluvälin suurimman ja pienimmän alkuluvun keskiarvon luonnollinen logaritmi. Esimerkiksi miljoonan alkuluvun 15. ryhmälle se on ln((256 203 221 + 275 604 541) / 2).
Alkulukujen keskimääräinen etäisyys
| Ensimmäinen pääministeri alueella | Viimeinen alku alueella | Alkulukuja alueella | Keskimääräinen etäisyys | Arvio | |
|---|---|---|---|---|---|
| 2 | 15 485 863 | 1 000 000 | 15.485861 | 15.86229105 | |
| 15 485 867 | 32 452 843 | 1 000 000 | 16.966976 | 16.9922867 | |
| 32 452 867 | 49 979 687 | 1 000 000 | 17.52682 | 17.53434381 | |
| 49 979 693 | 67 867 967 | 1 000 000 | 17.888274 | 17.89175615 | |
| 67 867 979 | 86 028 121 | 1 000 000 | 18.160142 | 18.15864108 | |
| 86 028 157 | 104 395 301 | 1 000 000 | 18.367144 | 18.3716137 | |
| 104 395 303 | 122 949 823 | 1 000 000 | 18.55452 | 18.54883262 | |
| 122 949 829 | 141 650 939 | 1 000 000 | 18.70111 | 18.70058553 | |
| 141 650 963 | 160 481 183 | 1 000 000 | 18.83022 | 18.83322787 | |
| 160 481 219 | 179 424 673 | 1 000 000 | 18.943454 | 18.95103217 | |
| 179 424 691 | 198 491 317 | 1 000 000 | 19.066626 | 19.05703535 | |
| 198 491 329 | 217 645 177 | 1 000 000 | 19.153848 | 19.15337672 | |
| 217 645 199 | 236 887 691 | 1 000 000 | 19.242492 | 19.24163365 | |
| 236 887 699 | 256 203 161 | 1 000 000 | 19.315462 | 19.32305683 | |
| 256 203 221 | 275 604 541 | 1 000 000 | 19.40132 | 19.39864545 |
Lähde: Primeiden väliset aukot Prime Pagesissa.
Saadaksemme minkä tahansa luvun alle olevien alkulukujen lukumäärän, voimme aloittaa integroimalla ln(n):n keskimääräisen etäisyyden estimaatin. Tämä antaa meille alkulukujen välisten keskimääräisten etäisyyksien summan mihin tahansa lukuun n asti.
Mikä on funktion f(n)=ln(n) integraali? Muista, että osittaisella integroinnilla saadaan seuraava kuvaus:
Funktion f(n)*g'(n) integraali dn = f(n)*g(n) - funktion (f'(n)*g(n)) integraali dn
Olkoon f(n)=ln(n) ja g'(n)=1. Tällöin f'(n)=1/n ja g(n)=n. ln(n):n integraali on siis ln(n)*n - ((1/n)*n):n integraali = ln(n)*n - n = n*(ln(n)-1)
Jos jaamme n*(ln(n)-1) luvulla n, saamme alkulukujen keskimääräisen etäisyyden lukuvälillä 2-n. Tämä on ln(n)-1.
Jos jaamme n tällä alkulukujen keskimääräisellä etäisyydellä, saamme alkulukujen keskimääräisen lukumäärän, jonka etäisyydellä n on n, eli n/(ln(n)-1).
Todisteena seuraava taulukko näyttää alkulukujen lukumäärän eri suurilla luvuilla ja niiden arvioidun arvon. Pahoittelen 15 merkitsevän numeron tarkkuutta, joka on kaikki mitä Excel sallii. Joku voisi tehdä laskentataulukon, joka pystyy käsittelemään enemmän.
Alkulukujen keskimääräinen etäisyys
| n | Alkulukujen n alainen | n/(ln(n)-1) |
|---|---|---|
| 10 | 4 | 8 |
| 100 | 25 | 28 |
| 1 000 | 168 | 169 |
| 10 000 | 1 229 | 1 218 |
| 100 000 | 9 592 | 9 512 |
| 1 000 000 | 78 498 | 78 030 |
| 10 000 000 | 664 579 | 661 459 |
| 100 000 000 | 5 761 455 | 5 740 304 |
| 1 000 000 000 | 50 847 534 | 50 701 542 |
| 10 000 000 000 | 455 052 511 | 454 011 971 |
| 100 000 000 000 | 4 118 054 813 | 4 110 416 301 |
| 1 000 000 000 000 | 37 607 912 018 | 37 550 193 650 |
| 10 000 000 000 000 | 346 065 536 839 | 345 618 860 221 |
| 100 000 000 000 000 | 3 204 941 750 802 | 3 201 414 635 781 |
| 1 000 000 000 000 000 | 29 844 570 422 669 | 29 816 233 849 001 |
| 10 000 000 000 000 000 | 279 238 341 033 925 | 279 007 258 230 820 |
| 100 000 000 000 000 000 000 | 2 623 557 157 654 230 | 2 621 647 966 812 030 |
| 1 000 000 000 000 000 000 | 24 739 954 287 740 800 | 24 723 998 785 920 000 |
| 10 000 000 000 000 000 000 000 | 234 057 667 276 344 000 | 233 922 961 602 470 000 |
| 100 000 000 000 000 000 000 000 | 2 220 819 602 560 910 000 | 2 219 671 974 013 730 000 |
| 1 000 000 000 000 000 000 000 | 21 127 269 486 018 700 000 | 21 117 412 262 910 000 000 |
| 10 000 000 000 000 000 000 000 000 | 201 467 286 689 315 000 000 | 201 381 995 844 660 000 000 |
| 100 000 000 000 000 000 000 000 000 | 1 925 320 391 606 800 000 000 | 1 924 577 459 166 810 000 000 |
| 1 000 000 000 000 000 000 000 000 000 | 18 435 599 767 349 200 000 000 | 18 429 088 896 563 900 000 000 |
| 10 000 000 000 000 000 000 000 000 000 | 176 846 309 399 143 000 000 000 | 176 788 931 049 964 000 000 000 |
Lähde: Kuinka monta Primet ovat olemassa? osoitteessa Prime Pages.


