Kysy velholta #353
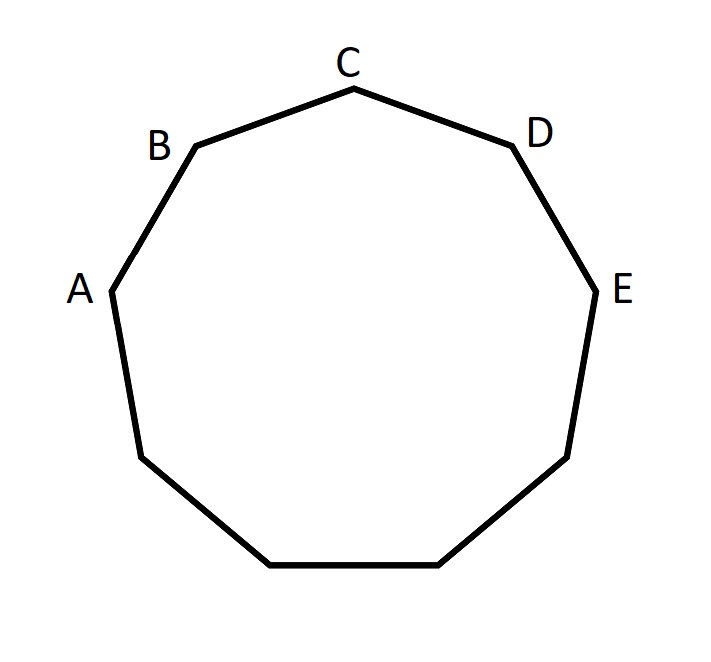
Yllä oleva kuva on yhdeksänkulmio, jonka sivun pituus on yksi.
Kumpi on enemmän, AB+AC vai AE?
Tämä ongelma on otettu Mensa Bulletinin maaliskuun 2021 numerosta.
Tässä on ratkaisuni tähän ongelmaan. (PDF)
Miten voin helposti löytää minkä tahansa kolmi- tai nelinumeroisen luvun neliöjuuren olettaen, että vastaus on kokonaisluku?
Seuraavassa taulukossa näkyvät numerot 0–9, kunkin neliön ja kyseisen neliön viimeisen numeron.
Neliölukujen viimeinen numero
| Alkuperäinen Määrä | Neliö | Viimeinen numero neliöstä |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 4 | 4 |
| 3 | 9 | 9 |
| 4 | 16 | 6 |
| 5 | 25 | 5 |
| 6 | 36 | 6 |
| 7 | 49 | 9 |
| 8 | 64 | 4 |
| 9 | 81 | 1 |
Huomaa, että parilliset neliöluvut päättyvät aina lukuun 0, 1, 4, 5, 6 tai 9. Tämä pätee kaikkiin neliöihin. Tämä johtuu siitä, että alkuperäisen luvun viimeinen numero määrää neliön viimeisen numeron.
Vaihe 1: Neliön viimeisen numeron perusteella voimme käyttää seuraavaa taulukkoa neliöjuuren viimeisen numeron rajaamiseen. Esimerkiksi jos 2809 on neliö, niin neliöjuuren viimeinen numero on 3 tai 7.
Alkuperäisen numeron viimeinen numero
| Viimeinen numero neliöjuuresta | Viimeinen numero neliöstä |
|---|---|
| 0 | 0 |
| 1 | 1 tai 9 |
| 4 | 2 tai 8 |
| 5 | 5 |
| 6 | 4 tai 6 |
| 9 | 3 tai 7 |
Vaihe 2: Seuraavaksi ota alkuperäinen luku ja poista siitä kaksi oikeanpuoleista numeroa. Esimerkiksi, jos alkuperäinen luku oli 2809, käytä lukua 28.
Vaihe 3: Etsi pienin neliöluku, joka on pienempi tai yhtä suuri kuin vaiheen 2 tulos. Ota sitten kyseisen neliöluvun neliöjuuri. Esimerkiksi pienin neliö, joka on pienempi kuin 28, on 25. Ota luvun 25 neliöjuuri, niin saat 5.
Jos et ole muistanut neliöitä sataan asti, voit käyttää seuraavaa taulukkoa.
Neliöjuuren ensimmäinen osa
| Vaihe 2 | Vaihe 3 |
|---|---|
| 1–3 | 1 |
| 4–8 | 2 |
| 9–15 | 3 |
| 16–24 | 4 |
| 25–35 | 5 |
| 36–48 | 6 |
| 49–63 | 7 |
| 64–80 | 8 |
| 81–99 | 9 |
Vaihe 4: Jos vaiheen 1 tulos on 0 tai 5, lisää se vaiheen 3 tuloksen jälkeen ja olet valmis.
Muussa tapauksessa olkoon a = vaiheen 3 tulos. Olkoon b = a×(a+1). Esimerkiksi, jos vaiheen 3 tulos on 5, niin b = 5×6 = 30.
Vaihe 5: Jos b < a, neliöjuuren viimeinen numero on vaiheen 1 mahdollisuuksista pienempi. Muussa tapauksessa, jos b > = a, se on kahdesta mahdollisuudesta suurempi.
Vaihe 6: Saat neliöjuuren ottamalla vaiheen 3 tuloksen ja sen jälkeen vaiheen 5 tuloksen. Toisin sanoen 10 × (vaihe 3) + vaihe 5.
Katsotaanpa joitakin esimerkkejä:
Etsi luvun 256 neliöjuuri.
- Vaihe 1: Neliöjuuren viimeinen numero on 4 tai 6.
- Vaihe 2: Pudottamalla kaksi viimeistä numeroa saadaan 2.
- Vaihe 3: Pienin neliö, joka on pienempi tai yhtä suuri kuin 2, on 1. Luvun 1 neliöjuuri on 1.
- Vaihe 4: 1 * (1 + 1) = 2.
- Vaihe 5: Vaiheen 4 tulos on yhtä suuri kuin vaiheen 2 tulos, joten käytämme viimeisenä numerona vaiheen 1 vaihtoehdoista suurempaa, joka on 6.
- Vaihe 6: Neliöjuuri on luvun 3 tulos, johon on liitetty vaiheen 5 tulos, jolloin saadaan 1 ja 6 = 16.
Etsi luvun 1369 neliöjuuri.
- Vaihe 1: Neliöjuuren viimeinen numero on 3 tai 7.
- Vaihe 2: Jättämällä pois kaksi viimeistä numeroa saamme luvun 13.
- Vaihe 3: Pienin neliö, joka on pienempi tai yhtä suuri kuin 13, on 9. Luvun 9 neliöjuuri on 3.
- Vaihe 4: 3 * (1 + 3) = 12.
- Vaihe 5: Vaiheen 2 tulos on suurempi kuin vaiheen 4 tulos, joten käytämme viimeisenä numerona vaiheen 1 vaihtoehdoista suurempaa, joka on 7.
- Vaihe 6: Neliöjuuri on luvun 3 tulos, johon on liitetty vaiheen 5 tulos, jolloin saadaan 3 ja 7 = 37.
Laske luvun 2704 neliöjuuri.
- Vaihe 1: Neliöjuuren viimeinen numero on 2 tai 8.
- Vaihe 2: Jättämällä pois kaksi viimeistä numeroa saamme luvun 27.
- Vaihe 3: Pienin neliö, joka on pienempi tai yhtä suuri kuin 27, on 25. Luvun 25 neliöjuuri on 5.
- Vaihe 4: 5 * (1 + 5) = 60.
- Vaihe 5: Vaiheen 2 tulos on pienempi kuin vaiheen 4 tulos, joten käytämme vaiheen 1 vaihtoehdoista pienempää viimeisenä numerona, joka on 2.
- Vaihe 6: Neliöjuuri on luvun 3 tulos, johon on liitetty vaiheen 5 tulos, jolloin saadaan 5 ja 2 = 52.
Laske luvun 5625 neliöjuuri.
- Vaihe 1: Neliöjuuren viimeinen numero on 5.
- Vaihe 2: Jättämällä pois kaksi viimeistä numeroa saamme luvun 56.
- Vaihe 3: Pienin neliö, joka on pienempi tai yhtä suuri kuin 56, on 49. Luvun 49 neliöjuuri on 7.
- Vaihe 4: Vaiheen 1 tulos on 0 tai 5, joten vastaus on vaiheen 3 tulos lisättynä vaiheen 1 tuloksella: 7 ja 5 = 75
Laske luvun 6561 neliöjuuri.
- Vaihe 1: Viimeinen numero on 1 tai 9.
- Vaihe 2: Jättämällä pois kaksi viimeistä numeroa saamme luvun 65.
- Vaihe 3: Pienin neliö, joka on pienempi tai yhtä suuri kuin 65, on 64. Luvun 64 neliöjuuri on 8.
- Vaihe 4: 8 * (1 + 8) = 72.
- Vaihe 5: Vaiheen 2 tulos on pienempi kuin vaiheen 4 tulos, joten käytämme vaiheen 1 vaihtoehdoista pienempää viimeisenä numerona, joka on 1.
- Vaihe 6: Neliöjuuri on luvun 3 tulos, johon on liitetty vaiheen 5 tulos, jolloin saadaan 8 ja 1 = 81.
Voit katsoa tämän menetelmän esittelyn YouTubesta .
Mikä on todennäköisyys saada 60 tai enemmän peräkkäistä voittoa 12 tunnin blackjackin pelaamisen aikana?
Blackjackin varianssisivuni mukaan, liberaalien Strip-sääntöjen perusteella, nettovoiton, -tasapelin tai -häviön todennäköisyydet ovat seuraavat:
- Voitto — 42,43 %
- Työntö — 8,48 %
- Tappio — 49,09 %
Jätetään tasapelit huomiotta, jolloin voittotodennäköisyydeksi saadaan 46,36 %, olettaen, että käsi päättyy voittoon tai tappioon.
Käytetään pelinopeudena 100 kättä tunnissa.
Voimme arvioida todennäköisyyden nähdä ainakin yksi vähintään 60 käden putki peräkkäin seuraavasti:
100 × 12 × 0,4636 60 = 1 luvusta 89 412 355 233 588 500.Vertailukohtana, jos ostit Powerball-arvontan ja yhden Megamillions-lipun, molempien voittotodennäköisyys olisi 1/88 412 922 115 818 300.
Joten olisi hieman todennäköisempää voittaa molemmat lotossa kuin nähdä 60 voittoa peräkkäin 12 tunnin pelin aikana.


