Kysy velholta #355
Elokuvassa Lupa tappaa James Bond pelaa kolme kierrosta blackjackia, viisi kättä kerrallaan. Huomaan, ettei hän koskaan osunut yhteenkään niistä. Mitkä ovat todennäköisyydet?
Löydät kohtauksesta videon YouTubesta .
Peli näkee epäilyttävän paljon isoja kortteja, eikö totta? Tässä ovat kortit, jotka pystyin erottamaan. Huomaa, että joissakin tapauksissa kortteja ei voinut nähdä selvästi.
Lupa tappaa -- Arvot havaittu
| Sijoitus | Havaittu |
|---|---|
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 2 |
| 6 | 2 |
| 7 | 1 |
| 8 | 4 |
| 9 | 4 |
| 10 | 8 |
| J | 3 |
| Q | 6 |
| K | 4 |
| A | 1 |
| Kokonais | 35 |
Olet todellakin oikeassa, Bond ei osu yhteenkään 15 alkuperäisestä kädestään. Hän jakaa kasit kerran, mutta ei osu jaon jälkeenkään. Tässä on hänen alkuperäisten toimiensa määrä kaikilla 15 kädellä:
- Tupla — 1
- Jaettu — 1
- Jalusta — 13
Tässä ovat kunkin alkutoiminnon perusstrategiatodennäköisyydet olettaen kuusi pakkaa, tuplaus jaon jälkeen sallittu, jakaja kurkistaa taskukorttiinsa ja jakaja jää pehmeän 17:n päälle.
Blackjack -- Ensimmäisen toiminnan todennäköisyydet
| Toiminta | Todennäköisyys |
|---|---|
| Jalusta | 43,46 % |
| Osuma | 39,78 % |
| Kaksinkertainen | 9,53 % |
| Jakaa | 2,48 % |
| Blackjack | 4,75 % |
| Kokonais | 100,00 % |
Jos antautuminen sallittaisiin, todennäköisyys olisi 4,14 % ja se laskettaisiin pystyssä pysymisen todennäköisyydestä.
On huomattava, että Bond kerran jäi käteen 16 vastaan 10. Perusstrategiana on saada se, mutta se on hyvin marginaalinen. Ottaen huomioon tuossa kädessä tulvan kymppejä, Bond on saattanut tietää, että lasku oli korkea, mikä laukaisi perusstrategiapoikkeuksen jäädessään kyseisessä tilanteessa.
Todennäköisyys sille, ettei yhtäkään kättä osu, on 60,22 %. Todennäköisyys sille, ettei 15 kättä 15:stä osu, on 0,602162 15 = 0,000496253 = noin 1 vuonna 2015.
Kalmaripelissä 16 pelaajaa pelaa lasisillalla. Silta on jaettu 18 lasipariin. Jokaisessa lasiparissa yksi lasi on karkaistua ja kestää pelaajan painon. Toinen lasiparin osa on tavallista lasia ja särkyy pelaajan painon alla. Jos pelaaja astuu tavallisen lasinpalan päälle, hän särkee sen ja kaatuu kuolemaansa.
Pelaajien täytyy edetä yksi kerrallaan ennalta määrätyssä järjestyksessä.
Olettaen, että jokaisen lasiaskelman kohdalla arvataan satunnaisesti, mikä on odotettu pelaajien määrä, jotka ylittävät portaat turvallisesti?
Laitan vastauksen ja ratkaisun spoileri-tageihin, jotta maailma voi itse päättää vastauksen.
Todennäköisyys sille, että pelaaja 1 ylittää kentän turvallisesti, on (1/2)^18 = 1/262144 = noin 0,000004.
Pelaajalla 2 on kaksi tapaa ylittää raja turvallisesti:
- Pelaaja 1 ylittää kentän turvallisesti. Tässä tapauksessa pelaaja 2 voi vain kopioida askeleensa.
- Pelaajien 1 ja 2 välillä on vain yksi huono askel. Tämä voi olla 18 mahdollista lasiparia. Todennäköisyys sille, että askeleita on 17 ja yksi huono, on 18*(1/2)^2 = 18/262144 = 0,000069.
Joten todennäköisyys sille, että pelaaja 2 ylittää kentän turvallisesti, on 0,000004 + 0,000069 = 0,000072.
Pelaaja 3 voi ylittää kentän turvallisesti kahdella tavalla:
- Pelaaja 2 ylittää kentän turvallisesti. Tässä tapauksessa pelaaja 3 voi vain kopioida askeleensa.
- Pelaajien 1, 2 ja 3 välillä on vain kaksi huonoa askelta. On combin(18,2)=153 tapaa valita kaksi 18 lasiparista niille kahdelle palalle, jotka tappavat pelaajat 1 ja 2. Todennäköisyys sille, että askeleita on 16 hyvää ja kaksi huonoa, on 153*(1/2)^2 = 153/262144 = 0.000584.
Joten todennäköisyys sille, että pelaaja 3 ylittää kentän turvallisesti, on 0,000072 + 0,000584 = 0,000656.
Pelaajalla 4 on kaksi tapaa ylittää kenttä turvallisesti:
- Pelaaja 3 ylittää pallon turvallisesti. Tässä tapauksessa pelaaja 4 voi vain kopioida askeleensa.
- Pelaajien 1–4 välillä on vain kolme huonoa askelta. On combin(18,3)=816 tapaa valita 3 lasiparia 18:sta kahdelle lasinpalaselle, jotka tappavat pelaajat 1–3. Todennäköisyys sille, että askeleita on 15 ja huonoja kolme, on 816*(1/2)^2 = 816/262144 = 0,003113.
Tätä logiikkaa jatkamalla saamme seuraavan taulukon kunkin pelaajan todennäköisyyksistä.
Bridge-peli
| Pelaaja | Todennäköisyys Selviytyminen |
|---|---|
| 1 | 0.000004 |
| 2 | 0,000072 |
| 3 | 0,000656 |
| 4 | 0,003769 |
| 5 | 0,015442 |
| 6 | 0,048126 |
| 7 | 0.118942 |
| 8 | 0.240341 |
| 9 | 0,407265 |
| 10 | 0,592735 |
| 11 | 0,759659 |
| 12 | 0.881058 |
| 13 | 0,951874 |
| 14 | 0,984558 |
| 15 | 0,996231 |
| 16 | 0.999344 |
| Kokonais | 7.000076 |
Vastauksen ilmaisemiseksi suljetussa muodossa se on:
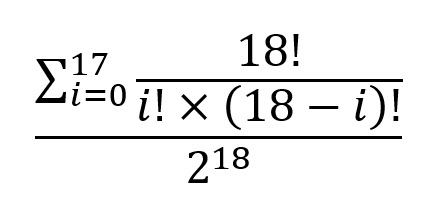
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Ultimate X Gold -pelissäsi sinulle jaetaan ajassa 3:10 täyskäsi, jossa on kolmosia nelosia vastaan. Kerroin nelosille kakkosten ja nelosten välissä oli 9x. Täyskäden kerroin oli 1x. Miksi pidit täyskäden etkä vain kolme kolmosta ja yritit nelosia isolla kertoimella?
Olet oikeassa, mokasin täysin sillä kädellä.
Muistathan, että pelasin 10 pelin pokeria. Näin ollen voittoni täyskädellä oli 10 × 35 = 350.
Vain kolmosia pitäen kummallakin kädellä oli seuraavat todennäköisyydet:
- Neloset — 4,26 %
- Täysi talo — 6,11 %
- Kolmoset — 89,64 %
Tässä ovat voitot kummallekin kädelle kertoimien jälkeen:
- Neloset — 1800
- Täysi talo — 35
- Kolmoset — 15
Odotusarvoinen tuottoni pelkillä kolmosilla olisi ollut (4,26 % * 1800) + (6,11 % * 35) + (89,64 % * 15) = 92,17854. Se on huomattavasti enemmän kuin täyskäden odotettu 35. Joten kyllä, tein kiusallisen virheen tuolla kädellä.
Joku haastoi minut seuraavaan vetoon. Saan valita mitkä tahansa kolme arvoa tavallisesta pokeripakasta ja kirjoittaa ennusteeni muistiin, mutta pitää sen piilossa loppuun asti. Esimerkiksi 7-ässä-2. Sitten hän tarjoutui lyömään vetoa tasarahasta, että osaisi nimetä ainakin yhden arvoistani, jos saisi kolme arvausta. Mitkä olivat voittomahdollisuuteni?
Voittaaksesi vastustajasi on oltava väärässä kaikissa kolmessa ennustuksessa. Ensimmäisellä ennustuksella on 10/13 todennäköisyys olla väärä. Toisella ennustuksella on 9/12 todennäköisyys olla väärä, koska voimme poistaa ensimmäisenä arvatun sijan mahdollisuuksien joukossa. Kolmannella ennustuksella on 8/11 todennäköisyys olla väärä, koska voimme poistaa kaksi ensimmäistä arvattua sijaa mahdollisuuksien joukossa.
Kaikkien näiden kolmen asian pitäisi tapahtua, jotta voitat. Näin ollen voittomahdollisuutesi ovat (10/13) * (9/12) * (8/11) = 720/1716 = 41,96 %.
Tasapelitilanteessa talon etu tässä vedossa on sinun puoleltasi 16,08 % (auts!).
Tämä kysymys on poimittu Owen E'Shean teoksesta The Book of Proposition Bets (numero 7).


