Kysy velholta #367
Tykkään lyödä vetoa kaikista numeroista crapsissa. Kuinka monta ainutlaatuista numeroa voin odottaa saavani ennen kuin saan 7-outin?
Muiden lukijoiden tiedoksi, kysymys kuuluu, kuinka monta seuraavista kokonaisluvuista heitetään kahdella noppaa ennen kuin kokonaisluku on seitsemän: 4, 5, 6, 8, 9 ja 10.
Vastaus on 2,375758. Seuraava taulukko näyttää kunkin yksittäisen mahdollisuuden todennäköisyyden sille, että määritetyllä alueella on nollasta kuuteen ainutlaatuista kokonaissummaa. Oikeassa alakulmassa oleva solu näyttää keskimääräisen yksilöllisen kokonaissumman ennen seitsemän heittämistä.
Yksilölliset heitetyt numerot
| Kokonais | Todennäköisyys | Odotettu |
|---|---|---|
| 6 | 0,062168 | 0.373009 |
| 5 | 0.101016 | 0,505079 |
| 4 | 0.129245 | 0,516979 |
| 3 | 0,151531 | 0,454594 |
| 2 | 0,170057 | 0.340114 |
| 1 | 0,185983 | 0,185983 |
| 0 | 0,200000 | 0.000000 |
| Kokonais | 1.000000 | 2.375758 |
Onko totta, että reilu kolikko osuu todennäköisemmin kuvapuoli ylöspäin sille puolelle, joka alkoi kuvapuoli ylöspäin?
Todisteet viittaavat siihen, että tämä on totta!
Persi Diaconis ja Susan Holmes Stanfordin yliopistosta kirjasivat 10 000 kolikonheittoa. Kolikko laskeutui samalle puolelle ylöspäin kuin se oli alussa 50,8 % ajasta (lähde: The Fifty-one Percent Solution uutiskirjeestä What's Happening in the Mathematical Sciences, jonka on kirjoittanut American Mathematical Society). Todennäköisyys sille, että suhde on niin korkea tai suurempi, on 5,48 %.
Todistaakseni tämän matemaattisesti oletin, että kolikon todellinen kierrosten lukumäärä noudatti Poisson-jakaumaa. Tarkemmin sanottuna, jos kierrosten keskimääräinen lukumäärä oli m, niin täsmälleen n kierroksen todennäköisyys on exp(-m)*m^n/n!. Havainnollistaakseni Poisson-jakaumaa seuraava kaavio näyttää 0–25 kierroksen todennäköisyyden, kun keskiarvo on 10.
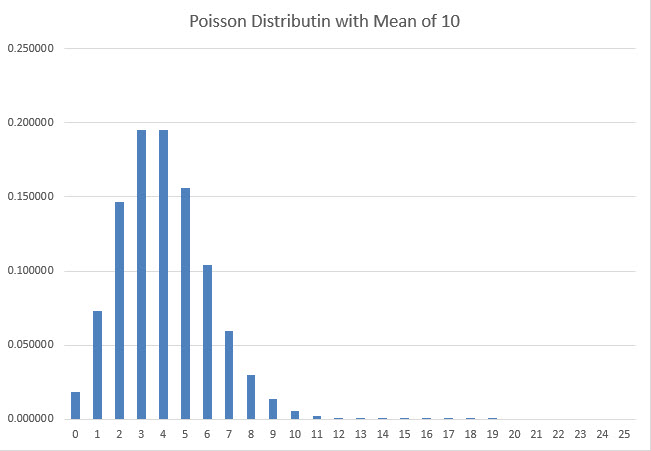
Valitsin Poissonin oletuksen siksi, että se noudattaa lähes kellokäyrän muotoa riittävän suurilla keskiarvoilla, eikä todellinen tulos voi koskaan laskea nollan alapuolelle.
Laskin sitten parillisen määrän puolikierroksia todennäköisyyden (jolloin kone laskeutuu samalle sivulle alaspäin kuin lähtöasennossa) eri puolikierrosten keskiarvoilla. Seuraava taulukko näyttää tulokset 0,5–5,0 keskiarvoilla.
Parillisen ja parittoman kierrosten lukumäärän todennäköisyys
| Keskimääräiset vallankumoukset | Tasapeli yhteensä | Pariton kokonaissumma |
|---|---|---|
| 0,5 | 0.567667642 | 0.432332358 |
| 1 | 0.509157819 | 0.490842181 |
| 1.5 | 0.501239376 | 0.498760624 |
| 2 | 0.500167731 | 0.499832269 |
| 2.5 | 0.500022700 | 0.499977300 |
| 3 | 0.500003072 | 0.499996928 |
| 3.5 | 0.500000416 | 0.499999584 |
| 4 | 0.500000056 | 0.499999944 |
| 4.5 | 0.500000008 | 0.499999992 |
| 5 | 0.500000001 | 0.499999999 |
Sitten aloin miettiä, miksi parillisen luvun todennäköisyys on aina suurempi kuin 50 %. Kävi ilmi, että parillisen luvun todennäköisyys, annettuna m:n keskiarvo, voidaan ilmaista muodossa 0,5 + e^(-2m)/2. e:n potenssiin minkä tahansa on oltava positiivinen, joten myös parillisen kierrosmäärän todennäköisyys on positiivinen.
Voit nähdä todistukseni tälle kaavalle täältä .
Mikä on analyysisi Spelling Bee -pelistä Price is Right -sivustolla?
Muiden lukijoiden tiedoksi, käyn ensin läpi säännöt.
- Pelilaudalla on 30 korttia, jotka on numeroitu 1-30.
- Kunkin kortin kääntöpuolella on kirjain tai sana "auto". Kortit jakautuvat seuraavasti:
- C: 11
- V: 11
- R: 6
- Auto: 2
- Isännät antavat pelaajan valita kaksi korttia.
- Hinnoittelupelin jälkeen, johon en mene tässä tarkemmin, pelaajalla on mahdollisuus ansaita jopa kolme korttia lisää.
- Kortit käännetään ympäri.
- Pelaaja voi voittaa auton kahdella tavalla:
- Pelaaja saa vähintään yhden kortin jokaista kirjainta (jolloin muodostuu sana CAR).
- Pelaaja saa ainakin yhden "AUTO"-korteista.
- Pelaaja voi milloin tahansa pelin aikana antautua ja saada 1 000 dollaria jokaisesta kääntämättä jätetystä kortistaan.
Tässä on klippi pelistä, jota pelataan.
Seuraava taulukko näyttää voittotodennäköisyyden pelaajan korttien lukumäärän mukaan, olettaen, että yhtäkään ei ole vielä käännetty.
Spelling Bee - Voiton Todennäköisyys
| Kortit | Todennäköisyys Voittaminen |
|---|---|
| 2 | 0.131034 |
| 3 | 0,371921 |
| 4 | 0.584018 |
| 5 | 0,734888 |
Ennen kuin yhtään korttia on käännetty, pelaajan ei tule antautua, olettaen että autolla on jokin kohtuullinen arvo. Esimerkiksi, vaikka pelaajalla olisi vain kaksi korttia, hänellä on 13,1 %:n mahdollisuus saada ainakin yksi AUTO-korteista. Pelaajan tulisi suhtautua välinpitämättömästi 2 000 dollarin luovutusarvoon, jos auton arvo olisi 15 263,16 dollaria. Mikä tahansa uusi auto on arvokkaampi kuin se.
Seuraavassa on auton arvoon vaikuttavat pisteet sen mukaan, kuinka monta kääntämätöntä korttia pelaajalla on.
Spelling Bee - Voiton Todennäköisyys
| Kortit | Välinpitämättömyys Kohta |
|---|---|
| 2 | 15 263,16 dollaria |
| 3 | 8 066,23 dollaria |
| 4 | 6 849,11 dollaria |
| 5 | 6 803,75 dollaria |


