Kysy velholta #373
Olen varma, että olet Rillit huurussa -elokuvan fani. Yksi suosikkikohtauksistani on Kivi, paperi, sakset ja lisko Spock -peli. Se on kuin viiden symbolin kivi, paperi, sakset -peli, jossa on seuraavat säännöt:
- Paperi peittää kiven
- Kivi murskaa liskon
- Lisko myrkyttää Spockin
- Spock murskaa sakset
- Sakset leikkaavat paperia
- Lisko syö paperia Spock höyrystää kiven
- Sakset katkaisevat liskon pään
- Paperi kumoaa Spockin väitteet
- Kivi murskaa sakset
Kysymykseni kuuluu, voidaanko lisätä symboleja, jotta jokaisella osapuolella on samat mahdollisuudet satunnaista pelaajaa vastaan?
Kyllä, minäkin rakastan tuota kohtausta! Tässä on siitä YouTube-video .
Tarvitset parittoman määrän symboleja. Teoriassa niitä voisi olla parillinen määrä, mutta silloin pitäisi luoda säännöt, joiden mukaan tietyt eri symbolien parit johtaisivat tasapeliin. Ei, haluamme ratkaisevan pelin, jossa ainoat tasapelit ovat, jos molemmat pelaajat pelaavat saman symbolin.
Ratkaisu on erityisen elegantti ja helppo selittää alkuluvulla symboleja. Selitän esimerkkinä seitsemän symbolin avulla. Merkitään symbolit A:sta G:hen ja esitetään ne ympyrällä seuraavassa kaaviossa.
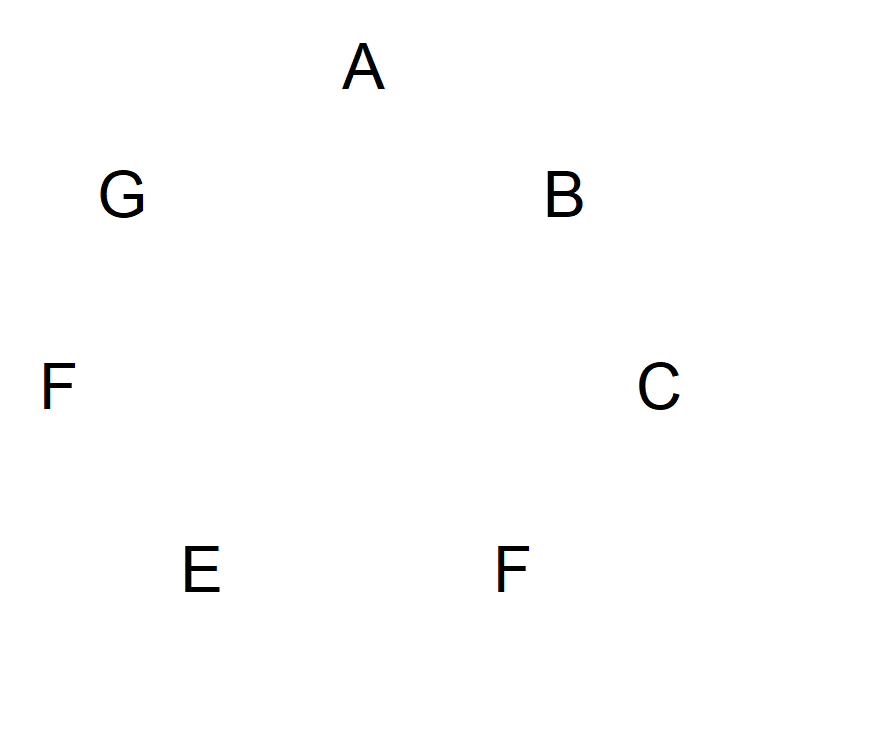
Aloita seuraavaksi kohdasta A ja piirrä sitten nuoli seuraavaan symboliin myötäpäivään. Nuolen tulee osoittaa kohti näiden kahden välistä olevaa kohtaa. Ajattele sitä kuin symbolia ammuttaisiin nuolella. Jatka myötäpäivään, kunnes pääset takaisin kohtaan A. Kaavio ei näytä tältä:
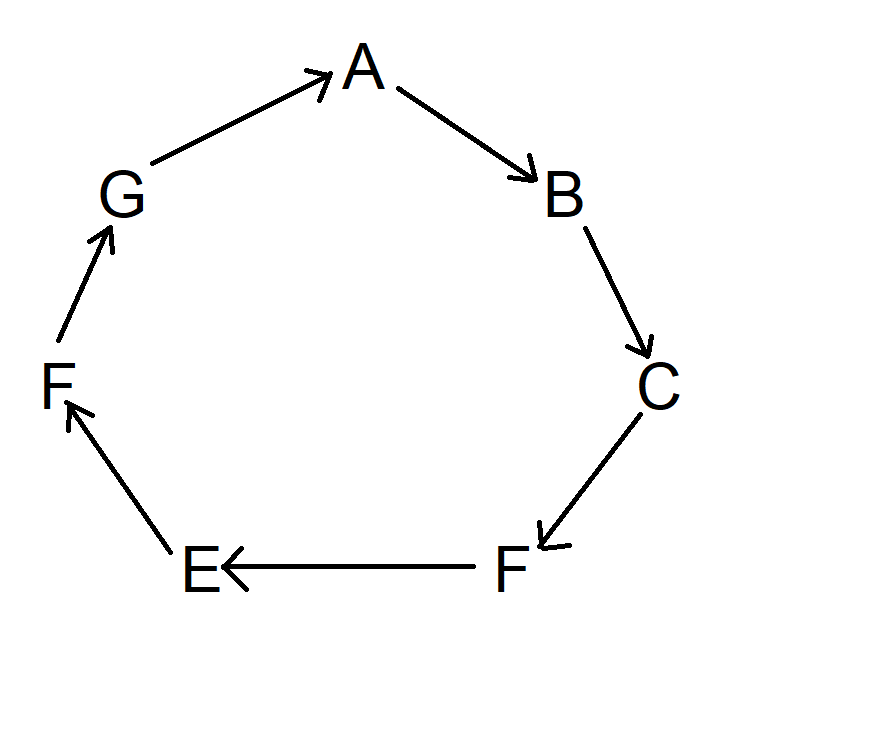
Tee seuraavaksi sama, mutta siirry kaksi symbolia myötäpäivään alkaen A:sta. Itse asiassa voit aloittaa mistä tahansa. Kaavio näyttää nyt tältä:
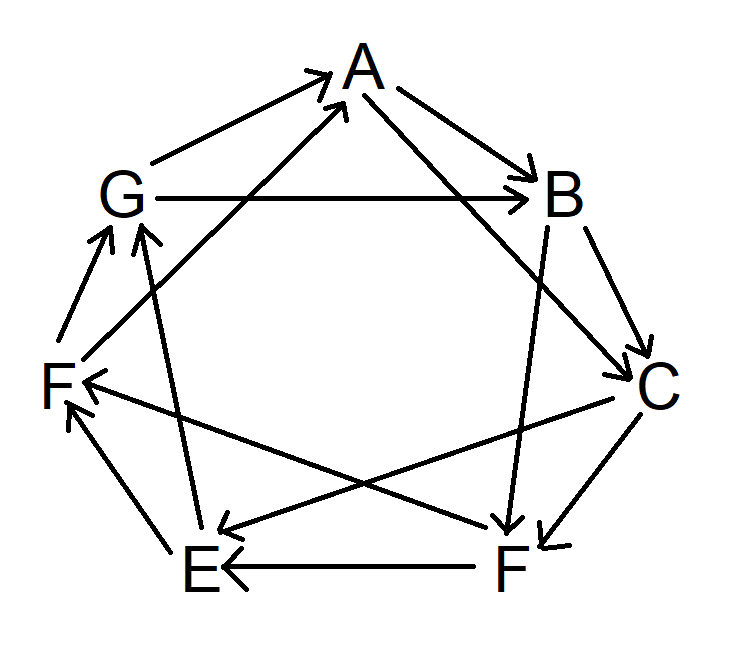
Tee lopuksi sama, mutta jätä kolme symbolia myötäpäivään väliin. Kaavio näyttää nyt tältä:
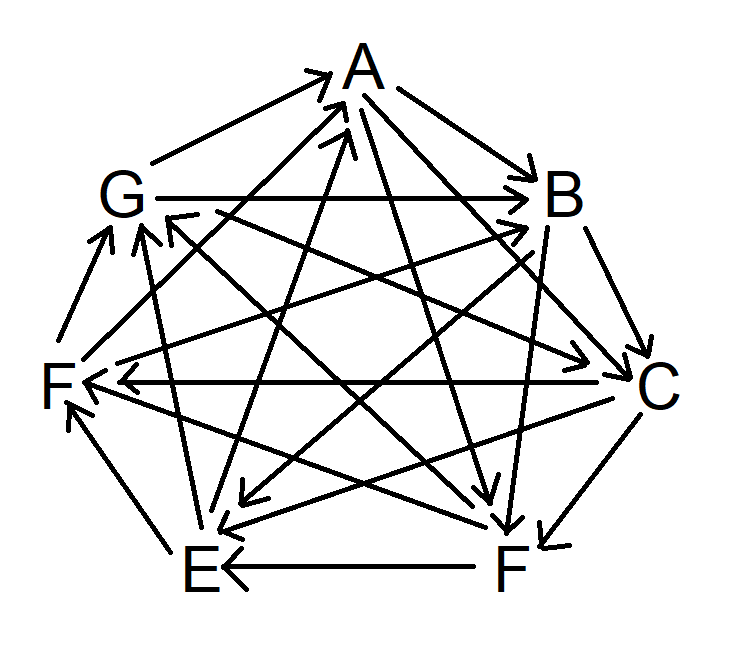
Huomaa tässä vaiheessa jokainen symboli voittaa kolme muuta symbolia ja kolme muuta eri symbolia voittaa sen.
Tämä menetelmä toimii mille tahansa alkuluvulle symboleja, koska kun palaat takaisin alkuperäiseen symboliin, olet käynyt läpi jokaisen symbolin. n symbolin kohdalla sinun on käytävä läpi tämä prosessi (n-1)/2 kertaa.
Voit tehdä tasapainoisen pelin millä tahansa parittolla määrällä symboleja, mutta joskus palaat takaisin alkuperäiseen symboliin liian nopeasti. Kun näin tapahtuu, sinun on tehtävä uusia silmukoita aloittaen niistä symboleista, jotka jäit huomaamatta.
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Mikä on tasapelin todennäköisyys Three Card Pokerissa?
Tarkka vastaus on 450528/407170400 =~ 0,001106485 =~ 1/904.
Seuraava taulukko näyttää, kuinka monta tapaa kutakin aloituskättä voi muodostaa ja kuinka monta korttiyhdistelmää toisessa kädessä tasataan. Suorien ja roskakäsien kohdalla on merkitystä, onko ensimmäisessä kädessä edustettuna kaksi vai kolme maata.
Oikeassa alakulmassa oleva solu näyttää, että Three Card Pokerissa on 450 528 tapaa saada tasapeli. Kahden käden yhdistelmien kokonaismäärä on combin(52,3)*combin(49,3) = 407170400. Näin ollen vastaus on 450528/407170400.
Kolmen kortin pokeritasku
| Käsi | Käsi 1 | Käsi 2 | Tuote |
|---|---|---|---|
| Kolmoset | 52 | 0 | 0 |
| Värisuora | 48 | 3 | 144 |
| Suora (kolme maata) | 288 | 26 | 7 488 |
| Suora (kaksi maata) | 432 | 25 | 10 800 |
| Huuhtele | 1 096 | 3 | 3 288 |
| Pari | 3 744 | 3 | 11 232 |
| Roskaa (kolme maata) | 6 576 | 26 | 170 976 |
| Roskaa (kaksi pukua) | 9 864 | 25 | 246 600 |
| Kokonais | 22 100 | 450 528 |
Mikä on ilmaisen ässäkupongin arvo 6-5 blackjackissa?
Ilmaisen ässän arvosivullani mainitsen sen arvon olevan 50,1844 % panossummasta 3-2 blackjackissa.
Kuuden pakan blackjackissa voittomahdollisuus blackjackin saamiseen, jos ensimmäisenä korttina on ässä, on 29,3139 %. Kun näin tapahtuu, voitat 0,3 yksikköä vähemmän 6-5-blackjackissa kuin 3-2-blackjackissa.
Joten ilmaisen ässän arvo 6-5 kuuden pakan blackjackissa on 50,1844 % × 29,3139 × 0,3 = 41,3902 % alkuperäisestä panoksesta.
Joku haastoi minut lyömään vetoa, että hän pystyisi heittämään kahdella nopalla yhteensä 12 27 heiton aikana. Jos hän ei onnistuisi, voittaisin tasarahat. Koska 12:n heiton todennäköisyys on 1/36, eikö hänen pitäisi heittää keskimäärin 36 kertaa saadakseen 12? Näyttäisi siltä, että kertoimet olisivat minun puolellani, jos vastustajani saisi vain 27 heittoa. Olenko oikeassa, vai missä on laskuvirhe?
Keskimääräinen odotusaika 12:n välillä on todellakin 36 heittoa, mukaan lukien itse 12:n heitto. Se ei kuitenkaan tarkoita, että ne tulevat täsmälleen joka 36. heiton välein. Todennäköisyys sille, ettei heitetä 12:ta, on (35/36). Todennäköisyys sille, ettei sitä tehdä 27 heiton aikana, on (35/36)^27. Joten todennäköisyys sille, että ainakin 12:lla heitetään, on 1-(35/36)^27 = 53,26 %.
Seuraava taulukko näyttää todennäköisyyden saada vähintään luku 12 20–36 heitolla. Huomaa, että tasatilanteessa edun saavuttamiseksi tarvitaan 25 lukua.
Todennäköisyys 12
| Rullat | Todennäköisyys |
|---|---|
| 20 | 43,07 % |
| 21 | 44,66 % |
| 22 | 46,19 % |
| 23 | 47,69 % |
| 24 | 49,14 % |
| 25 | 50,55 % |
| 26 | 51,93 % |
| 27 | 53,26 % |
| 28 | 54,56 % |
| 29 | 55,82 % |
| 30 | 57,05 % |
| 31 | 58,24 % |
| 32 | 59,40 % |
| 33 | 60,53 % |
| 34 | 61,63 % |
| 35 | 62,69 % |
| 36 | 63,73 % |


