Kysy velholta #375
Consumer Reports väittää, että kuluttaja säästää rahaa renkaiden vaihtamisessa. Heidän argumenttinsa on, että etuvetoisissa autoissa, joita useimmat autot ovat, rengas kestää noin 32 000 kilometriä ja takarenkaat noin 96 000 kilometriä. Heidän mukaansa renkaiden paikat voi vaihtaa usein, ja ne kestävät noin 64 000 kilometriä.
Jos yksi kuljettaja ei kuitenkaan vaihta renkaitaan, 120 000 mailin aikana hän voi odottaa käyttävänsä kuusi paria eturenkaita ja kaksi paria takarenkaita, yhteensä 2 × (2 + 6) = 16 rengasta. Samaan aikaan toinen kuljettaja vaihtaa renkaitaan, jolloin hän käyttää kolmet neljän renkaan sarjat, yhteensä 12 rengasta.
Tässä on jotain hämärää. Eikö renkaiden kokonaiskitka ole sama mailia kohden riippumatta siitä, vaihdetaanko niitä vai ei? En kiellä renkaiden vaihtamisen turvallisuushyötyjä, mutta miksi renkaat kuluisivat taianomaisesti hitaammin, jos niitä vaihdetaan?
Hyvä kysymys. Olen samaa mieltä laskelmistasi, jotka perustuvat Consumer Reportsin esittämiin oletuksiin. En kuitenkaan ole samaa mieltä heidän oletuksistaan. Näyttää siltä, että he olivat laiskoja ja ottivat huomioon etu- ja takarenkaiden keskimääräisen käyttöiän määrittäessään pyöritetyn renkaan käyttöikää.
Havainnollistamiseksi ajatellaan kuljettajaa, joka aloittaa neljällä uudella renkaalla. Hän vaihtaa sitten etu- ja takarenkaat 25 000 mailin jälkeen. Ennen vaihtoa eturenkaat olisivat kuluneet 75 % ja takarenkaat 25 %. Vaihdon jälkeen eturenkaiden kulutuspintaa on jäljellä 75 % ja takarenkaiden 25 %. Sitten hän ajaa toiset 25 000 mailia. Jälleen kerran eturenkaat kuluvat 75 % uusiin renkaisiin verrattuna ja takarenkaat 25 %. Näin ollen kummankin kulutuspinta on nolla 30 000 mailin jälkeen. Ei 40 000, kuten Consumer Reports väittää.
Saadaksesi oikean käyttöiän renkaiden vaihtamisen avulla, tulee ottaa kulutuspinnan kulumisen keskiarvo. Tässä tapauksessa keskiarvot ovat 1/20 000 ja 1/60 000, jolloin saadaan 1/30 000. Sitten otetaan tämän keskimääräisen kulumisen käänteisluku mailia kohden, jolloin saadaan renkaiden vaihtamisen käyttöikä, joka on 30 000. Tai voit käyttää kaavaa 2*F*R/(F+R), jossa F = eturenkaan käyttöikä ja R = takarenkaan käyttöikä.
Tätä kysymystä on kysytty ja siitä keskustellaan foorumillani Wizard of Vegasissa .
Tiedämme, että mahdollisia viiden kortin yhdistelmiä 52:sta on combin(52,5)=2 598 960. Kysymykseni kuuluu, kuinka monta mahdollista viiden kortin kättä on mahdollista saada viiden pakan kengästä?
Otetaan tämä yksi käsityyppi kerrallaan.
- Viisi samanlaista korttia: Pakassa on 52 erilaista korttia, jotka muodostavat 52 yhdistelmää.
- Nelonen samasta kortista: Neloselle on 52 mahdollista korttia ja singletonille 51. Neloselle on siis 52 * 51 = 2 652 mahdollista yhdistelmää.
- Kolme samaa korttia ja kaksi toista korttia: Kolmelle samanlaiselle kortille on 52 mahdollista korttia ja parille 51. Täyskädelle on siis 52 * 51 = 2 652 mahdollista yhdistelmää.
- Kolme samanlaista korttia ja kaksi erilaista yksittäiskorttia: Kolmelle samanlaiselle kortit ovat mahdollisia 52 ja kahdelle yksittäiskortille combin(51,2)=1 275. Kolmosille on siis 52 * 1 275 = 66 300 mahdollista yhdistelmää.
- Kaksi paria samoja kortteja ja yksi singleton: Kahden eri kortin parit muodostavat combin(52,2) = 1 326 yhdistelmää. Sitten singletonille jää 50 yhdistelmää. Joten kahdelle parille on 1 326 * 50 = 66 300 mahdollista yhdistelmää.
- Yksi saman kortin pari ja kolme yksittäiskorttia: Parille on 52 mahdollista korttia. Sitten on combin(51,3) = 20 825 tapaa valita 3 korttia jäljellä olevista 51 kortista yksittäiskorteille. Joten parin yhdistelmien lukumäärä on 52 * 20 825 = 1 082 900.
- Viisi yksittäistä korttia: Viisi korttia 52:sta voi valita combin(52,5)=2 598 960 tavalla.
Kaikkien näiden yhdistelmien summa on 3 819 816.
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Tarkastellaan seuraavaa kaaviota, jossa on neliö ja ympyrä?
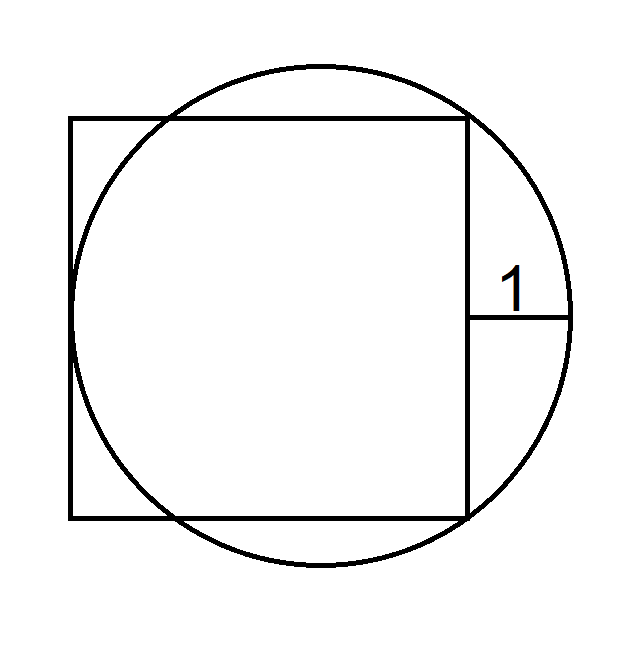
Mikä on neliön pinta-ala?
Ratkaisuni kannalta tarkastelen seuraavaa kaaviota.
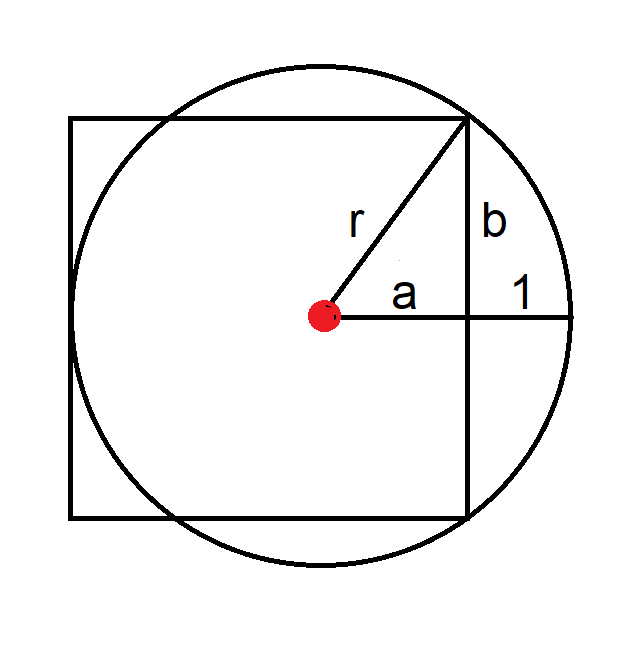
Tässä on ratkaisuni (PDF).
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .


