Kysy velholta #399
Jos poistat pienen neliön ensimmäisestä kuvasta ja järjestelet palat uudelleen, kokonaispinta-ala näyttää silti samalta. Miten tämä on mahdollista?
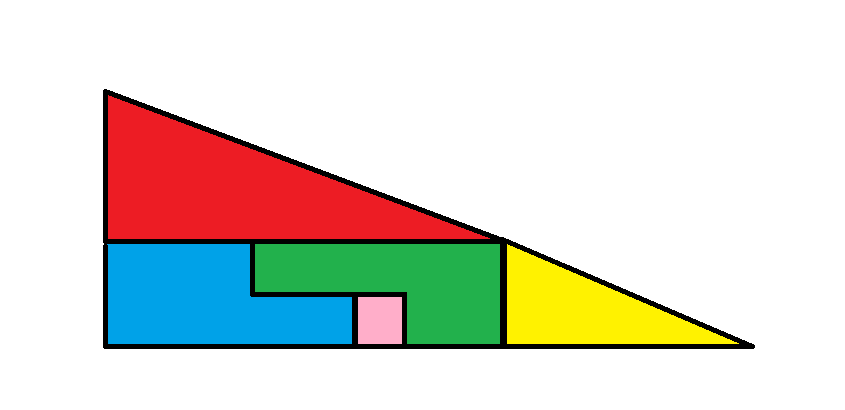
Kuva 1
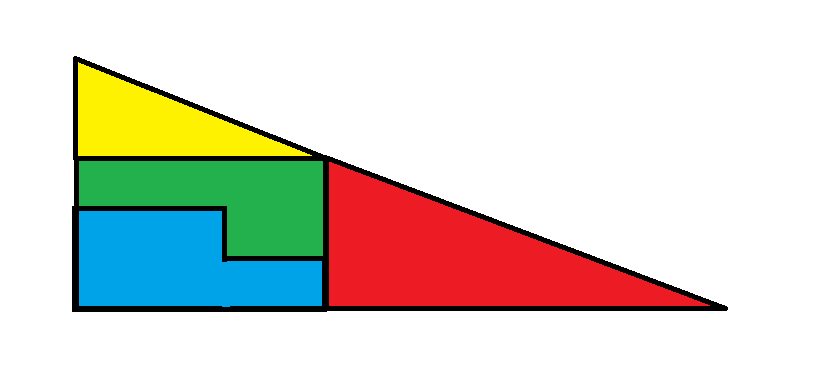
Kuva 2
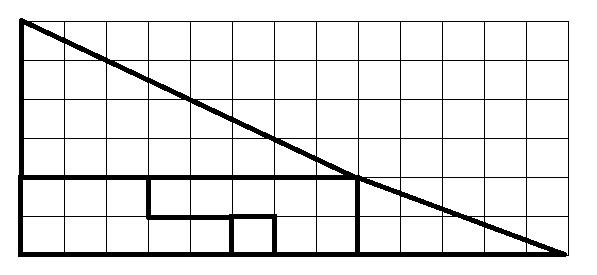
Yllä oleva kuva näyttää ensimmäisen kuvan ruudukossa, jotta kunkin palan koko näkyy paremmin.
Huomaa, että ison punaisen kolmion sivut ovat pituudeltaan 4 ja 8. Huomaa seuraavaksi, että pienemmän keltaisen kolmion sivut ovat pituudeltaan 2 ja 5. Toisin sanoen kolmiot eivät ole verrannollisia. Kahden kolmion hypotenuusalla ei ole samaa kulmakerrointa kuin kummassakaan kuvassa. Toisen kulmakerroin on 0,5 ja toisen 0,4. Palasten sijoittaminen tällä tavalla kummassakin kuvassa näyttää siltä, että ne muodostavat suuren kolmion, jonka sivut ovat 5 ja 13, mutta se ei ole kolmio.
Punaisen kolmion pinta-ala on 4 * 8/2 = 16.
Keltaisen kolmion pinta-ala on 2 * 5 / 2 = 5.
Ensimmäisessä kuvassa kolme muuta palaa muodostavat 2 x 8 kokoisen suorakulmion, jonka kokonaispinta-ala on 16.
Toisessa kuvassa kaksi muuta palaa muodostavat 3 x 5 kokoisen suorakulmion, jonka kokonaispinta-ala on 15.
Ensimmäisen kuvan kokonaispinta-ala on punainen kolmio + keltainen kolmio + iso suorakulmio = 16 + 5 + 16 = 37.
Toisen kuvan kokonaispinta-ala on punainen kolmio + keltainen kolmio + pieni suorakulmio = 16 + 5 + 15 = 36.
Yhteenvetona voidaan todeta, että ensimmäinen kuva on suurempi pienen neliön vuoksi. Molemmissa tapauksissa on kyse optisesta harhasta, että palaset muodostavat yhdessä suuren kolmion. Näin ei kuitenkaan ole.
Suuren aavikon reunalla on 16 moottoripyörää. Jokainen moottoripyörä voi kulkea 160 kilometriä yhdellä polttoainesäiliöllä. Kaikki moottoripyörät lähtevät liikkeelle täydellä tankilla. Polttoaineen siirtäminen moottoripyörien välillä on sallittua. Tavoitteena on saada yksi moottoripyörä mahdollisimman kauas lähtöpisteestä. Kuinka pitkälle se voi päästä?
Ongelman ydin on, että ryhmä ajaa lyhyen matkan. Sitten he ottavat loput polttoaineesta yhdestä moottoripyörästä ja täyttävät muiden tankit.
Esimerkiksi alussa jaetaan täysi bensatankki 16 osaan, yksi kutakin moottoripyörää kohden. Sitten kaikki ajavat yhdessä, kunnes 1/16 tankillisesta on kulunut loppuun, jolloin ryhmän yhteismatkaksi saadaan 100/16 = 6,25 mailia. Ota yhden moottoripyörän tankillinen 15/16 ja kaada 1/16 tankillisesta muihin 15 moottoripyörään, jolloin ne täyttyvät täsmälleen.
Toista sitten sama prosessi, mutta 15 moottoripyörää jäljellä pitäen aja niin pitkälle kuin 1/15 tankillista vie, eli 100/15 = 6,666667 mailia. Ota sitten toiset 14/15 tankillista yhdestä moottoripyörästä ja pumppaa 1/15 tankista muihin 14 moottoripyörään.
Jatkamalla tätä prosessia viimeisen moottoripyörän kokonaismatkaksi saadaan (1/16) + (1/15) + (1/14) + ... + (1/1) =~ 338,072899 mailia.
Tätä kysymystä esitettiin ja siitä keskusteltiin foorumillani Wizard of Vegasissa .
Mitä mieltä olet Prinsessa Ruususen paradoksista?
Muiden lukijoiden tiedoksi, tässä on mitä Prinsessa Ruususen ongelmassa/paradoksissa kysytään.
Prinsessa Ruusunen (SB) tarjoutuu vapaaehtoiseksi kokeeseen. Kaikki kokeen yksityiskohdat selitetään hänelle totuudenmukaisesti seuraavasti:
- Sunnuntai: SB nukutetaan. Kun hän nukahtaa, heitetään reilu kolikko.
- Maanantai: SB herätetään maanantaina ja kysytään: "Mikä on todennäköisyys, että kolikko osui kruunaan?" Vastattuaan hänet nukahdetaan uudelleen amnesialääkkeellä, joka saa hänet unohtamaan kaiken maanantaina tapahtuneen.
- Tiistai: Jos kolikko putosi klaavalle, sama asia tapahtuu uudelleen kuin maanantaina. Jos kolikko putosi kruunalle, hän nukkuu koko päivän.
- Keskiviikko: SB herätetään uudelleen, häneltä ei kysytä mitään, ja hän menee kotiin kokeen päätyttyä.
Kysymys kuuluu, miten hänen pitäisi vastata maanantaina ja kenties tiistaina esitettyyn kysymykseen?
Vastaukseni
Jos tämä koe toistettaisiin miljoona kertaa, voisimme odottaa näkevämme kolmenlaisia heräämisiä, joista jokainen on yhtä todennäköinen:
- Kolikko osuu päähän, herää maanantaina.
- Kolikko laskeutuu hännälle ja herää maanantaina.
- Kolikko laskeutuu hännälle ja herää tiistaina.
Tämä johtuu siitä, että maanantain heräämisten tulisi jakautua tasan kruunan ja klaavan heittojen kesken. Jos kolikko osuu kruunaan, maanantain ja tiistain heräämiset ovat täsmälleen yhtä monta. Näin ollen kaikilla kolmella ryhmällä on suunnilleen sama määrä heräämisiä suurella otoskoolla.
Näistä heräämisistä yksi kolmesta tapahtuu kruunan kääntämisen jälkeen. Näin ollen todennäköisyys sille, että kolikko osuu kruunaan, on 1/3.
Puolikas leiri väittää, että SB:lle ei anneta lisätietoja jokaisen heräämisen yhteydessä, ja siksi sen pitäisi olettaa, että jokainen käänteen lopputulos oli yhtä todennäköinen.
Laajentaisin ongelman 999 999 heräämiseen, jos kolikko osuu klaavaan. Vain yksi miljoonasta heräämisestä tapahtuisi kruunan käännön jälkeen. Joten olisi melko helppo olettaa, että minkä tahansa heräämisen yhteydessä se olisi todennäköisesti yksi 999 999 heräämisestä klaavan käännön jälkeen. Toisin sanoen oikea vastaus tässä tapauksessa olisi yksi miljoonasta.
Tarjotakseni toisen laajennuksen, entä jos SB:tä pyydettäisiin ennustamaan kolikonheitto jokaisella heräämisellä? Jos hän osuisi oikein, hän voittaisi 1 000 dollaria. Jos hänellä olisi strategia sanoa "kruuna", hän voisi odottaa voittavansa (1/2) * 1 000 dollaria = 500 dollaria. Jos hänellä olisi strategia sanoa "klaava", hän voisi odottaa voittavansa (1/2) * 2 000 dollaria = 1 000 dollaria. Joten jo se, että SB herää, suosii kolikon osumista klaavaan.
Jos selitykseni ei ollut selkeä, Wikipedian Ruususen ongelma syventyy asiaan paljon syvällisemmin kuin minä, ja siinä on mukana muita mahdollisia vastauksia SB:ltä.
Tätä kysymystä esitettiin ja siitä keskusteltiin foorumillani Wizard of Vegasissa .


