Kysy velholta #405

Olkoon y = molemmat lausekkeet. Näin ollen meillä on:

• y = x^2 - 3
• y = neliöjuuri(x+3)

Huomaa luku 3 molemmissa lausekkeissa. Esitetään molemmat yhtälöt siten, että toisella puolella on luku 3. Ensin meillä on:

3 = x^2 - y

Seuraavaksi neliöidään yllä oleva toinen yhtälö:

y^2 = x+3

3 = y^2 - x

Yhtälöidään molemmat lausekkeet luvulla 3:

x^2 - y = y^2 - x

Järjestetäänpä uudelleen:

x^2 - y^2 + x - y = 0

(x + y)(xy) + x - y = 0

(xy)(x + y + 1) = 0

Tarkastellaan ensin xy = 0:

xy = 0

Korvataan y arvolla y = x^2 - 3.

x - (x^2 - 3) = 0

x^2 - x - 3 = 0

Pythagoraan kaavan avulla:

x = (1 +/- neliöjuuri(1 + 12)/2

x = (1 + neliöjuuri(13)/2 & x = (1 - neliöjuuri(13)/2

Toiseksi, tarkastellaan x+y+1 = 0:

Korvataan y arvolla y = x^2 - 3.

x + (x^2 - 3) + 1 = 0

x + x^2 - 3 + 1 = 0

x^2 + x - 2 = 0

Pythagoraan kaavan avulla:

x = (-1 +/- neliöjuuri(1 + 8)/2

x = (-1 +/- 3)/2

x = 1, x = -2

Joten neljä vastaustamme ovat:

• x = 1
• x = -2
• x = (1 + neliöjuuri(13)/2 = ~ 2,302776
• x = (1 - neliöjuuri(13)/2 =~ -1,302776

Haluan kiittää SyberMathin YouTube-videota Solving x^2-3=sqrt(x+3) tästä menetelmästä tämän tehtävän ratkaisemiseksi. Siirry kohtaan 6:28, jossa kerrotaan tästä menetelmästä.

[spoiler=Ratkaisu] Tarkastellaan tätä kaaviota ratkaisuna.

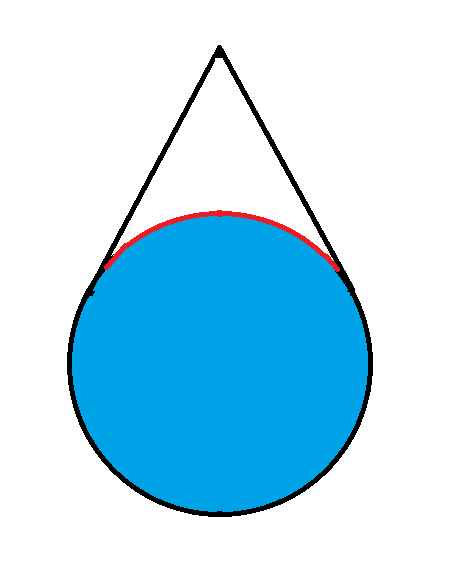
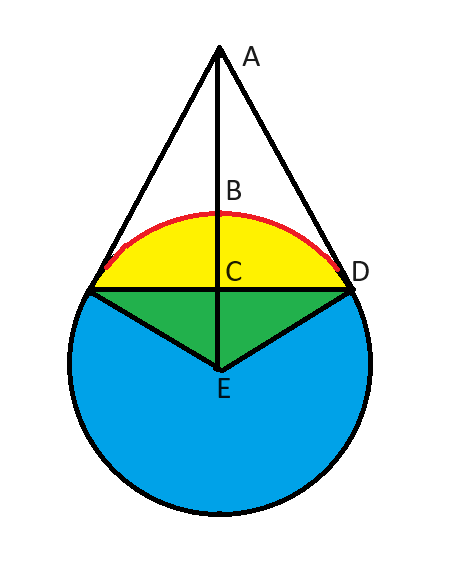
Tarkastellaan kolmiota ADE. Tiedämme:

• Kulma ADE on 90 astetta, koska AD on ympyrän tangentti.
• Kulma AED on 60 astetta, koska vihreän kolmion kulma E:ssä on 120 astetta (1/3 koko 360:sta).
• Kulman EAD on oltava kolmion ADE muut 30 astetta.

Tämä on klassinen 30-60-90 kolmio. Meidän kaikkien tulisi tietää, että kyseisen kolmion sivut ovat verrannollisia lukuihin 1, 2 ja neliö(3).

Tässä tapauksessa ED = 1, kuten kysymyksessä on annettu. AE on kaksinkertainen etäisyys eli 2.

2 on etäisyys pisteestä ympyrän keskipisteeseen. Meiltä kysytään etäisyys pisteestä lähimpään ympyrän pisteeseen. Joten vähennämme säteen. Vastaus on siis 2 - 1 = 1.

[/spoileri]

Muista etäisyys = nopeus * aika, jonka ilmaisemme muodossa d = r*t

Kirjoitetaanpa se uudelleen: t = d/r.

Aika on sama sekä Bobissa että sillan alussa kohtaavan junan kohdalla:

Annetaan mennä:

• x = junan lähtöpisteen ja sillan alun välinen etäisyys.
• r = junan nopeus

Tarkastellaan ensin Bobia, joka juoksee takaisin. Ilmaistaan t siten, että sekä Bob että juna kohtaavat sillan alussa:

Bob: t = (1/3)/5

Juna: t = x/r

Yhtälöimällä kaksi lauseketta t:lle:

r/3 = 5x

r = 15x

Toiseksi, katsotaanpa Tomia, joka juoksee edellä. Ilmaistaan t siten, että sekä Tom että juna kohtaavat sillan alussa:

Tom: t = (2/3)/5

Juna: t = (1+x)/r

Yhtälöimällä kaksi lauseketta t:lle:

(2/3)/5 = (1 + x)/r

2r/3 = 5(1 + x)

2r = 15(1 + x)

2r = 15 + 15x

Tässä vaiheessa meillä on:

• r = 15x
• 2r = 15 + 15x

Sijoitetaan ensimmäisen yhtälön r-lauseke toiseen:

30x = 15 + 15x

15x = 15

x = 1

Muista, r = 15x.

Joten junan nopeus on 15 * 1 = 15 mph.