Kysy velholta #410

Q: Nathan ostaa 45 kiloa papuja. Pavut koostuvat 99 painoprosenttia vedestä. Hän jättää ne aurinkoon kuivumaan. Seuraavana päivänä hän huomaa, että ne koostuvat 98-prosenttisesti vedestä. Mikä on niiden uusi paino?

<div><button onclick='var btn = this; var div = btn.parentNode.childNodes[1]; if (div.style.display != "block") { div.style.display="block"; } else { div.style.display="none"; }' style='padding:2px 4px;'>Vastaus</button><div class='spoiler'>50 paunaa</div></div> [spoiler=Ratkaisu] Olkoon:<ul><li> w = Alkuperäinen veden paino.</li><li> w&#39; = veden paino papujen kuivaamisen jälkeen.</li><li> x = Kaiken muun pavuissa olevan paino.</li></ul> Ensimmäiseksi päiväksi meille annetaan: w + x = 100 w/(w+x) = 0,99 Sijoittamalla ensimmäinen yhtälö toiseen: w/100 = 0,99 w = 99 Näin ollen x=1. Seuraavana päivänä meille annetaan: w&#39;/(w&#39; + x) = 0,98 w&#39; = 0,98 * (w&#39; + x) 0,02w&#39; = 0,98x Tiedämme, että x=1, joten: 0,02w&#39; = 0,98 w&#39; = 0,98/0,02 = 49 Kokonaispaino seuraavana päivänä on x + w&#39; = 1 + 49 = 50. [/spoileri]

Näen, että vastasit kysymykseen Plinko-pelistä Hinta on oikea -osiossa Kysy velholta -palstalla #115 . He kuitenkin joskus muuttavat palkintosummia erikoisohjelmien aikana. Esimerkiksi Big Money Weekillä palkinnot vasemmalta oikealle olivat 500 dollaria, 1000 dollaria, 2500 dollaria, 0 dollaria, 200 000 dollaria, 0 dollaria, 2500 dollaria, 1000 dollaria ja 500 dollaria. Mikä olisi odotusarvo kullekin pelipaikalle, josta kiekko pudotetaan? Mikä on todennäköisyys, että kiekko laskeutuu mihin tahansa palkintoon millä tahansa aloituspelipaikalla?

anonyymi

Kiekon pudotukseen on yhdeksän lähtökohtaa. Meidän tarvitsee kuitenkin keskittyä vain viiteen, koska palkinnot ja tappien asettelu ovat symmetrisiä. Merkitään ne vasemmasta reunasta alkaen numeroilla 1–5.

Myös yhdeksän loppuasentoa on, nimetäänpä viisi ensimmäistä vasemmalta alkaen myös numeroilla 1–5.

Seuraava taulukko näyttää todennäköisyyden laskeutua mihin tahansa paikkaan (vasen sarake) riippuen siitä, mistä pudotuspaikasta (ylempi rivi).

Laskeutumispaikka	Pudota 1 tai 9	Pudota 2 tai 8	Pudota 3 tai 7	Pudota 4 tai 6	Pudota 5
1 tai 9	0,225586	0,193359	0.121094	0,056641	0,032227
2 tai 8	0.386719	0.346680	0,250000	0,153320	0.113281
3 tai 7	0.242188	0,250000	0,257813	0,250000	0.242188
4 tai 6	0.113281	0,153320	0,250000	0.346680	0.386719
5	0,032227	0,056641	0.121094	0,193359	0,225586
Kokonais	1.000000	1.000000	1.000000	1.000000	1.000000

Seuraava taulukko näyttää odotetun arvon jokaisesta pudotuspaikasta kysymälläsi Big Money Weekillä. Kuten odotettua, pelaajan pitäisi pudottaa kiekko suuntaansa suurimman palkinnon päälle.

Pudotuspaikka	Odotettu voitto
1 tai 9	7 550,29 dollaria
2 tai 8	12 396,48 dollaria
3 tai 7	25 173,83 dollaria
4 tai 6	39 478,52 dollaria
5	45 852,05 dollaria

Mikä on Gabrielin sarven paradoksi?

anonyymi

Tarkastellaan ensin yhtälön y=1/x mukaista käyrää x:n arvoille 1:stä äärettömyyteen. Kaavio näyttää seuraavalta x:n arvoille 17:ään asti.

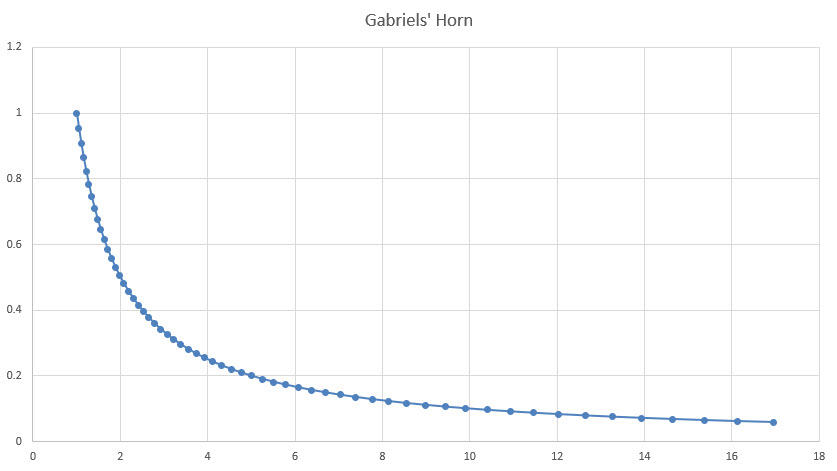
Kuvittele seuraavaksi, että käyrää kierretään x-akselin ympäri. Se luo sarven näköisen hahmon, jolla on äärettömän pitkä pää. Sitäkö matemaatikot kutsuvat Gabrielin sarveksi?

Kuvan lähde: Matematiikan sielu .

Seuraavaksi tarkastellaan Gabrielin sarvea koskevia kysymyksiä:

Mikä on tilavuus?
Mikä on pinta-ala?

Tässä ovat vastaukset:

[spoiler=Vastaus]

Tilavuus = π = pii.
Pinta-ala = ääretön

[/spoileri]

Työni, joka näyttää vastaukset, löytyy täältä (PDF).

Paradoksin luonne kysyy, kuinka tilavuus voi olla äärellinen, mutta pinta-ala ääretön?

Havaittu paradoksi syntyy, kun sekoitamme kaksi ulottuvuutta kolmeen. Meidän ei yksinkertaisesti pitäisi tehdä niin. Tarkastellaan ympyrää A, jonka säde on 1, ja ympyrää B, jonka säde on 1,1, missä ympyrä A on ympyrän B sisällä.

Ympyrän A ympärysmitta on 2*pii =~= 6,283185 ja ympyrän B pinta-ala on 1,1^2 * pi =~ 3,801327. Huomaa, että ympyrä B on suurempi kuin ympyrä A, mutta sen pinta-ala on pienempi kuin ympyrän B ympärysmitta. Kyse ei ole siitä, että ympyrän B ympärysmitta olisi osa ympyrän A pinta-alaa. Pinta-ala ja ympärysmitta ovat eri mittoja eri ulottuvuuksissa, eikä niitä pitäisi verrata.

Toinen tapa tarkastella asiaa on, että jos tekisimme ympyrästä A levyn, jossa on ääretön määrä uria, näiden urien pituus olisi ääretön.

Palatakseni Gabrielin torveen, tarkastellaan sen yksinkertaistamista diskreettiseen tapaukseen, jossa ympyrät ovat säteeltään 1, 1/2, 1/3, 1/4 ...

Näiden ympyröiden tilavuuksien summa olisi pi*(1/1 + 1/4 + 1/9 + 1/16 + ...). On olemassa tunnettu ääretön sarja, joka sanoo:

1/1 + 1/4 + 1/9 + 1/16 + ... = pi^2/6 =~ 1,644934.

Lisäämällä toisen pii-termin, ympyröiden pinta-alojen summa on pi^3/6 =~ 5,167713.

Samaan aikaan ympärysmittojen summa on 2*pii(1/1 + 1/2 + 1/3 + 1/4 + ...).

Matematiikassa on toinen tunnettu ääretön sarja, jota kutsutaan harmoniseksi sarjaksi ja joka kuuluu seuraavasti:

1/1 + 1/2 + 1/3 + 1/4 + ... = ∞ = ääretön.

2*pii*∞ on edelleen yhtä kuin ∞.

Jos laajennamme tätä logiikkaa äärettömän pieniin ympyröiden välisiin etäisyyksiin, saamme Gabrielin torven.

Nathan ostaa 45 kiloa papuja. Pavut koostuvat 99 painoprosenttia vedestä. Hän jättää ne aurinkoon kuivumaan. Seuraavana päivänä hän huomaa, että ne koostuvat 98-prosenttisesti vedestä. Mikä on niiden uusi paino?

anonyymi

50 paunaa

[spoiler=Ratkaisu]

Olkoon: