WOO logo

Velho suosittelee

Kysy velholta #413

Onko olemassa tapaa tehdä Secret Santa -lahjojen vaihto, joka täyttää seuraavat vaatimukset?

  • Kukaan ei anna lahjaa itselleen.
  • Ei ole kertakäyttömahdollisuuksia.
  • Kukaan ei tiedä mitään muuta kuin kenelle heidän pitäisi ostaa.
  • Jokainen ottelu on yhtä todennäköinen.

anonyymi

Kyllä! Kutsun seuraavaa Hannah Fryn metodiksi.

  • Luo alla olevan kuvan mukainen korttisarja. Jokaisella kortilla tulee olla yksilöllinen numero ylä- ja alareunassa. Alla olevassa esimerkissä numero on 23.
  • Sekoita kortit ja laita ne takaisin pinoon.
  • Pidä pino ehjänä ja leikkaa jokainen kortti keskeltä linjaa pitkin, jolloin muodostuu kaksi pinoa.
  • Leikkaa ja viimeistele YHDEN pinon leikkaus.
  • Jaa kunkin pinon päällimmäinen kortti yksi kerrallaan jokaiselle osallistujalle.
  • Tee numeroitu lista ja pyydä kaikkia kirjoittamaan siihen oma numeronsa.

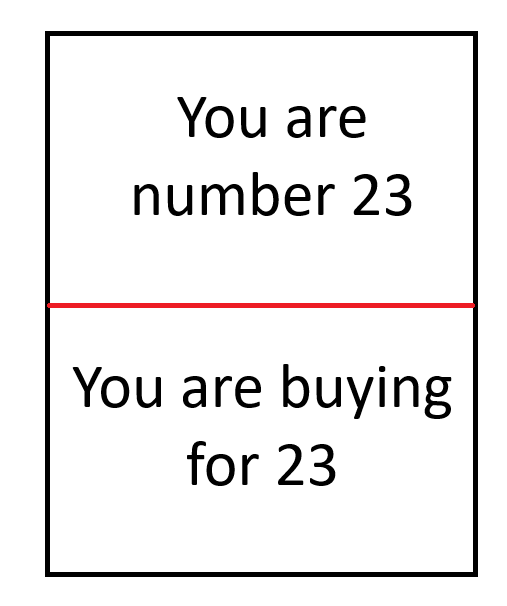
Tämän menettelyn jälkeen jokaisella on kaksi korttia, joissa lukee esimerkiksi "Olet numero 13" ja "Ostat numerolle 7". Kun lista on täytetty, kaikki tietävät, kenelle ostaa, mutta heillä ei ole aavistustakaan, kuka ostaa heille.

Lähde: Ongelmat salaisen joulupukin kanssa - Numberphile .

Uima-allas on täynnä suolavettä. Altaassa on 1000 kuutiometriä vettä. Puutarhaletku päästää makeaa vettä altaaseen yhden kuutiometrin tunnissa. Kun makeaa vettä virtaa sisään, vesi virtaa ulos toisesta päästä samalla nopeudella. Kuinka kauan kestää, että altaassa on enää 1 % suolavettä?

anonyymi

Vastaus on 2000 ln(10) =~ 4605,170186 tuntia =~ 191,8821 päivää.

Tässä on ratkaisuni (PDF).

Kuinka monta vieritystä keskimäärin tarvitaan kullakin platonisella kappaleella, jotta mikä tahansa aiemmin vieritetty sivu saadaan vieritettyä?


Kuvalähde: Wikipedia

anonyymi

Tässä on vastaus sivujen lukumäärän mukaan.

Sivut Keskimääräiset rullat
4 3.218750
6 3.774691
8 3.846558
12 5.036074
20 6.293585

Selvitetään vain kuusisivuisen kuution tapaus.

  • Todennäköisyys sille, että koe päättyy kahteen heittoon, on 1/6.
  • Todennäköisyys sille, että koe päättyy kolmeen heittoon, on (5/6) * (2/6).
  • Todennäköisyys sille, että koe päättyy neljään heittoon, on (5/6)*(4/6)*(3/6).
  • Todennäköisyys sille, että koe päättyy viiteen heittoon, on (5/6)*(4/6)*(3/6)*(4/6).
  • Todennäköisyys sille, että koe päättyy kuuteen heittoon, on (5/6)*(4/6)*(3/6)*(2/6)*(5/6).
  • Todennäköisyys sille, että koe päättyy seitsemään heittoon, on (5/6)*(4/6)*(3/6)*(2/6)*(1/6)*(6/6).

Olkoon pr(n) = todennäköisyyskoe päättyy n heittoon.

Odotusarvo heitoille on: 2*pr(2) + 3*pr(3) + 4*pr(4) + 5*pr(5) + 6*pr(6) + 7*pr(7) =

2*(1/6) + 3*(5/6)*(2/6) + 4*(5/6)*(4/6)*(3/6) + 5*(5/6)*(4/6)*(3/6)*(4/6) + 6*(5/6)*(4/6)*(3/6)*(2/6)*(5/6) + 7*(5/6)*(4/6)*(3/6)*(2/6)*(1/6)*(6/6) =~ 3,774691358.