WOO logo

Velho suosittelee

Kysy velholta #415

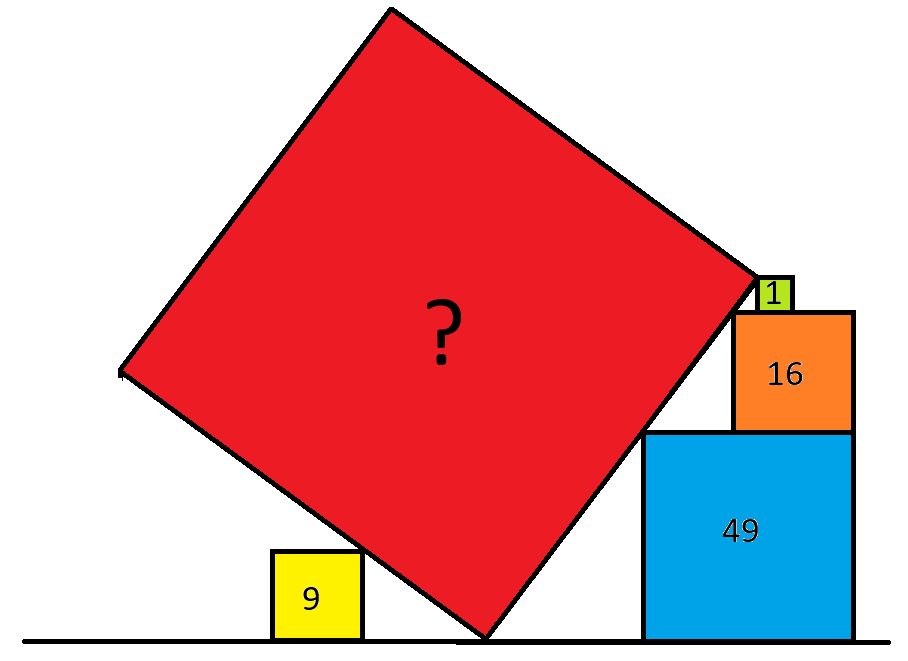
Yllä olevassa kuvassa numerot edustavat neljän neliön pinta-aloja. Mikä on punaisen neliön pinta-ala?

anonyymi

225

[spoiler=Ratkaisu]

Ensinnäkin, keltainen neliö ei auta meitä lainkaan. Se on harhaanjohtava merkki, joten jätetään se huomiotta.

Tarkastellaan seuraavaksi oranssin neliön vasemmalla puolella olevaa kolmiota, kuten seuraavassa kuvassa näkyy.

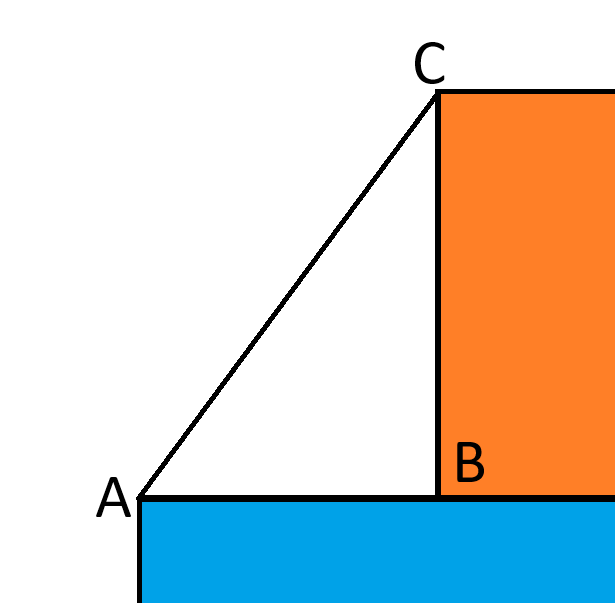
BC = neliöjuuri(16) = 4.

AB = sqrt(49) - sqrt(16) = 7-4 = 3.

Pythagoraan kaavan mukaan AC2 = 42 + 32 = 25.

AC = neliöjuuri(25) = 5.

Kaikkien kolmen oikealla puolella olevan neliön korkeus on sqrt(49) + sqrt(16) + sqrt(1) = 12.

Punaisen neliön sivun pituuden suhde oikeanpuoleisten kolmen neliön korkeuden korkeuteen on sama kuin AC:n ja BC:n suhde = 5/4.

Punaisen neliön sivun pituus on siis (5/4) * 12 = 15.

Punaisen neliön pinta-ala on siis 15 2 = 225.

Samankaltaista pulmaa kysytään ja siitä keskustellaan foorumillani Wizard of Vegasissa .

Mind Your Decisions -YouTube-kanavalla on myös samanlainen pulmapeli.

[/spoileri]

Mikä on pienin mahdollinen suorakulmio, jonka pinta-ala on yhtä suuri kuin sen kehä?

anonyymi

Suorakulmion mitat ovat 4x4 ja sen pinta-ala ja kehä on 16.

[spoiler=Ratkaisu]

Olkoot suorakulmion mitat x ja y.

Meille on annettu: xy = 2x + 2y.
2y - xy = 2x
y(2 - x) = 2x
y=2x/(2-x)

Olkoon f(x) = Suorakulmion pinta-ala = x*y =
x * 2x / (2 - x) = 2x 2 / (2 - x)

Pienimmän pinta-alan löytämiseksi ota derivaatta osamääräsäännön avulla:

f'(x) = 4x(2 - x) + 2x² / (2 - x) ² = 0

4x(2 - x) + 2x 2 = 0

8x = 2x 2

x=4

Jos x=4, y = 2*4/(4-2) = 8/2 = 4.

Ratkaistaan y muille x:n arvoille lähellä arvoa 4.

Jos x=3, y=6 ja pinta-ala on 18

Jos x=5, y = 10/3, ja pinta-ala on 16+(2/3).

On helppo nähdä, että ratkaisu kohdissa x=4 ja y=4 johtaa minimiin. Näin ollen pienin mahdollinen suorakulmio on 4x4 = 16.

[/spoileri]

Kasinon arvonnassa rummussa on seuraava määrä lippuja lipunhaltijan toimesta:

  • Pelaajalla 1 on 6 lippua.
  • Pelaajalla 2 on kaksi lippua.
  • Pelaajalla 3 on yksi lippu.
  • 21 muulla pelaajalla on 21 lippua.

Kasino arpoo viisi lippua, joissa on viisi samanarvoista palkintoa. Jokainen pelaaja voi voittaa vain kerran. Jos lipun arpoo pelaaja, joka on jo voittanut, kyseinen lippu hylätään ja tilalle arvotaan uusi lippu.

Pelaajat 1, 2 ja 3 sopivat jakavansa voittonsa arvonnassa saamansa osuuden mukaisesti. Mikä on reilu jako?

Mukke

Yksinkertaistan ongelmaa olettamalla, että jos lipun arpoo pelaaja, joka on jo voittanut, palkinto mitätöidään. Muuten matematiikka menee aivan liian sotkuiseksi ja vaatii käytännössä satunnaisen simulaation.

Todennäköisyys sille, että n lipulla varustettu pelaaja EI voita palkintoa, on combin(30 - n, 5) / combin(30, n).

Näin ollen todennäköisyys, että pelaaja A tekee palkinnon, on 1-combin(24,5)/combin(30,5) = 0,701739.

Näin ollen todennäköisyys, että pelaaja B tekee palkinnon, on 1-combin(28,5)/combin(30,5) = 0,310345.

Näin ollen todennäköisyys, että pelaaja C tekee palkinnon, on 1-combin(29,5)/combin(30,5) = 0,166667.

Näiden todennäköisyyksien summa on 1,178750. Se on kuinka monta voittoa ryhmä voi odottaa saavansa.

Mielestäni jokaisen pelaajan tulisi saada osuus, joka vastaa hänen voittotodennäköisyyttään jaettuna ryhmän odotetulla kokonaisvoitolla.

A saa 0,701739/1,178750 = 0,595324 osaketta.

B saa 0,310345/1,178750 = 0,263283 osaketta.

C saa 0,166667/1,178750 = 0,141393 osaketta.

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .