Kysy velholta #419
Huomaan, ettei sinulla ole videopokeristrategioita, joissa olisi suurempi voitto peräkkäisestä kuninkaallisesta. Voitko auttaa minua siinä?
Selvennetäänpä ensin videopokeriin liittyvää terminologiaa.
- Peräkkäinen kuninkaallinen = vain alhaalta ylös (10-JQKA)
- Käännettävä kuninkaallinen = Molemmat suunnat (10-JQKA tai AKQJ-10)
Asiaa tekee vielä hämmentävämmäksi se, että kaikki eivät käytä tätä terminologiaa, ja peli, jossa on erillinen rivikohta peräkkäiselle kuninkaalliselle voitolle, saattaa maksaa voitot molempiin suuntiin. Toivottavasti sääntönäytöt selventävät tätä.
Tästä huolimatta helppo ja täydellinen tapa pelata käsi, jolla on mahdollinen peräkkäinen tai palautuva kuninkaallinen arvo, on syöttää se videopokerilaskuriini. Tässä linkit:
Jos et voi tai halua käyttää sivustoani automaatilla, huomioi tässä keskimääräiset voitot kuninkaalliselle kortille, kun käännettävä kuninkaallinen kortilla saa 50 000 5 kreditin panoksesta riippuen siitä, kuinka monta korttia on jo pelissä.
- 4 käännettävään kuninkaalliseen = 10 000
- 3 käännettävään kuninkaalliseen = 5 400
- 2 käännettävään kuninkaalliseen = 2 333
- 1 käännettävään kuninkaalliseen (keskiasento) = 1 567
- 1 käännettävään kuninkaalliseen (ei keskiasentoon) = 1,183
- 0 käännettävään kuninkaalliseen = 800
Peräkkäisissä kuninkaallisissa peleissä (jotka maksavat vain pienestä suureen) käytä lukua 1 183 sijoituksesta riippumatta.
Näiden lukujen avulla käytä videopokeristrategiatyökaluani ja luo erillinen strategia jokaiselle keskimääräiselle kuninkaalliselle voitolle. Käytä sitten strategiaa koneella sen mukaan, kuinka monta kuninkaallista korttia on oikeassa asennossa.
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Kellogg'silla on uusia pallomaisia versioita Apple Jacksista, Frosted Flakesista ja Kravesta, ja heidän mukaansa muoto antaa enemmän lasitetta. Itse asiassa he sanovat: "Teimme laskelman." Tekivätkö he sen oikein?

Ei!!!!!!!! Ei, he eivät tehneet laskelmia oikein. Itse asiassa pallo on HUONOIN kolmiulotteinen muoto, jos he haluavat maksimoida pinta-alan ja tilavuuden suhteen.
Aloitetaan tarkastelemalla laatikon takana olevia pinta-alayhtälöitä.

He kyllä ilmoittavat oikein pallon, tai sen, mitä he luultavasti kutsuisivat donitsinreiäksi, pinta-alan olevan 4πr2 , jossa r = säde.
He kuitenkin ilmoittavat virheellisesti toruksen, jota he luultavasti kutsuisivat donitsiksi, pinta-alaksi 2π 2 rR. Todellinen kaava on kaksinkertainen eli 4π 2 rR. Katso seuraavasta kuvasta r ja R.
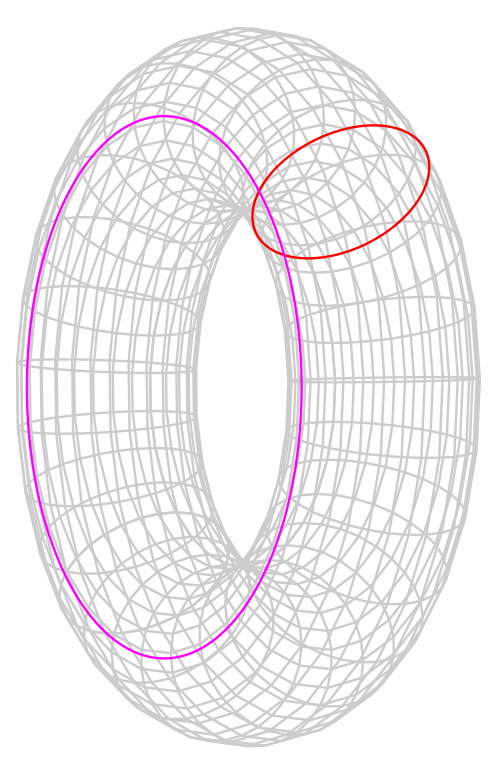
r = punaisen ympyrän säde
R = etäisyys toruksen lähimmästä osasta keskipisteeseen.
Kuvan lähde: Wikipedian sivu toruksesta .
Voisi sanoa, että pallon vaihtoehto on lasitteen levittäminen vain puolelle torusta, kuten kuorrutetta donitsiin. Lähetän kuitenkin tarkemman tarkastelun toruksen muotoisesta perinteisestä Apple Jacks -leivoksesta, jossa lasite levitetään koko donitsiin.
Seuraavaksi haluan esittää myös kaavat sekä pallon että toruksen tilavuuksille.
- Pallo = (4/3) πr3
- Torus = 2π²r²R
Muistutuksena, pinta-alan kaava on tilavuuden derivaatta.
Toruksen, jonka r=1 ja R=1, pinta-alaksi saadaan 39,478418 ja tilavuudeksi 19,739209. Pinta-alan suhde tilavuuteen eli lasitesuhde on mielenkiintoista kyllä tasan 2.
Tilavuuden yhtäläistämiseksi pallon säteen pitäisi olla 1,676539. Pallon tälle säteelle saadaan pinta-ala 35,321350 ja tilavuus 19,739209. Pinta-alan suhde tilavuuteen eli lasitesuhde on 1,789400.
Toisin sanoen torus tarjoaa enemmän pinta-alaa tai lasitetta samalle tilavuudelle.
Mainitsin aiemmin, että pallo on huonoin kolmiulotteinen muoto, jonka tavoitteena on maksimoida pinta-alan suhde tilavuuteen. Tätä kutsutaan isoperimetriseksi epäyhtälöksi . Vaikka tämä on todistettu, mielestäni se on itsestään selvää. Esimerkiksi kuplat pyrkivät minimoimaan pinta-alan ja maksimoimaan lujuuden, ja ne ovat muodoltaan pallomaisia.
Loppujen lopuksi sinun kannattaa hankkia pallomainen tai donitsinmuotoinen versio Apple Jacksista tai jostain muusta, jos haluat minimoida glaseerin käytön, etkä maksimoida sitä. Se olisi tavoitteeni, koska mielestäni nämä murot ovat aivan liian makeita ja ottaisin mielelläni vähemmän glaseeria. Moitin myös ehdottomasti Kellogg'sia harhaanjohtavasta mainonnasta, josta he saavat harvinaisen häpeän osoituksena Wizard-sormenheiluttelun.
Tätä kysymystä on kysytty ja siitä keskustellaan Wizard of Vegas -foorumillani .
Lisätietoja varten suosittelen MindYourDecisions-kanavan Presh Talwalkarin (yksi suosikeistani!) YouTube-videota Internet spots big missign on Kellogg's crease box .
Mikä on jaetun käden voittotodennäköisyys videopokerissa?
Ymmärrän, miten tämän kysymyksen vastauksella olisi käytännön sovellusta joissakin videopokerimuunnelmissa, jotka tarjoavat bonusominaisuuden, jos pelaaja saa voittavan käden jaossa.
Vastaus riippuu videopokerin muodosta. Seuraava taulukko näyttää kaikkien mahdollisten tapahtumien lukumäärän ja todennäköisyyden jaettaessa videopokeria 52 kortin pakalla ilman jokerikortteja, alkaen pienimmän voiton tuottavasta kädestä, joka on jätkäpari.
| Käsi | Yhdistelmät | Todennäköisyys |
|---|---|---|
| Kuningasvärisuora | 4 | 0,000002 |
| Värisuora | 36 | 0.000014 |
| Neloset | 624 | 0.000240 |
| Täyskäsi | 3 744 | 0,001441 |
| Huuhtele | 5 108 | 0,001965 |
| Suoraan | 10 200 | 0,003925 |
| Kolmoset | 54 912 | 0,021128 |
| Kaksi paria | 123 552 | 0,047539 |
| Jacks or Better | 337 920 | 0.130021 |
| Kaikki muut | 2 062 860 | 0,793725 |
| Kokonais | 2 598 960 | 1.000000 |
Jacks or Better -videopokeripelien voittokäden todennäköisyys on 0,206275.
Toinen taulukko näyttää kaikkien mahdollisten tapahtumien lukumäärän ja todennäköisyyden videopokerissa, jossa on 52 kortin pakka ja kakkoset ovat villejä, alkaen pienimmän voiton tuottavasta kädestä, joka on kolmoset.
| Käsi | Yhdistelmät | Todennäköisyys |
|---|---|---|
| Luonnollinen kuningasvärisuora | 4 | 0,000002 |
| Neljä kakkosta | 48 | 0.000018 |
| Villi kuningasvärisuora | 480 | 0.000185 |
| Viisi samanlaista | 624 | 0.000240 |
| Värisuora | 2 068 | 0,000796 |
| Neloset | 31 552 | 0.012140 |
| Täyskäsi | 12 672 | 0,004876 |
| Huuhtele | 14 472 | 0,005568 |
| Suoraan | 62 232 | 0,023945 |
| Kolmoset | 355 080 | 0.136624 |
| Kaikki muut | 2 119 728 | 0,815606 |
| Kokonais | 2 598 960 | 1.000000 |
Deuces Wild -videopokeripelien voittokäden todennäköisyys on 0,184394.
Kolmas taulukko näyttää kaikkien mahdollisten jakotapahtumien lukumäärän ja todennäköisyyden videopokerissa, jossa on 53 kortin pakka, mukaan lukien jokeri, alkaen pienimmän voiton tuottavasta kädestä, joka on kuningaspari.
| Käsi | Yhdistelmät | Todennäköisyys |
|---|---|---|
| viisi samanlaista | 13 | 0.000005 |
| kuningasvärisuora | 24 | 0.000008 |
| värisuora | 180 | 0.000063 |
| neloset | 3 120 | 0,001087 |
| täyskäsi | 6 552 | 0,002283 |
| huuhtelu | 7 804 | 0,002719 |
| suoraan | 20 532 | 0,007155 |
| Kolmoset | 137 280 | 0,047838 |
| 2 paria | 123 552 | 0,043054 |
| Kuninkaat tai paremmat | 262 956 | 0,091632 |
| Kaikki muut | 2 307 672 | 0.804155 |
| Kokonais | 2 869 685 | 1.000000 |
Jokeripokerissa (kuninkaat tai parempi) pelattavien videopokeripelien voittokäden todennäköisyys on 0,195845.


