WOO logo

Velho suosittelee

Kysy velholta #422

Väittelyn vuoksi oletetaan, että blackjack-pelissä on ääretön määrä pakkoja, ääretön uudelleenjako on sallittu, ja pelaaja jakaa minkä tahansa parin. Mikä on todennäköisyys sille, että pelaaja pelaa loppuun tietyn määrän käsiä?

anonyymi

Todennäköisyys uudelleenjaolle n kädelle on (combin(2*(n-1),n-1)/n) × (1/13)^(n-1) × (12/13)^n . Lisätietoja ensimmäisestä termistä, jonka kanssa tarvitsin apua, saat etsimällä katalaaniluvut .

Seuraava taulukko näyttää todennäköisyyden sille, että lopullisia jakoja on 1–20. Sekunti-sarake on "puiden" lukumäärä, joka on katalaaniluku yllä olevassa lausekkeessa.

Kädet Puut Todennäköisyys
1 1 0.9230769230769
2 1 0.0655439235321
3 2 0.0093080128093
4 5 0.0016523099661
5 14 0.0003285065968
6 42 0.0000699777366
7 132 0.0000156163334
8 429 0.0000036037693
9 1430 0.0000008529631
10 4862 0.0000002059225
11 16796 0.0000000505114
12 58786 0.0000000125531
13 208012 0.0000000031540
14 742900 0.0000000007998
15 2674440 0.0000000002045
16 9694845 0.0000000000526
17 35357670 0.0000000000136
18 129644790 0.0000000000035
19 477638700 0.0000000000009
20 1767263190 0.0000000000002

Kuulin, että Pythagoraan kolmikoita on ääretön määrä. Onko olemassa mitään kaavaa niiden löytämiseksi?

anonyymi

Kyllä, ainutlaatuisia Pythagoraan kolmikoita on ääretön määrä! Niille, jotka eivät tunne termiä, ne ovat suorakulmaisia kolmioita, joissa jokainen sivu on kokonaisluku. 3-4-5 on tunnetuin. Saadaksesi ainutlaatuisen (eli ei-pelkistettävän) Pythagoraan kolmikon, valitse mitkä tahansa kokonaisluvut a:lle ja b:lle, missä a < b ja yksi on pariton ja yksi on parillinen.

  • Osuus 1 = b 2 - a 2
  • Osuus 2 = 2ab
  • Hypotenuusa = a² + b²

Seuraava taulukko näyttää kaikki ei-reduktioituvat Pythagoraan kolmikot, joissa kaikki sivut ovat 101 tai vähemmän.

a, b Osuus 1 Osuus 2 Hypotenuusa
1,2 3 4 5
1,4 8 15 17
1,6 12 35 37
1,8 16 63 65
1,10 20 99 101
2,3 5 12 13
2,5 20 21 29
2,7 28 45 53
2,9 36 77 85
3,4 7 24 25
3,6 27 36 45
3,8 48 55 73
4,5 9 40 41
4,7 33 56 65
4,9 65 72 97
5,6 11 60 61
5,8 39 80 89
6,7 13 84 85

Mikä on todennäköisyys, että kahdella nopalla, lukuun ottamatta seiskaa, heitetään jokainen kokonaistulos vähintään kaksi kertaa ennen kuin tulokseksi tulee seiska?

Garrison

Tällaisten kysymysten juju on siinä, että todennäköisyys on sama, jos heittojen välinen aika noudattaa eksponentiaalista jakaumaa, jonka keskiarvo on 1. Tässä tapauksessa se voidaan antaa seuraavalla kaavalla.

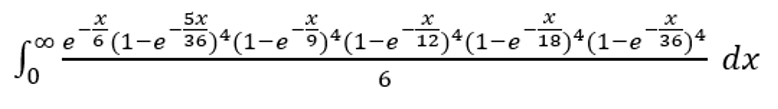
Tekstimuotoon laitetaan seuraava lauseke: exp(-x/6)*(1-exp(-5x/36))^4*(1-exp(-4x/36))^4*(1-exp(-3x/36))^4*(1-exp(-2x/36))^4*(1-exp(-1x/36))^4/6

Tällaisten integraalien ratkaisemiseen suosittelen tätä Integral Calculatoria .

Vastaus on 7864581698887803455719/10946915593544650625105200 =~ 0.0007184290069364848.