Kysy velholta #425

Q: <p>Tehtäväsi on leikata alla oleva kolmio kahteen yhtä suureen osaan yhdellä pystysuoralla leikkauksella (eli yhdensuuntaisesti a-sivun kanssa). Mihin leikkaus tulisi tehdä? </p><p></p><img alt="" height="354" src="/media/content_images/1610/ask-the-wizard-425-q.png" width="600" />

<div><button onclick='var btn = this; var div = btn.parentNode.childNodes[1]; if (div.style.display != "block") { div.style.display="block"; } else { div.style.display="none"; }' style='padding:2px 4px;'>Vastaus</button><div class='spoiler'> Leikkaus tulisi tehdä neliöjalan (b/sqrt(2)) kohdalta kolmion oikeasta reunasta. Huomaa, että korkeudella ei ole merkitystä. </div></div><p></p><p> Tässä on <a href="/pdf/2083/ask-the-wizard-425.pdf">ratkaisuni</a> (PDF).</p><p> Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani <a href="https://wizardofvegas.com/forum/questions-and-answers/math/34502-easy-math-puzzles/104/#post964901" target="_blank">Wizard of Vegasissa</a> .</p>

Q: <p><a href="wizardofodds.com/ask-the-wizard/424/">Kysy velholta -osiossa #424</a> joku kysyi: &quot;Yksimetrinen keppi leikataan kahdesta satunnaisesta kohdasta. Mikä on pienimmän luodun kolmesta palasta odotettu pinta-ala?&quot; Kysymykseni kuuluu, mikä olisi vastaus c satunnaisesta leikkauksesta?</p>

<div><button onclick='var btn = this; var div = btn.parentNode.childNodes[1]; if (div.style.display != "block") { div.style.display="block"; } else { div.style.display="none"; }' style='padding:2px 4px;'>Vastaus</button><div class='spoiler'>1/(c+1)^2</div></div><p></p><p> Tässä on <a href="/pdf/2082/ask-the-wizard-425b.pdf">ratkaisuni</a> (PDF).</p><p> Tätä ongelmaa on kysytty ja siitä on keskusteltu foorumillani <a href="https://wizardofvegas.com/forum/questions-and-answers/math/34502-easy-math-puzzles/104/" target=_blank>Wizard of Vegasissa</a> .</p>

Tehtäväsi on leikata alla oleva kolmio kahteen yhtä suureen osaan yhdellä pystysuoralla leikkauksella (eli yhdensuuntaisesti a-sivun kanssa). Mihin leikkaus tulisi tehdä?

anonyymi

Leikkaus tulisi tehdä neliöjalan (b/sqrt(2)) kohdalta kolmion oikeasta reunasta. Huomaa, että korkeudella ei ole merkitystä.

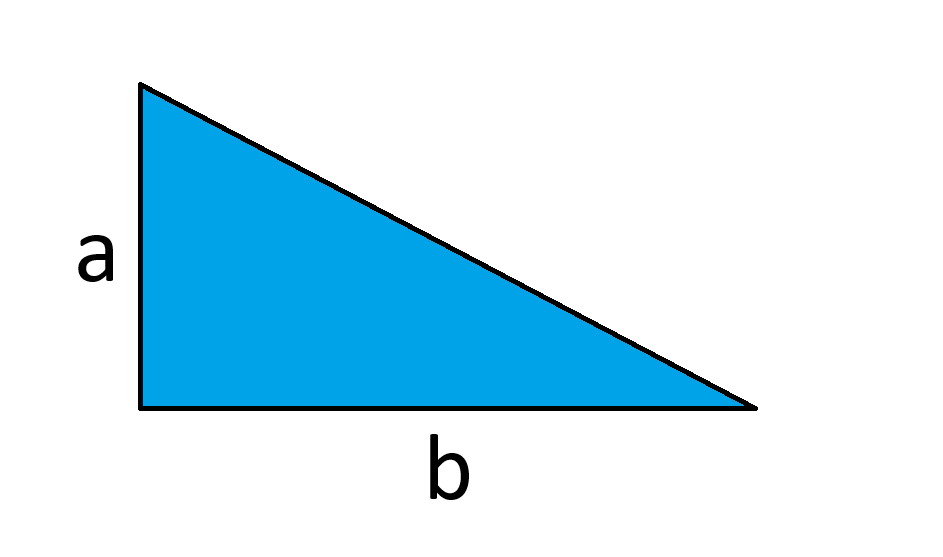
Tässä on ratkaisuni (PDF).

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Kysy velholta -osiossa #424 joku kysyi: "Yksimetrinen keppi leikataan kahdesta satunnaisesta kohdasta. Mikä on pienimmän luodun kolmesta palasta odotettu pinta-ala?" Kysymykseni kuuluu, mikä olisi vastaus c satunnaisesta leikkauksesta?

anonyymi

1/(c+1)^2

Tässä on ratkaisuni (PDF).

Tätä ongelmaa on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Kuinka monella tavalla voit sijoittaa kuusi erilaista palloa kolmeen samanlaiseen laatikkoon?

anonyymi

Vastaus on 122

Tämän tehtävän hankala puoli on se, että laatikot ovat identtisiä. Jos ne olisivat erilaisia, vastaus olisi helposti löydettävissä muodossa 3 ⁶ = 729.

Merkitään pallot A:sta F:ään. Aloitetaan asettamalla pallo A mihin tahansa laatikkoon.

Oletetaan ensin, että laitat pallon B toiseen jäljellä olevista kahdesta tyhjästä laatikosta. Tästä eteenpäin kolme laatikkoa ovat erilaisia, koska niissä on eri palloja, mukaan lukien yksi edelleen tyhjä. Muut neljä palloa voidaan sijoittaa 3 ⁴ = 81 eri tavalla.

Toiseksi, oletetaan, että laitat pallon B samaan laatikkoon kuin pallon A ja C yhteen tyhjistä laatikoista. Tästä eteenpäin kolme laatikkoa ovat erilaisia, koska niissä on eri palloja, mukaan lukien yksi edelleen tyhjä. Kolmen muun pallon sijoitustapoja on 3 ³ = 27.

Kolmanneksi, oletetaan, että laitat pallot B ja C samaan laatikkoon kuin pallot A ja D yhteen tyhjistä laatikoista. Tästä eteenpäin kolme laatikkoa ovat erilaisia, koska niissä on eri palloja, mukaan lukien yksi edelleen tyhjä. Kaksi muuta palloa voidaan sijoittaa 3 ² = 9.

Neljänneksi, oletetaan, että laitat pallot B, C ja D samaan laatikkoon kuin pallot A ja E yhteen tyhjistä laatikoista. Tästä eteenpäin kolme laatikkoa ovat erilaisia, koska niissä on eri palloja, mukaan lukien yksi edelleen tyhjä. Toisen pallon sijoittamistapa on 3 ^{* 1} = 3.

Viidenneksi, oletetaan, että laitat pallot B:stä E:hen samaan laatikkoon kuin pallot A:n ja F:n yhteen tyhjistä laatikoista. Palloja ei ole jäljellä, joten pallot AE voivat olla yhdessä laatikossa ja F toisessa.

Kuudenneksi ja viimeiseksi, kaikkiin saman laatikon palloihin on vain yksi tie.

Joten vastaus on 3 ⁴ + 3 ³ + 3 ² + 3 ¹ + 2 = 122.

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Mikä on jakajan keskimääräinen loppusumma blackjackissa olettaen, että jakaja ei saa blackjackia eikä häviä?

anonyymi