WOO logo

Velho suosittelee

Kysy velholta #427

Kakku jaetaan seuraavasti:

  • Ensimmäinen henkilö saa 1%
  • Toinen henkilö saa 2 % jäljellä olevasta osasta.
  • Kolmas henkilö saa 3 % jäljellä olevasta osasta.
  • Ja niin edelleen.

Kuka saa eniten kakkua? Taulukkolaskentaa tai raa'an voiman laskutoimituksia ei sallita.

anonyymi

Kymmenes henkilö saa eniten kakkua.

Tässä on ratkaisuni (PDF).

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Haluan antaa tunnustusta Mind Your Decisions -YouTube-kanavalle tästä matemaattisesta pulmasta.

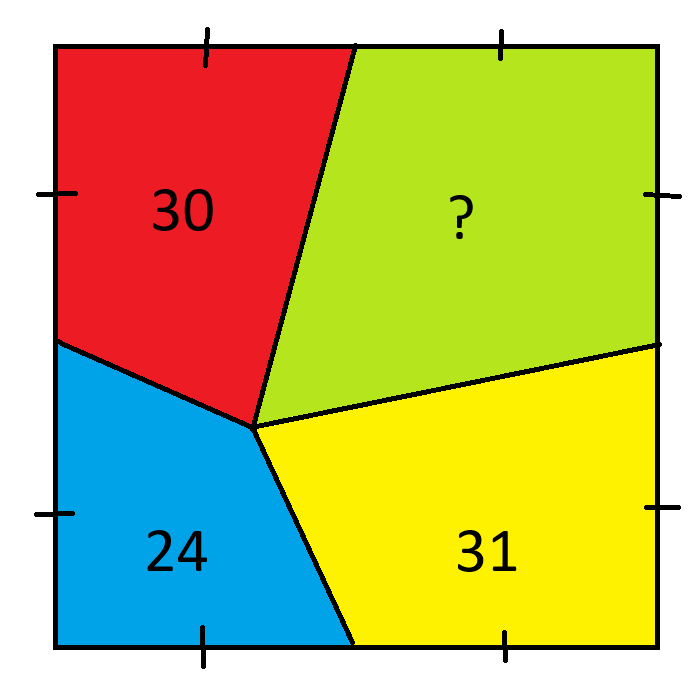
Mikä on vihreän alueen pinta-ala?

anonyymi

38

Piirrä ensin neljä viivaa neljän palan leikkauspisteestä jokaiseen kulmaan. Merkitse sitten kahdeksan palaa seuraavasti.

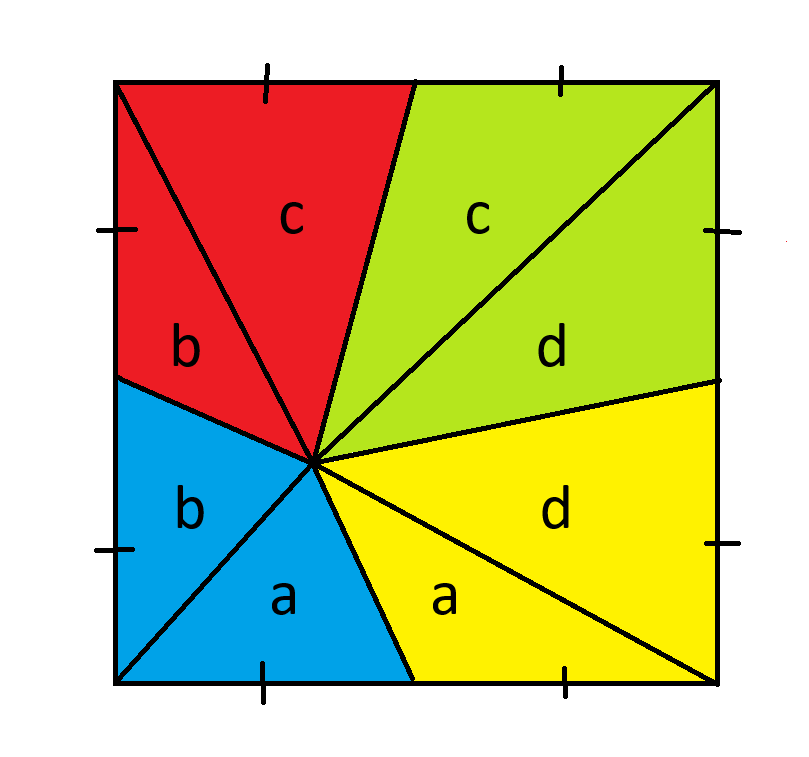
Muista, että kolmion pinta-ala on pohja * korkeus / 2. Koska kaikilla kolmioilla on sama pohja, voimme yhdistää samankorkuiset kolmiot samanpinta-alaisiksi.

Tässä vaiheessa tiedämme:

  • (1) A+B = 34
  • (2) B+C = 42
  • (3) A+D = 30

Yhtälöiden (2) ja (3) lisääminen:

A+B+C+D = 72

Vähennetäänpä tästä yhtälö (1):

C+D = 38, mikä on vastauksemme.

Tätä kysymystä esitettiin ja siitä keskusteltiin foorumillani Wizard of Vegasissa .

Pulman lähde on YouTube-video nimeltä "98% FAILED to Solve this Math Problem".

Oletetaan, että haluat löytää useiden arvojen keskiarvon. Mitä mieltä olet siitä, että poistettaisiin suurimmat ja pienimmät arvot, kuten tehdään voimistelun pisteytyksessä olympialaisissa? Oletetaan, että tarkoituksena on löytää tietyn naapuruston keskiarvo neliöjalkaa kohden.

anonyymi

Hyvä kysymys. Se, mistä puhut, on niin sanottu lyhennetty keskiarvo. Minulla ei ole tietoa lyhennetyn keskiarvon ja todellisen keskiarvon välisestä varianssista. Koska parempaa tietoa ei ollut, tein oman kokeeni.

Vastatakseni kysymykseesi otin 100 000 otosta kymmenestä arvojoukosta. Jokainen arvo jakautui standardinormaalijakauman mukaisesti, mikä tarkoittaa keskiarvoa 0 ja varianssia 1. Sitten tarkastelin kaikkien kymmenen arvon keskiarvoa sekä kahdeksan poisleikatun arvon keskiarvoa.

Havaitsin, että kaikkien kymmenen arvon otoskeskiarvon ja todellisen keskiarvon välinen keskimääräinen ero oli 0,003450. Saman menetelmän tekeminen, mutta trimmatun keskiarvon ottaminen, antoi eroksi keskimäärin 0,003445. Mielestäni tämä ei ole riittävän merkittävä ero, jotta voitaisiin päätellä, kumpi menetelmä on parempi. Lisäksi se, mikä saattaisi sopia kokeeseeni, ei välttämättä sovi toiseen sovellukseen.

Yhteenvetona totean, etten usein sano tätä, minulla ei ole lopullista matemaattista vastausta.

Mikä on tehokkaampi (eli vähiten tilaa hukkaava) tapa pinota palloja, joiden pohja on neliömäinen tai kolmiomainen?

anonyymi

Vastasin tähän kysymällä, millä pyramidilla oli suurin pallojen tilavuuden suhde niitä ympäröivän pyramidin tilavuuteen, kun pallojen lukumäärä lähestyi ääretöntä.

Ne ovat yhtä tehokkaita, hyötysuhteella 74,05 %.

Tässä on ratkaisuni (PDF).

Myöhemmin tajusin, että tämä kysymys oli esitetty myös Kysy velholta #350: ssä. Mielestäni tämä ratkaisu on kuitenkin parempi.