Todennäköisyys - Kortit
Pelasin baccaratia netissä ja 75 kädestä pankkiiri voitti 52 ja pelaaja 23. Ero on 29, mikä on todennäköisyys sille?
Ensinnäkin oletan, ettet laske tasapelejä. Toisin sanoen tarkoitat 75 ratkaistua vetoa. On hyvin epätodennäköistä, että 75 kättä päättyisi ilman tasapeliä. Pankkiirin voittojen odotusarvo 75 ratkaistusta vedosta on 38,00913745. Keskihajonta on luvun 75, pankkiirin voiton todennäköisyyden ja pelaajan voiton todennäköisyyden tulon neliöjuuri. Pankkiirin voiton todennäköisyys, olettaen, että tasapeliä ei ole, on 0,506788499 ja pelaajan voiton todennäköisyys on 0,493211501. Keskihajonta on siis 4,329727904. Sitten sinun on tehtävä puolen pisteen korjaus binomijakauman varalta ja etsittävä Z-tilasto tavallisesta normaalitaulukosta (tämä vaihe jätetään lukijan tehtäväksi). Lopullinen vastaus on, että todennäköisyys sille, että pankkiiri saa 52 tai enemmän voittoa, on 0,0009. Kysymyksessäsi otettiin huomioon myös se mahdollisuus, että pankkiiri voittaa 23 kertaa tai vähemmän (myös ero on 29 enemmän), minkä todennäköisyys on 0,0004. Joten lopullinen vastaus on, että 29:n tai suuremman eron todennäköisyys on 0,0013 eli 1/769.
Kun lasken pelaajan ja jakajan käsien yhdistelmiä Caribbean Stud Pokerissa , saan vain 3 986 646 103 440, kun taas sinun 19, jne. Olen virheellinen tasan kertoimella 5. Käytin kaavaa combin (52,5)*combin(47,5). Missä menin vikaan? Kiitos ja mielestäni sivustosi on yksinkertaisesti loistava.
Kiitos kehusta. Olet viisinkertaisesti väärässä, koska jakajalla voi olla mikä tahansa viidestä kortista kuvapuoli ylöspäin. Toisin sanoen järjestyksellä on merkitystä jakajan kädellä, koska ensimmäinen kortti jaetaan kuvapuoli ylöspäin. Kokonaisyhdistelmien oikea johtaminen on combin(52,5)*47*combin(46,4) = 19 933 230 517 200.
Mitkä ovat kertoimet saada kolme korttia pariin ja täyskäsi viiden kortin vetopokerissa?
Tässä tilanteessa on kaksi tapaa saada täyskäsi: (1) nostaa kolmoset tai (2) nostaa yksi lisää pariin ja toinen pari. Oletan, että hylkäät kolme yksittäistä kättä.
Lasketaan ensin yhdistelmien lukumäärä yhtälön (1) mukaisesti. Jäljellä on 3 arvoa ja vain 3 maata (muista hylätä 3 yksittäistä maata) ja 9 arvoa ja jäljellä on 4 maata. Yhdistelmien lukumäärä on siis 3*combin(3,3)+9*combin(4,3) = 3*1 + 9*4 = 39.
Lasketaan seuraavaksi kaavan (2) mukaisten yhdistelmien lukumäärä. Olemassa olevaan pariin on jäljellä 2 maata. On combin (3,2) tapaa muodostaa pari kolmesta maasta, kun jäljellä on 3 korttia, ja combin(4,2) tapaa muodostaa pari neljän kortin riveistä. Joten kaavan 2 mukaisten yhdistelmien kokonaismäärä on 2*(3*combin(3,2)+9*combin(4,2)) = 2*(3*3 + 9*6) = 126. Täyskäden muodostamisen tapojen kokonaismäärä on kaavojen (1) ja (2) summa eli 39+126=165. Toisella nostolla on combin(47,3)=16 215 tapaa järjestää kolme korttia. Täyskäden nostamisen todennäköisyys on täyskäden nostamistapojen lukumäärä jaettuna yhdistelmien kokonaismäärällä eli 165/16 215 = 0,0101758 eli noin 1/98.
Lisätietoja combin()-funktiosta on pokerin todennäköisyyksiä käsittelevällä osiollani.
Aloin pelata pokeria ystävieni kanssa kerran viikossa (viiden kortin veto, avopokeri, seitsemän kortin avopokeri). Pöydässä on seitsemän pelaajaa. Minusta tuntuu, että todennäköisyys saada oikeat kädet pienenisi dramaattisesti, koska kortit jaettaisiin useammalle pelaajalle 52 kortin pakasta. Onko sinulla matemaattista kaavaa, joka voisi ohjata minua oikeaan suuntaan?
Ei, minkä tahansa käden saamisen todennäköisyys on sama riippumatta siitä, kuinka monta muuta pelaajaa on pöydässä. Näkymätön kortti on näkymätön kortti, sillä ei ole väliä, onko se toisella pelaajalla vai onko se vielä pakassa.
Kuulin hiljattain tarinan, jota en voinut uskoa!! Eräs ystäväni kertoi minulle, että ystävällisessä pokeripelissä hänen kotonaan hän ja hänen ystävänsä saivat molemmat luonnollisen värisuoran samassa kädessä nostamatta kortteja!! (viiden kortin vedossa) Minun on vaikea uskoa tätä, ja sivustosi perusteella laskin yhden värisuoran todennäköisyydeksi noin 65 000 yhteen. Mikä olisi kahden suoran todennäköisyys yhdessä kädessä, kun pelissä on kuusi pelaajaa (ilman kortteja?)
Annan likimääräisen vastauksen olettaen, että jokaiselle pelaajalle jaettiin käsi omasta pakasta. Tämän ei pitäisi muuttaa todennäköisyyksiä juurikaan. Todennäköisyys sille, että yksi pelaaja saa värisuoran, kuten pokerin todennäköisyyksiä käsittelevässä osiossani on esitetty, on 36/2 598 960. Kutsutaan tätä todennäköisyyttä p:ksi. Kahden pelaajan todennäköisyys saada värisuora on yhdistettynä (6,2)* p² *(1-p) ⁴ = 0,0000000028779. Toisin sanoen, todennäköisyys sille, että tämä tapahtuu, on 347 477 740:1.
Miten lasket erilliset todennäköisyydet sille, että saat (1) kuningatarhain, (2) kuningashain ja (3) ässähain kolmen kortin pokerissa?
Lasken ensin kuningashain ja näytän lyhyesti kaavan kahdelle muulle. Todennäköisyys on kuningashain käsien lukumäärä jaettuna käsien kokonaismäärällä. Kuningasta pienempien käsien lukumäärä on 11. Kuningashain kädellä on oltava kaksi eri arvoista kättä. 2/11 -yhdistelmien järjestämistapojen lukumäärä on combin (11,2) = 55. Yksi näistä yhdistelmistä on kuitenkin kuningas-kuningatar-jätkä, mikä johtaa suoraan, joten vähentämällä tämä yhdistelmä jää jäljelle 54, jotka eivät muodosta suoraa. Seuraavaksi on neljä maata jokaista arvoa kohden eli 4 * 3 = 64 mahdollista maayhdistelmää. Näistä 64:stä neljä johtaa kuitenkin väriin, joten jäljellä on 64 - 4 = 60 maayhdistelmää. Joten kuningashain yhdistelmien kokonaismäärä on 54 * 60 = 3240. Yhteensä combin(52,3) = 22 100, jolloin saa järjestettyä 3 korttia 52:sta. Joten kuningashain todennäköisyys on 3 240 / 22 100 = 0,1466063. Ässähain todennäköisyys on: (combin(12,2)-2)*(4 3 -4) / combin(52,3) = 0,1737557. Huomaa -2 -1:n sijaan sekä a-2-3- että qka-suoran vuoksi.
Kuningattaren hai-arvon todennäköisyys on: (combin(10,2)-1)*(4 3 -4)/combin(52,3)=0.119457.
Mitkä ovat todennäköisyydet saada kuningasvärisuora? Saada peräkkäin kuningasvärisuora (eteen- tai taaksepäin)?
Minkä tahansa kuningasvärisuoran todennäköisyys on mahdollisten kuningasvärisuoran lukumäärä, joka on neljä (yksi kutakin maata kohden), jaettuna niiden tapojen lukumäärällä, joilla voi valita viisi korttia 52:sta, eli yhdistelmä (52,5) = 2 598 960. Vastaus on siis 4/2 598 960 = 0,00000153908 eli 1/649 740.
Peräkkäisen kuningasvärisuoran todennäköisyys on (maamäärä) * (suuntien lukumäärä) / (viiden kortin permutaatioiden kokonaismäärä 52:sta) = 4 * 2 / permut (52,5) = 8 / 311 875 200 = 8 / mahdollisten kuningasvärisuoran lukumäärä, joka on neljä (yksi kutakin maata kohden), kerrottuna mahdollisten suuntien lukumäärällä jaettuna tapojen lukumäärällä, joilla voi valita viisi korttia 52:sta, eli permut (52,5) = 311 875 200. Vastaus on siis 4/311 875 200 = 0,00000002565 eli 1/38 984 400.
Tykkään pelata valehtelijapokeria dollariseteleillä. Mikä on todennäköisyys saada setelille 1, 2, 3, 4 tai 5 samaa numeroa? Kiitos. Jos pelaan kolmen hengen pelissä, mikä on todennäköisyys sille, että yksi numero ilmestyy?
Ensin vastaan esittämättömään kysymykseen todennäköisyydestä, että tietty luku esiintyy n kertaa satunnaisella setelillä. Setelissä on 8 numeroa, joten tietyn luvun n todennäköisyys on combin(8,n)* 0.1n * 0.98-n / 108 . Tässä on taulukko, joka näyttää tietyn luvun todennäköisyyden sille, että se esiintyy 0-8.
Tarkat numerokertoimet Liar's Pokerissa
| Määrä | Todennäköisyys |
|---|---|
| 8 | 0.00000001 |
| 7 | 0.00000072 |
| 6 | 0.00002268 |
| 5 | 0.00040824 |
| 4 | 0.00459270 |
| 3 | 0.03306744 |
| 2 | 0.14880348 |
| 1 | 0.38263752 |
| 0 | 0.43046721 |
| Kokonais | 1.00000000 |
Seuraava taulukko näyttää kaikkien mahdollisten setelityyppien todennäköisyydet luokiteltuna kunkin n samanlaisen setelin lukumäärän mukaan. Esimerkiksi sarjanumerolla 66847680 olisi yksi kolmoset, yksi pari ja kolme yksittäistä seteliä, jolloin todennäköisyys olisi 0,1693440.
Yleiset todennäköisyydet valehtelijapokerissa
| 8 tammea | 7 tammea | 6 tammea | 5 tammea | 4 tammea | 3 tammea | 2 tammea | 1 tammi | Todennäköisyys |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0000001 | |||||||
| 1 | 1 | 0.0000072 | ||||||
| 1 | 1 | 0.0000252 | ||||||
| 1 | 2 | 0.0002016 | ||||||
| 1 | 1 | 0.0000504 | ||||||
| 1 | 1 | 1 | 0.0012096 | |||||
| 1 | 3 | 0.0028224 | ||||||
| 2 | 0.0000315 | |||||||
| 1 | 1 | 1 | 0.0020160 | |||||
| 1 | 2 | 0.0015120 | ||||||
| 1 | 1 | 2 | 0.0211680 | |||||
| 1 | 4 | 0.0211680 | ||||||
| 2 | 1 | 0.0020160 | ||||||
| 2 | 2 | 0.0141120 | ||||||
| 1 | 2 | 1 | 0,0423360 | |||||
| 1 | 1 | 3 | 0.1693440 | |||||
| 1 | 5 | 0.0846720 | ||||||
| 4 | 0,0052920 | |||||||
| 3 | 2 | 0.1270080 | ||||||
| 2 | 4 | 0,3175200 | ||||||
| 1 | 6 | 0.1693440 | ||||||
| 8 | 0.0181440 | |||||||
| Kokonais | 1.0000000 | |||||||
tammi = "eräänlainen"
Lisätietoja on valehtelijapokeria käsittelevällä sivullani.
Mitkä ovat jätkäparin saamisen todennäköisyydet 52 kortin pakalla?
Olettaen, että nostat viisi korttia ja lasket kaikki kädet, joissa on tasan kaksi jätkää, todennäköisyys olisi combin(4,2)*combin(48,3)/combin(52,5) = 6*17296/2598960 = 3,99%.
Mikä on todennäköisyys saada kolmospari Pai Gow -pokerissa? Ovatko mahdollisuudet pienemmät vai suuremmat kuin kolmoset?
Kolmosia ja kahta paria lukuun ottamatta seuraavat tavat saada kolmospari ja yhdistelmien lukumäärä.
Ei jokerikorttia: combin(13,3)*10*6 3 *4 =2471040
Ässäparin kilpailussa käytetty villi kortti: combin(12,2)*10*6 2 *4 2 = 380 160
Villikorttia käytetään singleton-ässänä: combin(12,3)*6 3 = 47 520
Yhdistelmien kokonaismäärä on 2 898 720. Tämä on alle puolet kolmosten 747 0676 yhdistelmästä.
Kaavasi mukainen todennäköisyys kuningasvärisuoralle on 4/2 598 960 = 1/649 740. Jos siis pelaisin Caribbean Studia jakajan kanssa yksi vastaan yksi, käteni ja jakajan käteni olisivat 649 740 * 2 = 1 299 480. Näin ollen matematiikan mukaan 1 299 480 käden jälkeen pitäisi olla kaksi kuningasvärisuoraa. Kerrothan minulle, ymmärränkö todennäköisyydet oikein.
Olet oikeassa siinä, että keskimäärin kuningasvärisuora muodostuu kerran 649 740 kädestä ja että 1 299 480 kädessä kuningasvärisuoran odotettu määrä on 2. Tämä on kuitenkin vain keskiarvo. Et ole lähempänä kuningasvärisuoran saamista jokaisella kädellä. Jokaisella itsenäisesti pelatulla pelillä on tämä muistiton ominaisuus, joten kuningasvärisuora ei ole koskaan myöhässä.
Todennäköisyys sille, että 1 299 480 kädessä ei ole yhtään kuninkaallista, on 13,53 %.
Hei, olen Pai Gow -pokerin vakiopelaaja ja huomasin sivustollanne paljon hyvää tietoa pelistä. Eräänä päivänä, kun pelasin ystäväni kanssa, hänelle jaettiin käsi, jonka korko on 9, mikä on mielestäni pienin mahdollinen käsi. Koko pelin parissa viettämäni ajan aikana minulle oli tapahtunut vain kerran aiemmin. Sitten viisi kättä myöhemmin hän sai täsmälleen saman käden (2-3-4-5-7-8-9). Emme voineet uskoa sitä ja mietimme, mitkä ovat sen todennäköisyydet, joten ajattelimme kysyä teiltä. Kiitos ajastanne ja upeasta sivustostanne.
On kaksi tapaa järjestää kortit 9-korkean käden muodostamiseksi: mainitsemasi ja 2-3-4-6-7-8-9. Maayhdistelmien lukumäärä ilman värin muodostumista on 4 7 -4*(combin(7,5)*3^2+6*3+1) = 15 552. Joten 9-korkean käden todennäköisyys on 2*15 552/combin(53,7) = 31 104/154 143 080 eli 1/9 911. Jos pelaisit vain viisi kertaa, todennäköisyys saada kaksi 9-korkeaa kättä olisi 1/9 826 685. Uskon, että tämä tapahtui sattumaa, toisin kuin satunnaislukugeneraattorin tai ohjelman koodauksen vika.
Kysymykseni liittyy talon etuun ja riskitekijöiden laskelmiin Casino Warissa Casino Niagaran säännöissä (eli 3-1 voitto korotukselle ja alkuperäisen panoksen häviämiselle). Miten keksit nämä luvut, joita yritän parhaillaan laskea? Minulla on vaikeuksia. Kiitos avustasi.
Olkoon d pakkojen lukumäärä. Tasapelin todennäköisyys ensimmäisellä kierroksella on (4*d-1)/(52*d-1) = 0,073955. Tasapelin todennäköisyys toisella kierroksella on 12*4*d/(52*d-2)*(4*d-1)/(52*d-3)+(4*d-2)/(52*d-2)*(4*d-3)/(52*d-3) = 0,073974. Kutsutaan p 1 tasapelin todennäköisyydeksi ensimmäisellä kierroksella ja p 2 tasapelin todennäköisyydeksi toisella kierroksella. Tällöin pelaajan palautus on p 1 *(2*p 2 +(1-p 2 )/2*(1-2))= -0,023301. Kerro tämä -1:llä, niin talon etu on 2,33 %. Toivottavasti en käynyt tätä läpi liian nopeasti.
Voisitko kertoa minulle, miten Karibian yhdistelmien kokonaismäärään, 19 933 230 517 200, päädyttiin? Seurasin viiden kortin pokeriyhdistelmiäsi ja sain tulokseksi 2 598 960. Miten jatkan siitä eteenpäin? Kiitos etukäteen.
Laskit oikein pelaajayhdistelmien määrän seuraavasti: comb (52,5)=2 598 960. Tästä eteenpäin jakajalla voi olla comb(47,5)=1 533 939 mahdollista kättä. Sitten mikä tahansa viidestä jakajan kortista voi olla kuvapuoli ylöspäin. Joten 2 598 960 * 1 533 959 * 5 = 19 933 230 517 200.
Ensinnäkin haluan sanoa, että mielestäni verkkosivustosi on todella mahtava. Olen kertonut siitä muutamille ihmisille ja toivon, että hekin kokeilevat sitä. Toivotan sinulle jatkuvaa menestystä sen kanssa. Pidin myös linkistä WinPokeriin. Pidin WinPokerista niin paljon, että tilasin sen. Tämä on loistava ohjelma. Minulla on kysymys, johon toivon, että voit auttaa minua. Olen yrittänyt selvittää, kuinka monta kertaa kukin käsi esiintyy seitsemän kortin studissa. Minulla on kopio seitsemän kortin pöydästäsi , mutta olen kiinnostunut matematiikasta, jolla näihin lukuihin päädytään. Pystyn selvittämään viiden kortin numerot, mutta seitsemän kortti vain hämmentää minua. Haluaisin lähettää Excel 2000 -tiedoston, jossa on numeroni. Haluaisin myös tietää, miten lasketaan suorien lukumäärä 53 kortin pakassa, jossa on jokeri. APUA! ! !
Kiitos ystävällisistä sanoistasi. Olen samaa mieltä siitä, että seitsemän kortin studin numeroiden laskeminen on vaikeaa. Siksi teen sen tietokoneella. Ohjelmani käy läpi kaikki mahdolliset yhdistelmät ja laskee jokaisen. Pai Gow -pokerissa villien suorien määrä on 11 * (4 4 -4) + 10 * 3 * (4 4 -4) = 10332. Yhdessä 10200 luonnollisen suoran kanssa kokonaismäärä on 20532.
Ymmärrän, mitkä ovat todennäköisyydet saada kuninkaallinen värisuora kenellä tahansa Caribbean Stud Poker- tai Let it Ride -pöydässä ja miten ne johdetaan. Mutta kysymykseni kuuluu: mitkä ovat peliä kolmannen osapuolen näkökulmasta näkemisen todennäköisyydet nähdä jonkin näistä käsistä jaettavan pelaajalle pöydässä millä tahansa jaolla? Uskon, että se riippuu pelattavien käsien lukumäärästä... onko kyse vain yksilön todennäköisyydestä kerrottuna pelattavien käsien lukumäärällä. Eli kuninkaallisen värisuoran näkeminen millä tahansa kädellä, kun pöydässä on neljä pelaajaa, tarkoittaa 4* todennäköisyyttä saada kuninkaallinen? Olen hieman hämmentynyt!
Menetelmäsi on hyvä approksimaatio. Tuon logiikan mukaan kolikkoa heitettäessä todennäköisyys sille, että ainakin yksi kolmesta heittää kruunan, olisi 3 * 50 % = 150 %. Olettaen riippumattomat tapahtumat, ainakin yhden onnistumisen todennäköisyys n yrityksestä, joissa jokaisen onnistumisen todennäköisyys on p, on 1-(1-p) n . Kolikonheittoesimerkissä tämä olisi 1-0,5 * 3 = 0,875. Neljän Caribbean Stud Pokerin pelaajan tapauksessa ainakin yhden kuningasvärisuoran todennäköisyys olisi 1-(1-4/2598960) 4 = 0,00000615629. Koska kaikki kortit jaetaan samasta pakasta, tapahtumat eivät ole riippumattomia. Matematiikka on erittäin monimutkaista tarkalleen oikean vastauksen määrittämiseksi, ja approksimaation pitäisi olla hyvin lähellä oikeaa vastausta.
Mikä on todennäköisyys saada luonnollinen seitsemän kortin värisuora Pai Gow -pokerissa? Työskentelen kasinolla ja näin tämän juuri ensimmäistä kertaa 15 vuoteen. Onnekas asiakas voitti 40 000 dollaria.
Luonnollisia värisuoria on 32 mahdollista (4 arvoa kertaa 8 mahdollista seitsemän kortin jakoa). 53 kortin yhdistelmällä 7 korttia voidaan nostaa 1 541 430 80 mahdollista tapaa. Vastaus on siis 32/1 541 430 80 eli 1/481 6971.
Mikä on todennäköisyys saada kaksi identtistä värisuoraa (sekä arvossa että maassa) kahdessa kädessä peräkkäin Three Card Pokerissa?
Todennäköisyys saada värisuora ensimmäisellä kädellä on 4 * 12 / combin(52,3) = 48/22100 = ~ 0,0022. Todennäköisyys sille, että seuraava käsi on täsmälleen sama, on 1/22100. Joten vastaus on (48/22100) * (1/22100) = 48/488410000, todennäköisyys 1/10 175 208. Tämä on 1,37 kertaa todennäköisempi kuin 6/49-lottovoiton saaminen, jonka todennäköisyys on 1/1 3983 816.
Mikä on todennäköisyys saada sekä pelaajalle että pankkiirille ässä ja ruutukaksi samassa jaossa 8-pakan baccaratissa?
(8 2 /yhdistelmä(416,2))* (7 2 /yhdistelmä(414,2)) = 0,00000043 tai 1:2308093
Näin hiljattain oudon tapahtuman. Katsoin viiden kortin vetopokeria, jossa sai nostaa enintään kaksi korttia. Yksi pelaaja nosti yhden kortin ja sai herttaväriuuhun. Jakaja nosti yhden kortin ja nosti pataväriuuhun. Luonnollisesti jakajan väri oli korkeampi. Pelissä oli mukana kolme muuta pelaajaa. Mitkä ovat todennäköisyydet saada kaksi väriä samassa kädessä?
Määritellään todennäköisyys, että pelaaja saa joko värin jakamisen yhteydessä tai saa neljän kortin värin. Yksinkertaisuuden vuoksi oletamme, että pelaaja saa tasaparin tai suoran, jossa on neloset ja väri. Värin saamisen todennäköisyys jakamisen yhteydessä (suoraa/kuningasvärisuoraa lukuun ottamatta) on 4*(combin(13,5)-10)/combin(52,5) = 5108/2598960 = 0,0019654. Neljän kortin värin saamisen todennäköisyys on 4*3*combin(13,4)*13/combin(52,5) = 111540/2598960 = 0,0429172. Värin täydentämisen todennäköisyys noston yhteydessä on 9/47. Kokonaistodennäköisyys saada neljän kortin väri ja täydentää se on siis 0,0429172 * (9/47) = 0,0082182. Värin kokonaistodennäköisyys on siis 0,0019654 + 0,0082182 = 0,0101836. Todennäköisyys sille, että tasan 2/5 pelaajaa saa värin, on combin(5,2) * 0,0101836 2 * (1-00,0101836) 3 = 0,001006 eli noin 1/994.
Haluaisin tietää, mikä on todennäköisyys sille, että joku saa neloset 7 Card Stud -kädessä, jossa on viisi pelaajaa ja yksi korttipakka? Toivottavasti voit auttaa minua ja kiitos ajastasi.
On olemassa combin(52,7) = 133 784 560 tapaa järjestää 7 korttia 52:sta. Neloset sisältävien 7 kortin sarjojen lukumäärä on 13 * combin(48,3) = 224 848. Luku 13 on nelosten sijoitusten lukumäärä ja combin(48,3) on tapojen lukumäärä, joilla voit valita 3 korttia jäljellä olevista 48 kortista. Todennäköisyys on siis 224 848 / 133 784 560 = 0,0017 eli 1/595.
Kun avaat uuden korttipakan, ne antavat kummastakin maasta ässän ja kuninkaan. Mikä on todennäköisyys ottaa sekoitettu korttipakka ja sekoittaa se uudelleen alkuperäiseen ässästä kuninkaaksi -tilaansa?
1/52 kertoma eli 1/80 658 175 170 943 900 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000.
Jos kymmenelle pelaajalle jaetaan kullekin kaksi korttia yhdestä pakasta, mikä on todennäköisyys, että kahdella pelaajalla on ässäpari?
Ensinnäkin on 10 * 9/2 = 45 tapaa valita kaksi pelaajaa 10:stä. Todennäköisyys sille, että kaksi pelaajaa saa neljä ässää, on 1/combin(52,4) = 1/270725. Joten todennäköisyys sille, että kaksi pelaajaa saa ässäparin, on 45/270725 = 0,0001662.
Jos seitsemän pelaajaa saa kukin seitsemän korttia, mikä on todennäköisyys, että ainakin yksi saa seitsemän kortin värin?
Todennäköisyys sille, että yksi pelaaja saa seitsemän kortin värin, on 4 * combin(13,7) / combin(52,7) = 1/19491. Todennäköisyys sille, että ainakin yksi seitsemästä pelaajasta saa seitsemän kortin värin, on noin 1/2785.
Tiedän, että matemaattisesti kaikki on mahdollista, mutta eräänä iltana kasinolla luulin nähneeni jotain, jossa kertoimet olisivat miljardi yhteen, vaikka sellaisia ei koskaan tapahtuisikaan. Tässä on mitä tapahtui: Let it Ride -pöydässä jaettiin 40 käden aikana (40 yksittäistä kolmen kortin jakoa noin 8 kierrosta 5 pelaajalla) kolme nelosta. Kun nelosten kertoimet ovat noin 4100 yhteen, mikä olisi todennäköisyys sille, että neloset jaettaisiin kolme 40 jaon aikana? Ole hyvä ja vastaa, sillä tämä tappaa minut. Olen ollut pitkään fani.
Yksinkertaisuuden vuoksi oletetaan, että jokainen käsi jaetaan uudesta pakasta. Nelosten todennäköisyys on 13 * 48 / combin(52,5) = 624 / 2598960. Todennäköisyys sille, että nelosia on tasan 3/40, on combin(40,3) * p 3 * (1-p) 37 = 1/7378135, missä p = 624 / 2598960. Eli se on enemmänkin kuin 1/7 miljoonan lyönti.
Ensin halusin kertoa, kuinka paljon seuraan ja rakastan verkkosivustoasi ja ihailen matemaattisia taitojasi. Käytän blackjackin jakamiseen kuutta pakkaa ja lisäsin kolme jokeria syistä, joihin en aio tuhlata aikaasi, mutta mitkä ovat todennäköisyydet jakaa kaikki kolme jokeria pelaajalle peräkkäin? Kiitos paljon.
Ole hyvä, kiitos kohteliaisuuksistasi. Todennäköisyys saada kolme jokeria peräkkäin kuuden pakan kengästä (plus kolme jokeria) on 1/combin(315,3) = 1/5 159 805. Toinen ratkaisu on (3/315)*(2/314)*(1/313).
Mitkä ovat todennäköisyydet sille, että 52 kortin pakalla jaetaan 13 korttia neljälle pelaajalle kullekin ja kaikilla neljällä pelaajalla on suora ässästä kakkoseen? Korttien ei tarvitse olla samaa maata.
Vastaus on (4 13 /KOMBIN(52,13))* (3 13 /KOMBIN(39,13))* (2 13 /KOMBIN(26,13)) = 1 luvusta 61 204 166 001.
Mikä on todennäköisyys sille, että kuninkaalliselle pelaajalle jaetaan neljä?
Kuningaskortille on neljä mahdollista maata. Viisi mahdollista puuttuvaa korttia on myös. Viides kortti voi olla yksi 47 muusta kortista. Joten on 4 * 5 * 47 = 940 tapaa saada neljä kuningaskorttia. Yhdistelyjä on yhteensä (52,5) = 2 598 960. Todennäköisyys on siis 940/2 598 960 = 1/2 765.
Hyvä velho, oletetaan, että sekoitetaan 52 kortin pakka ja nostetaan satunnaisesti 18 korttia 52:sta ja jaetaan 18 korttia kuuteen kolmen kortin pinoon. Mikä on todennäköisyys, että yhdessä pinoista on täsmälleen 3 (neljästä) ässää?
Helpoin tapa ratkaista ongelma on, että todennäköisyys sille, että ensimmäisessä pinossa on kolme ässää, on (4/52)*(3/51)*(2/50) = 1/5525. Jokaisella pinolla on kuitenkin yhtä suuri todennäköisyys saada kolme ässää, joten kerromme sen 6:lla, jolloin saadaan 6/5525 = 0,001086.
Mikä on todennäköisyys saada kaikki kuvakortit Five Card Studissa?
(12/52)*(11/51)*(10/50)*(9/49)*(8/48) = 0,00030474 eli noin 1/3282.
Mikä on todennäköisyys saada kaksi nelosta kahden tunnin aikana pelattaessa Let it Ride -peliä?
Nelosten todennäköisyys missä tahansa kädessä on 13 * 48 / combin(52,5) = 0,0002401. Oletetaan, että kahdessa tunnissa voit pelata 120 kättä. Tasan kahden nelosen todennäköisyys olisi combin(120,2) × 0,0002401 2 × (1 - 0,0002401) 118 = 0,000400095 = 1/2499,41.
Neljän kortin pokerissa, kumpi on todennäköisemmin suora vai väri?
Jos värisuoria ja kuningasväriuistimia ei lasketa mukaan, suoran todennäköisyys on 1,02 % ja värin todennäköisyys 1,04 %. Värin todennäköisyys on siis hieman suurempi.
Mikä on todennäköisyys sille, että miljoonan käden aikana tulee 200 000 käden mittainen kuningasvärisuoran kuivuus? Olen kiinnostuneempi ratkaisusta kuin itse vastauksesta.
En sano tätä usein, mutta yritin tuntikausia, mutta tämän matematiikan ymmärtäminen oli minulle yksinkertaisesti liian vaikeaa. Niinpä käännyin ystäväni ja matematiikan professorini Gabor Megyesin puoleen. Tässä on hänen kaavansa mille tahansa "kuivuus"-ongelmalle.
- Olkoon p minkä tahansa käden voittamisen todennäköisyys.
- Olkoon d kuivuuden pituus.
- Olkoon n pelattujen käsien lukumäärä.
- Aseta k=dp ja x=np.
- Jos k=1, olkoon a=-1, muuten etsi sellainen a, että k=-ln(-a)/(1+a). (a on negatiivinen luku, jos k>1, niin -1 < a < 0, jos k < 1, niin a < -1, ja a on laskettava suurella tarkkuudella.) [Ohjatun toiminnon huomautus: Tällainen ratkaisu löytyy helposti Excelistä käyttämällä työkalut-valikon tavoitteen haku -toimintoa.]
- jos k=1, niin olkoon A=2, muuten olkoon A=(1+a)/(1+ak).
- Todennäköisyys sille, ettei n kädessä ole d-pituista kuivuutta, on noin Ae a x .
Tässä nimenomaisessa ongelmassa p=1/40391, d=200000, n=1000000, k=4,9516, x=24,758, a=-0,0073337, A=1,03007. Joten kuivuuden puuttumisen todennäköisyys on 1,03007*e -0,0073337*24,758 = 0,859042. Näin ollen ainakin yhden kuivuuden todennäköisyys on 1-0,859042 = 0,140958.
Tässä on Gabor Megyesin täydellinen viisisivuinen ratkaisu (PDF). Kiitos Gábor avustasi.
Tein satunnaisen simulaation 32 095 miljoonan käden sarjasta. Määrä, jossa oli ainakin yksi "kuivuus", oli 4558, todennäköisyydellä 14,20 %.
Oletetaan, että sinulla on kaksi viiden kortin pokerikättä erillisistä pakasta. Sinulle kerrotaan, että kädessä A on ainakin yksi ässä. Sinulle kerrotaan, että kädessä B on pataässä. Kummassa kädessä on todennäköisemmin ainakin yksi ässä enemmän?
Seuraava taulukko näyttää 0–4 ässän todennäköisyyden täysin satunnaisessa kädessä.
Ässätodennäköisyydet — Satunnainen käsi
| Ässät | Kaava | Yhdistelmät | Todennäköisyys |
|---|---|---|---|
| 0 | yhdistelmä(48,5) | 1712304 | 0,658842 |
| 1 | yhdistelmä(4,1) × yhdistelmä(48,4) | 778320 | 0.299474 |
| 2 | yhdistelmä(4,2) × yhdistelmä(48,3) | 103776 | 0,03993 |
| 3 | yhdistelmä(4,3) × yhdistelmä(48,2) | 4512 | 0,001736 |
| 4 | yhdistelmä(4,4) × yhdistelmä(48,1) | 48 | 0.000018 |
| Kokonais | 2598960 | 1 |
Laske yhteen 1–4 ässää, niin näemme, että ainakin yhden ässän todennäköisyys on 0,341158. Kahden tai useamman ässän todennäköisyys on 0,041684.
Todennäköisyys sille, että ässäjä on ainakin yksi lisää, olettaen, että ässäjä on ainakin yksi, voidaan Bayesin lauseen mukaisesti muotoilla seuraavasti: todennäköisyys (kaksi ässää lisää, kun otetaan huomioon ainakin yksi ässä) = todennäköisyys (kaksi tai useampi ässä) / todennäköisyys (ainakin yksi ässä) = 0,041684 / 0,341158 = 0,122185.
Niille, jotka ovat ruosteessa Bayesin lauseen kanssa, se toteaa, että A:n todennäköisyys tietyllä B:llä on yhtä suuri kuin A:n ja B:n todennäköisyydet jaettuna B:n todennäköisyydellä, eli Pr(A tietyllä B:llä) = Pr(A ja B)/Pr(B).
Seuraava taulukko näyttää muiden ässänumeroiden yhdistelmät ja todennäköisyydet, kun pataässä on poistettu pakasta.
Ässätodennäköisyydet — Ässä poistettu käsi
| Ässät | Kaava | Yhdistelmät | Todennäköisyys |
|---|---|---|---|
| 0 | yhdistelmä(3,0) × yhdistelmä(48,4) | 194580 | 0,778631 |
| 1 | yhdistelmä(3,1) × yhdistelmä(48,3) | 51888 | 0,207635 |
| 2 | yhdistelmä(3,2) × yhdistelmä(48,2) | 3384 | 0,013541 |
| 3 | yhdistelmä(3,3) × yhdistelmä(48,1) | 48 | 0,000192 |
| Kokonais | 249900 | 1 |
Tämä osoittaa, että ainakin yhden lisäässän todennäköisyys on 0,221369.
Hauskuuden vuoksi ratkaistaan sama tehtävä Bayesin lauseen avulla. Oletetaan, että jaetaan satunnaisia käsiä, kunnes yksi sisältää pataässän. Todennäköisyys sille, että kädessä on pataässä, tulee ainakin yksi lisäässä, voidaan kirjoittaa uudelleen muotoon todennäköisyys (ainakin kaksi ässää, kun kädessä on pataässä). Bayesin lauseen mukaan tämä on yhtä kuin Todennäköisyys (kädessä on pataässä ja ainakin yksi ässä lisää) / Todennäköisyys (kädessä on pataässä). Voimme jakaa osoittajan muotoon Todennäköisyys (2 ässää pataässä mukaan lukien) + Todennäköisyys (3 ässää pataässä mukaan lukien) + Todennäköisyys (4 ässää). Ensimmäisen taulukon perusteella tämä on yhtä kuin 0,039930 × (2/4) + 0,001736 × (3/4) + 0,000018 = 0,021285. Pataässän todennäköisyys on 5/52 = 0,096154. Joten ainakin kahden ässän todennäköisyys, kun otetaan huomioon pataässät, on 0,021285 / 0,096154 = 0,221369.
Joten kahden tai useamman ässän todennäköisyys, jos mukana on ainakin yksi ässä, on 12,22 % ja pataässä, jos mukana on 22,14 %.
Okei, uskon lukuihisi, mutta ne eivät vieläkään ole minusta järkeviä. Luulisin, että todennäköisyydet olisivat samat. Mitä merkitystä maalla on sille yhdelle ässälle, jonka sait?
Tarkastellaan toista yksinkertaisempaa tilannetta. Oletetaan, että nainen A sanoo: "Minulla on kaksi lasta ja ainakin toinen on poika." Nainen B sanoo: "Minulla on kaksi lasta ja vanhempi on nimeltään John." Voimme olettaa, että kukaan John-niminen lapsi ei ole tyttö eikä kukaan nainen anna samaa nimeä useammalle kuin yhdelle lapselle. Käyttämällä ehdollista todennäköisyyttä todennäköisyys sille, että molemmat lapset ovat naisen A poikia, on pr(molemmat pojat)/pr(ainakin yksi poika) = pr(molemmat pojat)/(1 - pr(molemmat tytöt)) = (1/4)/(1-(1/4)) = (1/4)/(3/4) = 1/3. Naisen B nuoremman lapsen todennäköisyys sille, että se on poika tai molemmat lapset ovat poikia, on kuitenkin ?, koska vanhemman lapsen nimeksi nimeäminen John ei kerro meille mitään nuoremmasta lapsesta.
Toisena esimerkkinä oletetaan, että menet Jiffy Lubeen ja he tarjoavat kaksi tarjousta samaan hintaan. Tarjous A:ssa he tarkistavat neljä osaa ja vaihtavat vain ensimmäisen löydetyn viallisen. Tarjous B:ssä he tarkistavat vain yhden ongelman ja korjaavat sen, jos sellainen löytyy. Eikö olisikin parempi valita tarjous A? Autossasi oli sama määrä odotettuja viallisia osia, mutta ongelman löytämisen todennäköisyys on suurempi tarjouksella A, joten lähdet pois pienellä määrällä odotettuja viallisia osia kyseisen sopimuksen mukaisesti. Samoin minkä tahansa ässän testi todennäköisesti paljastaa ainoan ässän, kun taas pataässän testi ei tarkista kolmea muuta maata, joten ne ovat todennäköisemmin ässät.
Miten päädyit värisuorien lukumäärään 2072, kun neljällä kortilla viidestä on neljän kortin pokerissa?
Ensin jaottelin värisuorat kahteen tyyppiin: neljän peräkkäisen saman maan kortin värisuorat ja viiden saman maan kortin värisuorat. Viiden kortin värisuorien lukumäärä on maamäärä * välien lukumäärä (ässästä 10:een pienimpänä korttina) = 4 * 10 = 40. Neljän kortin värisuorissa on 11 erilaista väliä (ässästä jätkään pienimpänä korttina). A234- ja JQKA-värisuorissa viides kortti voi olla yksi 47:stä (52 vähennettynä neljällä jo poistetulla kortilla ja viides kortti, joka muodostaisi viiden kortin värisuoran, jotka oli jo laskettu mukaan). Joten A234- tai JQKA-välin värisuoria on 4 * 2 * 47 = 376. Muista yhdeksästä on 46 mahdollista korttia viidennelle kortille (52 vähennettynä neljällä jo poistetulla kortilla ja kaksi kortille, jotka muodostaisivat viiden kortin värisuoran). Joten välin 2345 ja TJQK välisten värisuorien lukumäärä on 4 * 9 * 46 = 1656. Joten neljän kortin värisuorien kokonaismäärä on 40 + 376 + 1656 = 2072.
Väri on 100 % mahdollinen 17. jaetulla kortilla riippumatta siitä, mitä tapahtuu. Milloin suora on 100 % mahdollinen milläkin jaetulla kortilla?
Suora on taattu vain 45 kortilla. Voit esimerkiksi jakaa kaikki kortit A, 2, 3, 4, 6, 7, 8, 9, JQ ja K, yhteensä 44 korttia, eikä sinulla silti ole suoraa.
Rakas mahtava herra Kertoimien Velho, olen täysin ja ällistynyt tilastollisesta tarkkanäköisyydestäsi. Voisitko sattumalta laskea minulle seitsemän kortin suoran todennäköisyyden - eli ässä, 2, 3, 4, 5, 6, 7 tai 2, 3, 4, 5, 6, 7, 8 tai 7, 8, 9, 10, jätkä, kuningatar, kuningas Seven Card Studissa? Ymmärrämme, että tämä ei ole oikea pokerikäsi; se kuitenkin tuli esiin pelatessamme ja mietimme, oliko sen todennäköisyys pienempi kuin normaalilla täyskädellä Seven Card Studissa. Kiitos, oi tietäväinen.
Kuinka voin kieltäytyä, kun olet hemmotellut minua noin hienosti? Ensinnäkin on olemassa yhdistelmä (52,7) = 133 784 560 tapaa valita 7 korttia 52:sta järjestyksestä riippumatta. 7 kortin suoralle on 8 mahdollista väliä (alin kortti voisi olla A:sta 8:aan). Jos meillä olisi 7 eri arvoa, on 4 7 = 16 384 tapaa järjestää maat. Huomaa, että tämä sisältää kaikki saman maan kortit, jotka muodostavat värisuoran. Todennäköisyys on siis 8 * 16 384 / 133 784 560 = 1/1020,6952.
Jos jaan yhdestä pakasta neljä korttia, mikä on todennäköisyys sille, että ainakin yksi kortti on pata?
Nollan patanumeron todennäköisyys on (39/52)*(38/51)*(37/50)*(36/49) = 0,303818. Joten ainakin yhden patanumeron todennäköisyys on 1-0,303818 = 0,696182.
Yhden pakan pelissä, mikä on todennäköisyys saada ainakin yksi ässä ja kakkonen neljästä kortista? Tämä on hyödyllistä tietää Omahaa pelatessa.
Todennäköisyydestä 101 tiedämme Pr(A tai B) = Pr(A) + Pr(B) - Pr(A ja B). Joten Pr(A ja B) = Pr(A) + Pr(B) - Pr(A tai B). Oletetaan, että A saa ässän ja B kakkosen. Pr(A) = Pr(ainakin yksi ässä) = 1 - Pr(ei ässää) = 1 - combin(48,4) / combin (52,4) = 1 - 0,7187 = 0,2813. Todennäköisyys sille, ettei kakkosia tule, olisi ilmeisesti sama. Samalla logiikalla pr(A tai B) = Pr(ainakin yksi ässä tai kakkonen) = 1 - Pr(ei ässää eikä kakkosta) = 1 - combin(44,4) / combin(52,4) = 1 - 0,501435 = 0,498565. Joten todennäköisyys saada ainakin yksi ässä ja kakkonen on 0,2813 + 0,2813 - 0,498565 = 0,063962.
Mitkä ovat todennäköisyydet saada ruutujätkä 27 kädellä peräkkäin kuuden kortin pelissä?
Todennäköisyys saada se millä tahansa kädellä on 6/52. Todennäköisyys saada se 27 kädellä peräkkäin on (6/52) 27 = 1/20 989 713 842 161 800 000 000 000.
Mikä on todennäköisyys saada "kuolleen miehen käsi" eli kaksi paria ässää ja kasia?
On kuusi tapaa järjestää kaksi maata neljästä jokaiselle parille. Tällöin yksittäiselle korttiparille on 44 korttia. Joten onnistuneiden yhdistelmien lukumäärä on 6 * 6 * 44 = 1584. Yhteensä yhdistelmiä on 2 598 960, joten todennäköisyys on 0,0609 %.
Ymmärtääkseni olet jo vastannut kysymykseen "kuolleen miehen käden", kahden ässäparin ja kasin, saamisen todennäköisyys on 0,0609 % 3. huhtikuuta 2005 , mutta uskon, että kuolleen miehen käsi on "kaksi mustaa ässää, kaksi mustaa kasia ja ristien kuningatar". Mikä on todennäköisyys saada juuri tuo käsi yhdestä tavallisesta pakasta?
On vain yksi tapa saada täsmälleen tuo käsi. Joten todennäköisyys olisi 1 combin(52,5):ssä tai 1 2 598 960:ssä.
Mitkä ovat todennäköisyydet/kertoimet kullekin mahdolliselle viiden kortin kädelle, joka voitaisiin jakaa tavallisesta 52 kortin pakasta, jossa yhden, kertaamattoman kortin maata kädessä pidetään yleisenä? Tarkastellaan esimerkiksi kättä A♠ A♣ A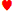 A
A 2. Tässä kädessä 2:n maata ei oteta huomioon, ja se edustaisi mitä tahansa pakan neljästä 2:sta. Toinen esimerkki on AJ-8-6-5. Tässä kädessä kaikkien viiden kortin maata ei oteta huomioon, joten vain yksi tällainen yhdistelmä voi esiintyä. Toinen esimerkki: 3♠ 3
2. Tässä kädessä 2:n maata ei oteta huomioon, ja se edustaisi mitä tahansa pakan neljästä 2:sta. Toinen esimerkki on AJ-8-6-5. Tässä kädessä kaikkien viiden kortin maata ei oteta huomioon, joten vain yksi tällainen yhdistelmä voi esiintyä. Toinen esimerkki: 3♠ 3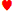 7♣ 7♠ Q. Tässä kädessä kahta kolmosta ja kahta nelosta ei jätetä huomiotta, vaikka niitä olisi useampi kuin yksi kädessä, mutta Q:n maa on geneerinen. Toisin sanoen minkä tahansa kortin maa, jota ei ole toistettu kädessä, jätetään huomiotta, ja kyseistä kättä pidetään yhtenä mahdollisista käsistä, vaikka käden uusiutumismahdollisuuksia olisi monia, jos kunkin kortin maata ei jätettäisi huomiotta. Näin ollen suora tai väri, joka koostuu viidestä tietystä kortista; sanotaan Q
7♣ 7♠ Q. Tässä kädessä kahta kolmosta ja kahta nelosta ei jätetä huomiotta, vaikka niitä olisi useampi kuin yksi kädessä, mutta Q:n maa on geneerinen. Toisin sanoen minkä tahansa kortin maa, jota ei ole toistettu kädessä, jätetään huomiotta, ja kyseistä kättä pidetään yhtenä mahdollisista käsistä, vaikka käden uusiutumismahdollisuuksia olisi monia, jos kunkin kortin maata ei jätettäisi huomiotta. Näin ollen suora tai väri, joka koostuu viidestä tietystä kortista; sanotaan Q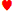 J♣ 10
J♣ 10 9
9 8♠ tai A♠ J♠ 8♠ 7♠ 3♠ voi esiintyä vain kerran, koska mikä tahansa muu samojen korttien yhdistelmä, vaikkakin eri maassa, olisi kaksoiskappale. Joten tätä kriteeriä käyttäen, mikä on minkä tahansa yksittäisen jaetun käden O/P? Toisin sanoen kuinka monta tällaista viiden kortin kättä on standardissa 52 kortin pakassa? Kiitos panoksestasi.
8♠ tai A♠ J♠ 8♠ 7♠ 3♠ voi esiintyä vain kerran, koska mikä tahansa muu samojen korttien yhdistelmä, vaikkakin eri maassa, olisi kaksoiskappale. Joten tätä kriteeriä käyttäen, mikä on minkä tahansa yksittäisen jaetun käden O/P? Toisin sanoen kuinka monta tällaista viiden kortin kättä on standardissa 52 kortin pakassa? Kiitos panoksestasi.
Tunnen tämän konseptin erittäin hyvin. Viiden kortin käsiä on 134 459 kappaletta. Tiedän, että tämä on ensimmäinen videopokeriohjelmani, joka analysoi kaikki 2 598 960 mahdollista kättä ja jonka voittotaulukon läpikäyminen vei päiviä. Kuitenkin ajamalla vain yhden kustakin 134 459 käsiluokasta, painottaen sitä kaikkien luokan käsien lukumäärällä, voi lyhentää suoritusaikaa 95 %. Joskus, kun peli on maakohtainen, kuten äskettäin tekemässäni Black Jack Bonus Poker -analyysissä, minun on pyyhittävä pölyt pois vanhasta ohjelmastani ja tehtävä se hitaasti.
Mitkä ovat todennäköisyydet Five Card Studissa, kun pakassa on viisi maata neljän sijaan?
Yhdistelmät viisisuopapokerissa
| Käsi | Yhdistelmät | Todennäköisyys | Kaava |
| Viisi samanlaista | 13 | 0,000002 | 13 |
| Värisuora | 50 | 0.000006 | 5*10 |
| Neloset | 3900 | 0,000472 | 13*12* YHTEISLÄHETYS (5,4)*5 |
| Huuhtele | 6385 | 0,000773 | 5*(YHDISTELMÄ(13,5)-10) |
| Täyskäsi | 15600 | 0,001889 | 13*12*KOMBIN(5;3)*KOMBIN(5;2) |
| Suoraan | 31200 | 0,003777 | 10*(5^5-5) |
| Kolmoset | 214500 | 0,025969 | 13*COMBIN(12,2)*COMBIN(5,3)*5^2 |
| Kaksi paria | 429000 | 0,051938 | YHDISTÄ(13,2)*11*YHDISTÄ(5,2)^2*5 |
| Pari | 3575000 | 0,432815 | 13*COMBIN(12,3)*COMBIN(5,3)*5^3 |
| Ei mitään | 3984240 | 0,48236 | (YHDISTELMÄ(13;5)-10)*(5^5-5) |
| Kokonais | 8259888 | 1 |
Huomaa, että käänsin täyskäden ja värin järjestyksen päinvastaiseksi.
Kuinka monessa viiden kortin korttiyhdistelmässä tavallisessa pelikorttipakassa on kortteja täsmälleen kahdesta maasta?
Kaksi maata voidaan jakaa joko 4 ja 1 tai 3 ja 2. Tarkastellaan ensin 4/1-jakoa. Neljän kortin maalle on valittavana neljä maata ja yhden kortin maalle kolme. 4 arvoa 13:sta voi valita combin(13,4) = 715 tavalla. Yksi arvo voi valita 13 tavalla. Joten 4/1-jakoon kahden maan välillä on 4 × 3 × 715 × 13 = 111 540 tapaa. Samalla logiikalla 3/2-jakoon on 4 × 3 × combin(13,3) × combin(13,2) = 267 696 tapaa. Kokonaistodennäköisyys on siis (111540 + 267696) / combin(52,5) = 14,59 %.
Mitkä ovat todennäköisyydet sille, että minulle jaetaan 2-3-4-5-7, jotka eivät ole samaa maata? Kiitos paljon, sivusto on mahtava!
Kiitos. (4 5 -4)/combin(52,5) = 1020/2598960 = 1/2 548.
Olin Foxwoodsissa toissapäivänä katsomassa Foxwoods Poker Classicin kahta viimeistä pöytää. Kun Vince Van Patten (yksi World Poker Tourin isännistä) tuli katsomaan, hän alkoi tehdä kaikenlaisia vetoja paikalla hengailevien pokeriammattilaisten kanssa. Hän tarjosi kenelle tahansa 20:1 kertoimen, jos he pystyisivät selaamaan koko korttipakan ja vaihtamaan rivejä keskenään sanoen ääneen jokaisen kortin kohdalla ässä, 2, 3, 4 ja niin edelleen aina kuninkaaseen asti ja aloittaen alusta ässällä ilman, että heidän ilmoittamaansa korttia koskaan tulisi esiin. Kukaan ei päässyt loppuun asti, ja Vince voitti muutaman sata dollaria noin 10 minuutissa ennen kuin kaikki luovuttivat. Tiedän, että tämän on oltava mahdollista, mutta epäilen, että Vincellä on melkoinen houkku tarjoten vain 20:1 kertoimen. Mitkä ovat todennäköisyydet saada koko pakka läpi?
Yksinkertainen tapa arvioida voittotodennäköisyyttä on olettaa, että jokaisella kortilla on 12/13 todennäköisyys olla vastaamatta ilmoitettua arvoa. Voittaakseen tämän vedon uhrin pitäisi onnistua 52 kertaa. 52 voiton todennäköisyys on (12/13) * 52 = 1,56 %. Kohtuullinen maksettava hinta olisi 63,2:1. Kertoimella 20:1 Vincellä olisi 67,3 %:n etu (aith!).
GM:n mukaan, joka on minua parempi matemaatikko, todellinen todennäköisyys on 1,6232727 %. Eron syynä on se, että jokaisen valinnan tulos korreloi positiivisesti edellisten valintojen kanssa.
Eilen pelatessamme yksi pelaajista, vanha viekas ja aggressiivinen pelaaja, haastoi pöydän vastustajia tekemään tasarahalla sivupanoksia flopissa. Tämä vanha äkäinen vei vetoa, että yksi flopin kolmesta kortista olisi joko ässä, kakkonen tai jätkä (joskus hän vaihtoi kolmea tunnistettavaa korttia). Mitkä ovat tämän vedon kertoimet? Viisauttasi arvostettaisiin suuresti.
Ennen kuin yhtään korttia nähdään, todennäköisyys sille, että flopilla ei tule kolmea arvoa, on combin (40,3)/combin(52,3) = 9880/22100 = 44,71%. Joten tällä kaverilla oli 10,59 %:n etu.
Oletetaan, että 52 kortin pakasta jaetaan viisi korttia ja ensimmäinen on kuningas. Mikä on todennäköisyys, että pakasta tulee ainakin yksi kuningas lisää? Näin tällaisen ässätehtävän, mutta en oikein pystynyt seuraamaan sitä. Kiitos avusta.
Mieluiten vastaan todennäköisyyskysymyksiin kombinatorisen funktion avulla. Tällä tavalla tehtynä pakassa on combin (48,4) = 194 580 tapaa valita neljä korttia, jotka eivät ole kuninkaita, 48 ei-kuninkaista. Pakassa olevien 51 kortin joukosta on combin(51,4) = 249 900 tapaa valita mitkä tahansa neljä korttia. Todennäköisyys sille, ettei seuraavissa neljässä kortissa saada yhtään kuningasta, on siis 194 580/249 900 = 77,86 %. Näin ollen todennäköisyys saada ainakin yksi laji on 100 % - 77,86 % = 22,14 %.
Useat ihmiset ovat sanoneet, että kombinatorinen funktio on luultavasti ylivoimainen tällaisille yksinkertaisille todennäköisyyskysymyksille. En ole tästä eri mieltä, mutta tämän sivuston tärkein syy on yrittää opettaa lukijoilleni jotain matematiikasta. Kombinatorinen funktio on erittäin hyödyllinen todennäköisyydessä ja säästää paljon aikaa. Käsillä olevaan kysymykseen voidaan kuitenkin helposti vastata ilman sitä.
Todennäköisyys sille, että toinen kortti ei ole kuningas, on 48/51. Tämä johtuu siitä, että pakassa on jäljellä 48 ei-kuningasta ja yhteensä 51 korttia jäljellä. Jos toinen kortti ei ole kuningas, todennäköisyys sille, että kolmaskaan kortti ei ole kuningas, on 47/50 (47 ei-kuningasta jaettuna 50 jäljellä olevalla kortilla). Tämän jälkeen todennäköisyys sille, että mikään neljästä muusta kortista ei ole kuningas, on (48/51) × (47/50) × (46/49) × (45/48) = 77,86 %. Todennäköisyys sille, että näin ei ole, eli että ainakin yksi kuningas on jäljellä, on 100 % - 77,86 % = 22,14 %.
Valitse ensin viisi korttia yhdestä 52 kortin pakasta. Toiseksi laske niiden blackjack-arvot (T, J, Q, K = 10, A = 1). Mikä on todennäköisyys, että summa on parillinen/pariton? Luulisin, että parillisten korttien ylitarjonnan vuoksi summa olisi paljon todennäköisemmin parillinen.
Yllättäen pariton kokonaissumma on todennäköisempi, 50,03 %, vaikka 52 kortista 30 on parillisia. Seuraava taulukko näyttää kunkin parillisen/parittoman jaon todennäköisyyden.
Pariton/parillinen kysymys
| Evens | Kertoimet | Yhdistelmät | Todennäköisyys | Summa |
| 0 | 5 | 15504 | 0,005965 | Pariton |
| 1 | 4 | 155040 | 0,059655 | Jopa |
| 2 | 3 | 565440 | 0,217564 | Pariton |
| 3 | 2 | 942400 | 0,362607 | Jopa |
| 4 | 1 | 719200 | 0,276726 | Pariton |
| 5 | 0 | 201376 | 0,077483 | Jopa |
| Kokonais | 2598960 | 1 |
Mikä on todennäköisyys, että jos nostat pakasta kolme korttia, tasan yksi niistä on pata?
Todennäköisyys sille, että ensimmäinen kortti on pata ja kaksi seuraavaa eivät, on (13/52) × (39/51) × (38/50) = 14,53 %. Tämä pitäisi sitten kertoa kolmella, koska pata voi olla mikä tahansa kolmesta kortista. Vastaus on siis 3 × 14,53 % = 43,59 %. Niille, jotka pitävät kombinatorisesta funktiosta, vastaus on 13 × combin(39,2) / combin (52,3) = 9 633 / 22 100 = 43,59 %.
Valitse kaksi satunnaislukua väliltä 0 ja 1 (tasaisesti jakautuneina). Valitse nyt näistä kahdesta pienempi. Mikä on valinnan keskiarvo? Entä yleisessä n luvun tapauksessa?
Kahdelle luvulle vastaus on 1/3 ja n luvulle 1/(n+1). Lähetin ratkaisut matemaattisten tehtävien sivulleni, kysymyksiin 194 ja 195.
Pelaat peliä, johon osallistuu kolme henkilöä: (a) sinä itse, (b) vastustajasi ja (c) tuomari. Jokainen teistä valitsee salaa reaaliluvun 0:n ja 1:n väliltä. Kun kaikki numerot on valittu, ne paljastetaan. Pelaaja, joka arvasi lähimmäksi tuomarin numeroa menemättä sen yli, voittaa. Jos olet lähempänä, voitat 1 dollarin. Jos vastustajasi on lähempänä, häviät 1 dollarin. Jos molemmat pelaajat menevät yli tai peli on tasapeli, peli on tasapeli.
Onko olemassa numero, jonka voit valita maksimoidaksesi odotetun tuoton, jos toinen pelaaja valitsee satunnaisesti? Entä jos toisella pelaajalla on myös strategia?
Toivottavasti olet tyytyväinen. Käytin koko päivän toiseen osaan, ja vastaukseni oli silti väärä. Jotta en riistäisi lukijoiltani samaa iloa, en vain tyrmää vastauksia tähän. Jaoin tämän kahteen tehtävään ja julkaisin vastaukset ja ratkaisut osoitteessa mathproblems.info , tehtävät 196 ja 197.
Jos valitset satunnaisesti viisi korttia tavallisesta 52 kortin pakasta, mikä on todennäköisyys, että kaikki neljä maata ovat mukana?
Yhdessä maassa pitäisi olla kaksi korttia ja kolmessa maassa yksi kortti per maa. Kahdesti esitetyssä maassa on neljä mahdollista maata. Kahdesti esitetyssä maassa on combin (13,2)=78 tapaa valita kaksi arvoa 13:sta. Jokaiselle muulle kolmelle maalle on 13 mahdollista arvoa. Joten yhdistelmien kokonaismäärä on 4 × 78 × 13 × 13 × 13 = 685 464. On combin(52,5)=2 598 960 tapaa valita viisi korttia 52:sta. Todennäköisyys on siis 685 464/2 598 960 = 26,37 %.
Mikä on todennäköisyys, että kaksi valittua arvoa, esimerkiksi kuningatar ja kuningas, esiintyvät peräkkäin satunnaisessa pakassa? Joku haastoi minut lyömään vetoa, että niin tapahtuisi.
Satunnaissimulaation mukaan todennäköisyys on 48,64 %. Joten olisin ottanut tuon vedon.
Voitko suositella funktiota, joka kuvaa mitkä tahansa viisi korttia 52 kortin pakasta kokonaisluvuksi 0 - 2 598 959?
Kyllä. Anna ensin jokaiselle kortille arvo väliltä 0–51. Kutsu kortteja arvoiksi c1–c5 ja järjestä ne siten, että c1 on pienin ja c5 suurin. Kutsu sitten seuraavaa funktiota:
int HaeIndeksi(int c1, int c2, int c3, int c4, int c5)
{
return combin(c5,5) + combin(c4,4)+ combin(c3,3) + combin(c2,2) + combin(c1,1);
}
Jos combin palauttaa perinteisen arvon, paitsi jos ensimmäinen arvo on pienempi kuin toinen arvo, palauta 0 seuraavasti:
int combin(int x, int y)
{
jos (y>x)
palauta 0;
muu
{
kokonaisluku i,n;
n=1;
for (i=x-y+1; i<=x; i++)
n*=i;
for (i=2; i<=y; i++)
n/=i;
return n;
}
}
Jos teet tämän käyttääksesi taulukon elementtiä, lataa taulukko seuraavasti.
määrä=0;
for (c5 = 4; c5 < 52; c5++)
{
for (c4 = 3; c4 < c5; c4++)
{
kun (c3 = 2; c3 < c4; c3++)
{
kun (c2 = 1; c2 < c3; c2++)
{
kun (c1 = 0; c1 < c2; c1++)
{
index_array[count]=MitäTottaVoitToivoa;
määrä++;
}
}
}
}
}
Mikä on todennäköisyys saada 10 värisuorasta 3, joista kolme on värisuorassa, jossa on yksi väli?

Tämä on binomijakauman tyyppinen ongelma. Yleinen kaava on, että jos tapahtuman todennäköisyys on p ja jokainen lopputulos on riippumaton, niin todennäköisyys sille, että tapahtuma tapahtuu täsmälleen w t yrityksestä, on yhdistettynä (t,w)×p w ×(1-p) tw .
Tässä tapauksessa on kaksi tapaa saada värisuora. Tarvitset ruudun 8 ja toisen kortin, jonka arvo on joko ruutu 6 tai J. Pakassa jäljellä olevista 47 kortista kaksi korttia voidaan nostaa combin(47,2) = 1 081 tavalla. Joten todennäköisyys saada värisuora millä tahansa kädellä on 2/1 081 = 0,0018501. Todennäköisyys saada 3 korttia 10:stä on combin(10,3) × 0,0018501 * 3 × (1 - 0,0018501) * 7 = 0,000000750178 eli 1/1 333 017.
Kaksi 54 kortin pakkaa (mukaan lukien kaksi jokeria) sekoitetaan yhteen. Pelaajalle annetaan puolet niistä. Mikä on todennäköisyys, että pelaaja sai kaikki neljä punaista kolmosta?
Punaisia kolmosia on neljä ja muita kortteja 104. On vain yksi tapa saada kaikki neljä punaista kolmosta. Pelaaja voi saada 50 muuta 104 korttia seuraavasti: combin (104,50)=1,46691 × 10^ 28 . Yhdistelmien kokonaismäärä on combin(108,54)=2,48578 × 10^ 30 . combin(104,50)/combin(108,54) = 0,059012.
Jos et pidä niin suurten lukujen käsittelystä, tässä on vaihtoehtoinen ratkaisu. Numeroi neljä punaista kolmosta 1–4. Todennäköisyys sille, että ensimmäinen punainen kolmoset ovat pelaajan pinossa, on 54/108. Poista nyt ensimmäiset kolme. Todennäköisyys sille, että pelaajalla on toinen punainen kolmoset, on 53/107, koska pelaajalla on jäljellä 53 korttia ja jäljellä on 107 korttia. Samoin todennäköisyys sille, että pelaajalla on kolmas punainen kolmoset, on 52/106 ja neljäs punainen kolmoset on 51/105. (54/108) × (53/107) × (52/106) × (51/105) = 0,059012.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Mielenkiintoista. Kuten kirjoitin, arvioin tuon käden tapahtuvan noin kerran 23,7 vuodessa missä tahansa Nevadassa. Sanoisin, että se oli yksi niistä ajoista.
Oletetaan, että valitset kaksi arvomerkkiä, esimerkiksi kuninkaat ja kuningattaret. Mikä on todennäköisyys, että satunnaisesti sekoitetussa 52 kortin pakassa ainakin kerran kuningas ja kuningatar ovat vierekkäin?
Saan 48,6279 %. Jos haluat lyödä vetoa siitä, reilu kertoimella "kyllä"-vastaukselle olisi 1,0564:1.
Kuulin äskettäin, että bridgessä oli "täydellinen" peli, jossa jokainen pelaaja sai 13 korttia yhtä neljästä maasta. Mitkä ovat sen todennäköisyydet?
Huhujen mukaan sama tapahtui myös whist-pelissä Warwickshiressä vuonna 2011. Muiden lukijoiden tiedoksi, mikä on todennäköisyys jakaa 52 kortin pakka neljään 13 kortin ryhmään, joissa jokainen paketti koostuu kokonaan yhden maan 13 kortista.
Yhdistelmä(52,13)*yhdistelmä(39,13)*yhdistelmä(26,13) = 53 644 737 765 488 800 000 000 000 000 mahdollista tapaa järjestää 52 korttia neljään 13 kortin settiin. 4! = 24 olisi voittoyhdistelmien lukumäärä, koska voit jakaa neljä maata neljälle pelaajalle haluamallasi tavalla. Joten todennäköisyys on 1/2 235 197 406 895 370 000 000 000 000. Antaaksemme tälle luvulle hieman perspektiiviä, jos kaikki maapallon 7,5 miljardia ihmistä jakaisivat bridge-käden yhden käden sekunnissa, todennäköisyys sille, että joku jakaisi niin sanotun täydellisen käden ennen auringon räjähdystä 5 miljardin vuoden kuluttua, on 1/16 558.
Jotkut kuitenkin määrittelevät "täydellisen" käden siten, että vain yksi pelaaja saa kaikki 13 korttia mitä tahansa maata. Osoitan, että tämän todennäköisyys on 1 39 688 347 497 pelistä. Näin luultavasti tapahtuu silloin tällöin jossain päin maailmaa.
Mikä on todennäköisyys Texas Hold'emissa sille, että kahdella pelaajalla on väri samassa kädessä, ja molemmat käyttävät molempia taskukorttejaan?
Määritetään ensin pelaajan ja pelilaudan korttien yhdistelmien lukumäärä, jossa tämä voi tapahtua. Maata on luonnollisesti neljä. Sitten on combin(13,4)=715 tapaa valita neljä annetusta maasta 13 kortista.
Toiseksi, yksi tapa, jolla tämä voi tapahtua, on se, että pelaajilla on laudalla kolme samaa maata olevaa korttia ja kaksi muuta 39 muun kortin joukossa. Laudalla voi olla kolme yhdeksästä jäljellä olevasta kortista valitusta maasta 84 tavalla. Sitten on combin(9,3) = 741 tapaa valita kaksi lisää korttia 39:stä muusta kolmesta maasta. Joten laudalla on 84 * 741 = 62 244 tapaa, joilla kolme kyseistä maata on laudalla.
Kolmanneksi, toinen tapa on, että pelaajilla on laudalla neljä samaa maata olevaa korttia ja yksi muiden 39 kortin joukossa. Laudalla voi olla neljä yhdeksästä jäljellä olevasta kortista valitusta maasta combin(9,4) = 126 tavalla. Sitten on 39 tapaa valita yksi kortti lisää 39 muun maan joukosta. Kaikki nämä eivät kuitenkaan johda siihen, että molemmat pelaajat käyttävät molempia taskukortteja. Jotta tämä ehto täyttyisi, laudalla on oltava kyseisen maan pienimmän kortin. Todennäköisyys sille, että kahdeksasta pelissä olevasta kortista on 4/8 = 1/2, on siis 126 * 39 * (1/2) = 2 457 tapaa, joilla laudalla on neljä kyseistä maata.
Neljänneksi, viimeinen tapa, jolla tämä voi tapahtua, on se, että pelaajilla on pöydällä viisi samaa maata olevaa korttia. Pöydällä voi olla viisi yhdeksästä jäljellä olevasta kortista valitusta maasta combin(9,5)=126 tavalla. Kaikki nämä eivät kuitenkaan johda siihen, että molemmat pelaajat käyttävät molempia taskukortteja. Jotta tämä ehto täyttyisi, pöydällä on oltava kaksi pienintä korttia kyseisestä maasta. Todennäköisyys sille, että yhdeksästä pelissä olevasta kortista on samaa maata, on combin(5,2)/combin(9,2) = 10/36 = 5/18. Joten pöydällä on 126 * (5/18) = 35 tapaa, joilla neljä kyseistä maata on jäljellä.
Joten yhdistelmien lukumäärä, joissa tämä tapahtuu, on 715 * (62 244 + 2 457 + 35) = 46 286 240.
Kokonaiskombinaatioiden kokonaismäärä, joilla pelaajan taskukorteiksi voidaan valita neljä korttia 52:sta ja sitten viisi lisää 48:sta jäljellä olevasta pöydästä, on combin(52,4)*combin(48,5) = 463 563 500 400.
Todennäköisyys on siis 46 286 240 / 463 563 500 400 = 0,000399395 = 1/2 504.
Tätä kysymystä esitettiin ja siitä keskusteltiin foorumillani Wizard of Vegasissa .
Kasinon jakaja työstää uutta Three Card Poker -varianttia. Hän ottaa kaikki kuvakortit tavallisesta pakasta ja sekoittaa ne huolellisesti. Sitten hän jakaa kolme korttia pelaajalle 1, kolme korttia pelaajalle 2, kolme korttia pelaajalle 3 ja loput kolme korttia pelaajalle 4. Mikä on todennäköisyys, että kaikissa neljässä kädessä on suora (JQK mistä tahansa maasta)?
Jaa yhdelle pelaajalle kerrallaan. Todennäköisyys sille, että ensimmäinen pelaaja saa yhden jokaisesta arvosta, on 4^3/combin(12,3) = 64/220.
Olettaen, että ensimmäinen pelaaja sai suoran, pakassa on jäljellä kolme korttia jokaista arvoa. Todennäköisyys sille, että toinen pelaaja saa yhden kortin jokaista arvoa, on 3^3/combin(9,3) = 27/84.
Olettaen, että kaksi ensimmäistä pelaajaa saivat suoran, pakassa on jäljellä kaksi korttia kummastakin arvosta. Todennäköisyys sille, että kolmas pelaaja saa yhden kortin kummastakin arvosta, on 2^3/combin(6,3) = 8/20.
Olettaen, että kolme ensimmäistä pelaajaa saivat suoran, pakassa on jäljellä yksi jokaisesta arvosta kortteja. Nämä kolme korttia muodostavat luonnollisesti suoran.
Näin ollen todennäköisyys sille, että kaikki neljä pelaajaa saavat suoran, on (64/220)*(27/84)*(8/20)*1 = 216/5775 = 72/1925 = 3,74%.
Tätä kysymystä on kysytty ja siitä keskusteltu foorumillani Wizard of Vegasissa, alkaen tästä viestistä .
Oletetaan, että minulla on 48 kortin pakka, neljä maata, kaksitoista korttia jokaisesta maasta. Jos nostan 15 korttia, mikä on todennäköisyys, että nostan ainakin yhden kortin jokaisesta maasta?
Aloitetaan 100 prosentista ja vähennetään siitä todennäköisyydet, joiden tuloksena on alle neljä maata.
Mikä on esimerkiksi todennäköisyys sille, että 48 kortilla ei ole sydäntä? Kortteja, jotka eivät ole sydämiä, on 36. Tapojen määrä valita 15 korttia 36:sta on combin(36,15) = 5 567 902 560. Tapojen määrä valita 15 korttia kaikista 48:sta on 1 093 260 079 344. Joten todennäköisyys sille, että 15 kortilla ei ole sydäntä, on 5 567 902 560 / 1 093 260 079 344 = 0,005093.
Kerrotaanpa seuraavaksi tämä neljällä, jotta saadaan todennäköisyys sille, että mikä tahansa maa, ei vain hertta, häviää: 4 × combin(36,15)/combin(48,15) = 0,02037174.
Tämä kuitenkin laskee joissakin tilanteissa kaksinkertaisesti. Ajatellaanpa, että saat 15 mustaa korttia. Se jättäisi pois sekä hertta- että ruutukortit. Olisimme laskeneet tuon tilanteen kaksinkertaisesti. Joten meidän on korjattava tämä. On combin(4,2) = 6 tapaa valita kaksi maata neljästä. Todennäköisyys sille, että kaikki 15 korttia ovat mitä tahansa kahta tiettyä maata, on combin(24,15)/combin(48,15) = 1307504/1 093 260 079 344 = 0,00000120. Kuten mainittiin, on kuusi tapaa valita kaksi maata neljästä, joten kaikkien korttien kahden maan lukumäärä on 6 × combin(24,15)/combin(48,15) = 0,00000718.
Vähentämällä kaksinkertaisesti lasketun määrän saamme kahden tai kolmen maan esiintymisen todennäköisyydeksi 0,02037174 - 0,00000718 = 0,02036456.
Huomaa, että meidän ei tarvitse huolehtia yhden maan edustuksesta, koska on mahdotonta valita 15 korttia 12:sta.
Viimeisenä vaiheena vähennä 100 prosentista 2 tai 3 maan todennäköisyys saadaksesi kaikkien neljän maan todennäköisyyden: 1,00000000 - 0,02037174 = 0,97963544.
Tätä kysymystä on kysytty ja siitä keskusteltu foorumillani Wizard of Vegasissa .
Jos jakaisin 13 korttia sekoitetusta (oletettavasti satunnaisesta) korttipakasta, kuinka monta erilaista arvojärjestystä minun pitäisi odottaa näkeväni?
Tämä on Markov-ketjun tyyppinen ongelma, jos sellainen koskaan on ollut.
Seuraava taulukko näyttää odotetun arvojärjestyksen 0–4 kortilla kaikille jaettujen korttien määrille 1–52.
Odotetut arvot jaettujen korttien mukaan
| Kortit | 0 Sijoitukset | 1. sijoitus | 2 tasoa | 3 tasoa | 4 tasoa | Odotettu Arvot |
|---|---|---|---|---|---|---|
| 1 | 12.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
| 2 | 11.058824 | 1.882353 | 0,058824 | 0.000000 | 0.000000 | 1.941176 |
| 3 | 10.174118 | 2.654118 | 0,169412 | 0,002353 | 0.000000 | 2.825882 |
| 4 | 9.343577 | 3.322161 | 0,324994 | 0,009220 | 0.000048 | 3.656423 |
| 5 | 8.564946 | 3.893157 | 0,519088 | 0,022569 | 0.000240 | 4.435054 |
| 6 | 7.836014 | 4.373589 | 0,745498 | 0,044178 | 0,000720 | 5.163986 |
| 7 | 7.154622 | 4.769748 | 0.998319 | 0,075630 | 0,001681 | 5.845378 |
| 8 | 6.518655 | 5.087731 | 1.271933 | 0.118319 | 0,003361 | 6.481345 |
| 9 | 5.926050 | 5.333445 | 1.561008 | 0,173445 | 0,006050 | 7.073950 |
| 10 | 5.374790 | 5.512605 | 1.860504 | 0.242017 | 0.010084 | 7.625210 |
| 11 | 4.862905 | 5.630732 | 2.165666 | 0,324850 | 0,015846 | 8.137095 |
| 12 | 4.388475 | 5.693157 | 2.472029 | 0,422569 | 0,023770 | 8.611525 |
| 13 | 3.949628 | 5.705018 | 2.775414 | 0,535606 | 0,034334 | 9.050372 |
| 14 | 3.544538 | 5.671261 | 3.071933 | 0,664202 | 0,048067 | 9.455462 |
| 15 | 3.171429 | 5.596639 | 3.357983 | 0.808403 | 0,065546 | 9.828571 |
| 16 | 2.828571 | 5.485714 | 3.630252 | 0,968067 | 0,087395 | 10.171429 |
| 17 | 2.514286 | 5.342857 | 3.885714 | 1.142857 | 0.114286 | 10.485714 |
| 18 | 2.226939 | 5.172245 | 4.121633 | 1.332245 | 0,146939 | 10.773061 |
| 19 | 1.964946 | 4.977863 | 4.335558 | 1.535510 | 0,186122 | 11.035054 |
| 20 | 1.726771 | 4.763505 | 4.525330 | 1.751741 | 0,232653 | 11.273229 |
| 21 | 1.510924 | 4.532773 | 4.689076 | 1.979832 | 0,287395 | 11.489076 |
| 22 | 1.315966 | 4.289076 | 4.825210 | 2.218487 | 0,351261 | 11.684034 |
| 23 | 1.140504 | 4.035630 | 4.932437 | 2.466218 | 0.425210 | 11.859496 |
| 24 | 0,983193 | 3.775462 | 5.009748 | 2.721345 | 0,510252 | 12.016807 |
| 25 | 0,842737 | 3.511405 | 5.056423 | 2.981993 | 0.607443 | 12.157263 |
| 26 | 0,717887 | 3.246098 | 5.072029 | 3.246098 | 0,717887 | 12.282113 |
| 27 | 0.607443 | 2.981993 | 5.056423 | 3.511405 | 0,842737 | 12.392557 |
| 28 | 0,510252 | 2.721345 | 5.009748 | 3.775462 | 0,983193 | 12.489748 |
| 29 | 0.425210 | 2.466218 | 4.932437 | 4.035630 | 1.140504 | 12.574790 |
| 30 | 0,351261 | 2.218487 | 4.825210 | 4.289076 | 1.315966 | 12.648739 |
| 31 | 0,287395 | 1.979832 | 4.689076 | 4.532773 | 1.510924 | 12.712605 |
| 32 | 0,232653 | 1.751741 | 4.525330 | 4.763505 | 1.726771 | 12.767347 |
| 33 | 0,186122 | 1.535510 | 4.335558 | 4.977863 | 1.964946 | 12.813878 |
| 34 | 0,146939 | 1.332245 | 4.121633 | 5.172245 | 2.226939 | 12.853061 |
| 35 | 0.114286 | 1.142857 | 3.885714 | 5.342857 | 2.514286 | 12.885714 |
| 36 | 0,087395 | 0,968067 | 3.630252 | 5.485714 | 2.828571 | 12.912605 |
| 37 | 0,065546 | 0.808403 | 3.357983 | 5.596639 | 3.171429 | 12.934454 |
| 38 | 0,048067 | 0,664202 | 3.071933 | 5.671261 | 3.544538 | 12.951933 |
| 39 | 0,034334 | 0,535606 | 2.775414 | 5.705018 | 3.949628 | 12.965666 |
| 40 | 0,023770 | 0,422569 | 2.472029 | 5.693157 | 4.388475 | 12.976230 |
| 41 | 0,015846 | 0,324850 | 2.165666 | 5.630732 | 4.862905 | 12.984154 |
| 42 | 0.010084 | 0.242017 | 1.860504 | 5.512605 | 5.374790 | 12.989916 |
| 43 | 0,006050 | 0,173445 | 1.561008 | 5.333445 | 5.926050 | 12.993950 |
| 44 | 0,003361 | 0.118319 | 1.271933 | 5.087731 | 6.518655 | 12.996639 |
| 45 | 0,001681 | 0,075630 | 0.998319 | 4.769748 | 7.154622 | 12.998319 |
| 46 | 0,000720 | 0,044178 | 0,745498 | 4.373589 | 7.836014 | 12.999280 |
| 47 | 0.000240 | 0,022569 | 0,519088 | 3.893157 | 8.564946 | 12.999760 |
| 48 | 0.000048 | 0,009220 | 0,324994 | 3.322161 | 9.343577 | 12.999952 |
| 49 | 0.000000 | 0,002353 | 0,169412 | 2.654118 | 10.174118 | 13.000000 |
| 50 | 0.000000 | 0.000000 | 0,058824 | 1.882353 | 11.058824 | 13.000000 |
| 51 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 12.000000 | 13.000000 |
| 52 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 13.000000 | 13.000000 |
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Joku haastoi minut seuraavaan vetoon. Saan valita mitkä tahansa kolme arvoa tavallisesta pokeripakasta ja kirjoittaa ennusteeni muistiin, mutta pitää sen piilossa loppuun asti. Esimerkiksi 7-ässä-2. Sitten hän tarjoutui lyömään vetoa tasarahasta, että osaisi nimetä ainakin yhden arvoistani, jos saisi kolme arvausta. Mitkä olivat voittomahdollisuuteni?
Voittaaksesi vastustajasi on oltava väärässä kaikissa kolmessa ennustuksessa. Ensimmäisellä ennustuksella on 10/13 todennäköisyys olla väärä. Toisella ennustuksella on 9/12 todennäköisyys olla väärä, koska voimme poistaa ensimmäisenä arvatun sijan mahdollisuuksien joukossa. Kolmannella ennustuksella on 8/11 todennäköisyys olla väärä, koska voimme poistaa kaksi ensimmäistä arvattua sijaa mahdollisuuksien joukossa.
Kaikkien näiden kolmen asian pitäisi tapahtua, jotta voitat. Näin ollen voittomahdollisuutesi ovat (10/13) * (9/12) * (8/11) = 720/1716 = 41,96 %.
Tasapelitilanteessa talon etu tässä vedossa on sinun puoleltasi 16,08 % (auts!).
Tämä kysymys on poimittu Owen E'Shean teoksesta The Book of Proposition Bets (numero 7).
Joku haastoi minut lyömään vetoa, että hän pystyisi heittämään kahdella nopalla yhteensä 12 27 heiton aikana. Jos hän ei onnistuisi, voittaisin tasarahat. Koska 12:n heiton todennäköisyys on 1/36, eikö hänen pitäisi heittää keskimäärin 36 kertaa saadakseen 12? Näyttäisi siltä, että kertoimet olisivat minun puolellani, jos vastustajani saisi vain 27 heittoa. Olenko oikeassa, vai missä on laskuvirhe?
Keskimääräinen odotusaika 12:n välillä on todellakin 36 heittoa, mukaan lukien itse 12:n heitto. Se ei kuitenkaan tarkoita, että ne tulevat täsmälleen joka 36. heiton välein. Todennäköisyys sille, ettei heitetä 12:ta, on (35/36). Todennäköisyys sille, ettei sitä tehdä 27 heiton aikana, on (35/36)^27. Joten todennäköisyys sille, että ainakin 12:lla heitetään, on 1-(35/36)^27 = 53,26 %.
Seuraava taulukko näyttää todennäköisyyden saada vähintään luku 12 20–36 heitolla. Huomaa, että tasatilanteessa edun saavuttamiseksi tarvitaan 25 lukua.
Todennäköisyys 12
| Rullat | Todennäköisyys |
|---|---|
| 20 | 43,07 % |
| 21 | 44,66 % |
| 22 | 46,19 % |
| 23 | 47,69 % |
| 24 | 49,14 % |
| 25 | 50,55 % |
| 26 | 51,93 % |
| 27 | 53,26 % |
| 28 | 54,56 % |
| 29 | 55,82 % |
| 30 | 57,05 % |
| 31 | 58,24 % |
| 32 | 59,40 % |
| 33 | 60,53 % |
| 34 | 61,63 % |
| 35 | 62,69 % |
| 36 | 63,73 % |
Tiedämme, että mahdollisia viiden kortin yhdistelmiä 52:sta on combin(52,5)=2 598 960. Kysymykseni kuuluu, kuinka monta mahdollista viiden kortin kättä on mahdollista saada viiden pakan kengästä?
Otetaan tämä yksi käsityyppi kerrallaan.
- Viisi samanlaista korttia: Pakassa on 52 erilaista korttia, jotka muodostavat 52 yhdistelmää.
- Nelonen samasta kortista: Neloselle on 52 mahdollista korttia ja singletonille 51. Neloselle on siis 52 * 51 = 2 652 mahdollista yhdistelmää.
- Kolme samaa korttia ja kaksi toista korttia: Kolmelle samanlaiselle kortille on 52 mahdollista korttia ja parille 51. Täyskädelle on siis 52 * 51 = 2 652 mahdollista yhdistelmää.
- Kolme samanlaista korttia ja kaksi erilaista yksittäiskorttia: Kolmelle samanlaiselle kortit ovat mahdollisia 52 ja kahdelle yksittäiskortille combin(51,2)=1 275. Kolmosille on siis 52 * 1 275 = 66 300 mahdollista yhdistelmää.
- Kaksi paria samoja kortteja ja yksi singleton: Kahden eri kortin parit muodostavat combin(52,2) = 1 326 yhdistelmää. Sitten singletonille jää 50 yhdistelmää. Joten kahdelle parille on 1 326 * 50 = 66 300 mahdollista yhdistelmää.
- Yksi saman kortin pari ja kolme yksittäiskorttia: Parille on 52 mahdollista korttia. Sitten on combin(51,3) = 20 825 tapaa valita 3 korttia jäljellä olevista 51 kortista yksittäiskorteille. Joten parin yhdistelmien lukumäärä on 52 * 20 825 = 1 082 900.
- Viisi yksittäistä korttia: Viisi korttia 52:sta voi valita combin(52,5)=2 598 960 tavalla.
Kaikkien näiden yhdistelmien summa on 3 819 816.
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .


