Texas Hold ’Em - Todennäköisyys - Yleistä
Mitkä ovat todennäköisyydet sille, että samalle pelaajalle jaetaan kaksi nelosta ja värisuora Texas hold 'em -pelissä, jossa on kymmenen pelaajaa 50 kädessä?
Nelosen todennäköisyys seitsemässä kortissa on 0,00168067 ja värisuoran todennäköisyys 0,00027851. Jos x on nelosen todennäköisyys ja y on värisuoran todennäköisyys, niin pyytämäsi todennäköisyys on combin(50,2)*48* x² *y*(1-xy) ^47 . Vastaus on 0,0000421845 eli 1/23 705.
Mitkä ovat tilastolliset todennäköisyydet saada värin Texas Hold'emissa? Onko värin saaminen pelaajana helpompaa 7 Card Studissa vai Hold'emissa?
Voit katsoa pokerin todennäköisyyksiä käsittelevästä osiostani, että todennäköisyys on 3,03 %. Kertoimet ovat samat sekä Texas hold 'emissa että 7-card studissa.
Mitkä ovat todennäköisyydet saada kuningasvärisuora Texas hold'emissa riverillä?
Niille lukijoille, jotka eivät tiedä, river on viides ja viimeinen yhteinen kortti Texas hold'emissa. Pelaajan on muodostettava paras pokerikäsi omien kahden korttinsa ja viiden yhteisen kortin välillä. Eli kysyt, mikä on todennäköisyys sille, että pelaaja muodostaa kuningasvärisuoran seitsemällä kortilla ja että seitsemäs jaettu kortti on osa kuningasvärisuoraa. Todennäköisyys muodostaa viiden kortin kuningasvärisuora seitsemällä kortilla ennen korttien huomioon ottamista on 4 * combin(47,2) / combin(52,7) = 4324/133784560 eli 1/30940. Todennäköisyys sille, että seitsemäs kortti on osa kuningasvärisuoraa, on 5/7. Joten lopullinen todennäköisyys on 21620/936491920 eli 1/43316.
Mitkä ovat todennäköisyydet saada Texas Hold'missa yhden tai kahden aukon sisäsuoraan viidennellä kadulla flopista alkaen?
Lukijoideni avuksi tässä kysymyksessä kysytään, mikä on todennäköisyys täyttää yksi tai kaksi aukkoa suoraan kahdella lisäkortilla, kun pakassa on jäljellä 47. Yhden aukon tapauksessa todennäköisyys on 1 - combin(43,2) / combin(47,2) = 0,164662. Kahden aukon tapauksessa todennäköisyys on 4 2 / combin(47,2) = 0,0148.
Texas Hold'emissa, jos flopin kortit ovat kaikki samaa maata, mikä on todennäköisyys, että jollakin pelaajalla on kaksi muuta samaa maata olevaa korttia?
Samaa maata on jäljellä 10 korttia ja pakassa on jäljellä 49. Todennäköisyys on siis combin(9,2)/combin(49,2) = 36/1176 = 0,0306.
Ovatko eri käsien todennäköisyydet samat Texas Hold'emissa ja Seven-Card Studissa vai eroavatko ne jotenkin yhteiskorttien vuoksi? Voisitko selittää miksi tai miksi ei?
Kyllä, todennäköisyydet ovat samat. Seitsemällä satunnaisella kortilla 52:sta on samat kertoimet riippumatta siitä, miten ne otetaan pakasta tai kenen kanssa ne jaetaan.
Voitko kertoa minulle kahden ensimmäisen kortin perusteella, mitkä ovat todennäköisyydet saada 35 kädessä 7 kättä, joissa on Ace King tai parempi hold'emissa?
Ässän/kuninkaan saamisen todennäköisyys on (8/52)*(4/51) = 0,012066. Minkä tahansa parin saamisen todennäköisyys on (3/51) = 0,058824. Joten parin tai paremman saamisen todennäköisyys on 0,07089. Todennäköisyys saada tasan seitsemän kättä, joissa on ässä/kuningas tai parempi, on combin(35,7)*(.07089)^7*(1-.07089)^28 = 0,00772. Laskeaksemme 7:n tai suuremman todennäköisyyden meidän pitäisi käydä läpi yhteensä 7–35 kättä yksi kerrallaan. Tämä on yhteensä 0,010366551.
Miten arvioisit todennäköisyyden saada neljän kortin väri tai parempi flopilla holdemissa, jos taskukorttisi ovat samaa maata?
Todennäköisyys saada kaksi lisää samaa maata on 39*combin(11,2)/combin(50,3) = 0,109439. Todennäköisyys saada kolme lisää samaa maata on combin(11,3)/combin(50,3) = 0,008418. Joten todennäköisyys saada ainakin kaksi lisää samaa maata on 0,117857.
Herra Velho, Ensinnäkin haluan sanoa, että sinulla on mahtava sivusto! Olen lukenut sitä jo jonkin aikaa. Tarkistin pokerikysymykset, mutta en nähnyt tätä. Toinen sivusto väittää seuraavaa: "Texas Hold'emissa todennäköisyys sille, että AK jaetaan ennen floppia ja riverillä saa A:n tai K:n, on 1/2 (parillinen)." Tämä vaikuttaa intuitiivisesti aivan liian korkealta. Mitä mieltä olet? Kiitos vielä kerran!
Kiitos myös sinulle ystävällisistä sanoistasi. Niille, jotka eivät tunne hold'emia, tämä kysymys on kuin kysyisi, että jos pelaajalle jaettaisiin ässä ja kuningas sekä viisi satunnaista korttia jäljellä olevista 50 kortista, mikä on todennäköisyys, että pelaaja muodostaisi kuninkaan ja/tai ässän pariksi? Muista 50 kortista 44 ei ole kuninkaita tai ässää. Tapojen lukumäärä mitkä tahansa viisi korttia 44:stä on combin(44,5) = 1 086 088. Tapojen lukumäärä mitkä tahansa viisi korttia kaikista 50:stä on combin(50,5) = 2 118 760. Joten todennäköisyys sille, ettei ässää ja/tai kuningasta muodosteta pariksi, on 1086088/2118760 = 51,26 %. Näin ollen todennäköisyys, että muodostatte parin, on 1-51,26 % = 48,74 %. Tämä on melko lähellä 1:2.
Mikä on todennäköisyys, että kahdella pelaajalla on erilaiset neloset Texas Hold'emissa?
Kahdella pelaajalla on yhteensä 9 korttia. Näiden on koostuttava kahdesta nelosesta ja yhdestä yksittäisestä kortista. Yhdistelmien lukumäärä on combin(13,2)*44 = 3432. Yhteensä tapoja valita 9 korttia 52:sta on combin(52,9) = 3 679 075 400. Todennäköisyys sille, että sinulla on oikeat kortit, mutta ei välttämättä oikeassa järjestyksessä, on 3432/3 679 075 400 = 1/1 071 992.
Vaikka kortit olisivat muotoa AAAABBBBC, se ei tarkoita, että molemmilla pelaajilla olisi erilaiset neloset. Ne voidaan järjestää viiden kortin kädeksi ja kahdeksi kahden kortin kädeksi 9!/(5!*2!*2!) = 756 eri tavalla. Seuraavassa on lueteltu tavat, joilla nämä 9 korttia voivat pudota jakoon.
Neloset huonojen lyöntien yhdistelmät
Pelaaja 1 | Pelaaja 2 | Floppi | Peilikuviot | Yhdistelmät kuviota kohden | Yhdistelmiä yhteensä |
AA | BB | AABBC | 2 | 72 | |
AA | AB | ABBBC | 4 | 48 | 192 |
AA | AA | BBBBC | 2 | 6 | 12 |
AA | Ilmastointilaite | ABBBB | 4 | 12 | 48 |
AA | eaa. | AABBB | 4 | 24 | 96 |
AB | AB | AABBC | 1 | 144 | 144 |
AB | Ilmastointilaite | AABBB | 4 | 48 | 192 |
Näistä vain ensimmäisessä ja viidennessä ryhmässä molemmilla pelaajilla on erilaiset neloset. Todennäköisyys sille, että AAAABBBBC-korttisetti johtaa kahteen erilaiseen neloseen, on 168/756 = 22,22 %.
Joten vastaus kysymykseesi on (3432/3 679 075 400)*(168/756) = 1/4 823 963. Käytännöllisemmin ottaen Party Pokerissa on bad beat -jättipotti, jos häviävä käsi on neljä kasia. Koska nelosia on kaksi, todennäköisyys sille, että molemmat ovat kaseja tai suurempia, on combin(7,2)/combin(13,2) = 21/78 = 26,92%. Joten todennäköisyys sille, että kahden pelaajan yhteinen käsi johtaa tähän bad beat -jättipottiin, on 1/17 917 577.
Eilen illalla pelaaja tarjosi minulle sivupanosta Texas Hold'emissa. Hän sanoi, että flopilla ilmestyisi ainakin yksi kuvakortti (tai mitkä tahansa kolme arvokorttia) ja tarjosi tasarahaa? Olisiko minun pitänyt hyväksyä panos?
Tapojen lukumäärä, joilla voit valita 3 korttia 40:stä ei-kuvakortista, on (40*39*38)/(1*2*3) = 9880. Tapojen lukumäärä, joilla voit valita 3 korttia 52:sta, on (52*51*50)/(1*2*3) = 22100. Todennäköisyys sille, ettei saat kuvakorttia, on siis 9880/22100 = 44,71 %. Näin ollen kuvakortin saamisen todennäköisyys on 55,29 %. Hänen puolellaan vedossa oli 10,58 %:n etu.
Kun pelaan Texas Hold'emia 10 pelaajan kanssa käyttäen tavallista 52 kortin pakaa ja kun jokaiselle pelaajalle on jaettu kaksi ensimmäistä korttia, mikä on todennäköisyys sille, että "flop" (seuraavat kolme korttia) ovat kaikki samaa maata? Onko sillä merkitystä, jos kädessäni on molemmat kortit samaa maata ja/tai eri maata?
Ennen omien korttiesi tarkastelua todennäköisyys on 4 × combin (13,3) / combin(52,3) = 5,1764706 %.
Toinen tapa tarkastella asiaa on (12/51) todennäköisyys sille, että flopin toinen kortti on samaa maata kuin ensimmäinen kortti. Todennäköisyys sille, että flopin kolmas kortti on sama maata, on (11/50). (12/51) × (11/50) = 5,1764706 %.
Todennäköisyys muuttuu hieman, jos tarkastelet omia korttejasi. Jos sinulla on kaksi samaa maata olevaa korttia, niin flopin todennäköisyys samaan maahan on pr(värisuora samassa maassa) + pr(värisuora eri maassa) = combin(11,3)/combin(50,3) + 3 × combin(13,3)/combin(50,3) = 5,2193878%.
Jos sinulla on kaksi eri maata olevaa korttia, niin flopin todennäköisyys saada sama maa on pr(värisuora yhteisessä maassa) + pr(värisuora eri maassa) = 2 × combin(12,3) / combin(50,3) + 2 × combin(13,3) / combin(50,3) = 5,1632653%.
Rakas velho, kunpa minulla olisi sinun aivosi. Joka tapauksessa kamppailuni tilastojen kanssa jatkuu. Yritän keksiä kaavaa, jolla voisin laskea värin saamisen todennäköisyyden flopilla, turnilla ja riverillä (texas hold'em) sen perusteella, ovatko taskukorttini samaa maata vai eivät. Kokeilin C(50,2) / C(47,5) -kaavoja, mutta se ei toiminut samaa maata saaneella parilla riverillä... Minun olisi pitänyt kiinnittää enemmän huomiota koulussa! Kiitos! Suurin fanisi.
Kiitos ystävällisistä sanoista, mutta en ole niin fiksu. Pari vuotta sitten osallistuin Mensan pääsykokeeseen, enkä päässyt vaadittuun kahteen prosenttiin. Olen edelleen järkyttynyt siitä, etteivät he suostuneet kertomaan minulle, kuinka hyvin pärjäsin. Tammikuun 13. päivänä Vegasissa järjestetään Jeopardy-kokeilut, joihin minulla on aika, ja olen varma, että mokaan sielläkin. Joka tapauksessa, vastauksena kysymykseesi tässä:
Suittien taskukorttien kanssa:
Väri flopin jälkeen: combin (11,3)/combin(50,3) = 165/19600 = 0,842%.
Väri vuoron jälkeen: (combin(11,2)*39/combin(50,3))*(9/47) = 2,096%.
Väri riverin jälkeen: (combin(11,2)*combin(39,2)/combin(50,4))*(9/46) = 3,462 %.
Eri maata olevilla taskukorteilla:
Väri flopin jälkeen: 0%
Väri vuoron jälkeen: 2*combin(12,4)/combin(50,4) = 0,430%.
Väri riverin jälkeen: (2*combin(12,3)*39/combin(50,4))*(9/46) = 1,458%.
Tässä ovat kommulatiiviset todennäköisyydet.
Suittien taskukorttien kanssa:
Väri flopilla: 0,842 %.
Väri vuorotellen: 2,937 %.
Joen huuhtelu: 6,400 %.
Eri maata olevilla taskukorteilla:
Väri flopilla: 0,000 %
Huuhtele vuorotellen: 0,430 %.
Joen huuhtelu: 1,888 %.
Hei velho, Ensinnäkin haluan sanoa, että rakastan antamiasi tarkkoja ja selkeitä vastauksia. Joka tapauksessa, jos Holdemissa taskukortit ovat AA ja floppikortit KQ9, mikä on todennäköisyys täydentyä täyskäteen? Olen työskennellyt tämän parissa iät ja ajat :( enkä vieläkään löydä vastausta, johon luottaisin.
Voit täydentää täyskäden ässällä ja K:lla, Q:lla tai 9:llä. Jäljellä on kaksi ässää ja kolme kutakin K:ta, Q:ta ja 9:ää. Tällaisia yhdistelmiä on siis 2 * 3 * 3 = 18. Ainoa muu vaihtoehto olisi K-, Q- tai 9-pari. Tällaisia yhdistelmiä on 3 * combin(3,2) = 9. Kaikkien yhdistelmien lukumäärä on 47 * 46 / 2 = 1081. Todennäköisyys on siis (18 + 9) / 1081 = 2,50 %.
Olen ollut valtava fani jo vuosia (jo ennen kuin sinä kiinnostuit pokerista ja urheiluvedonlyönnistä) ja odotin innolla jokaista Kysy velholta -kolumnia. On hienoa nähdä, että osallistut niihin taas! Kysymykseni kuuluu: paikallisessa korttihuoneessani he tarjoavat Aces Cracked, Win A Rack -peliä tiettyinä aikoina. Eli jos sinulla on taskuässät yhdessä heidän 3-6 tai 4-8 Texas Hold 'em -peleistään ja häviät potin, kasino antaa sinulle pelimerkkipakkauksen (100 dollaria). Yritän selvittää, kuinka usein a) saan taskuässät b) kuinka usein he häviäisivät, jos pelaisin niitä aggressiivisesti kuten minun pitäisi ja c) eikö olisi parempi vain sökätä koko pelin ja toivoa häviäväsi, koska 100 dollaria on yleensä parempi kuin mitä potti olisi ollut joka tapauksessa. Kaikki tilastot, jotka sinulla saattaa olla valmiina, olisivat upeita ja ikuisesti arvostettuja! Kiitos vielä kerran ja jatka massojen valaistamista!
Kiitos ystävällisistä sanoistasi. Todennäköisyys saada taskuässät yhdessä kädessä on 6/1326 eli kerran 221 kädessä. 10 pelaajan Texas Hold 'em -osiooni (/games/texas-hold-em/10players.html) mukaan taskuässävoiton todennäköisyys on 31,36 % olettaen, että kaikki pelaajat pysyvät mukana loppuun asti. Se on kuitenkin iso jos. Jos minun pitäisi arvata, arvioisin ässävoiton todennäköisyyden oikeassa 10 pelaajan pelissä olevan noin 70 %. Joten todennäköisyys saada taskuässä ja sitten hävitä on 0,3 * (1/221) = 0,1357 %. Joten 100 dollarilla per tapaus se on 13,57 senttiä per käsi. Yli kymmenen pelaajan kohdalla se maksaa pokerihuoneelle keskimäärin 1,36 dollaria per käsi, mikä leikkaa rakea melkoisesti. Olen taipuvainen olemaan samaa mieltä strategiastasi maksaa, joka pitää enemmän pelaajia kädessä ja lisää häviämismahdollisuuksiasi.
Ensinnäkin haluan kiittää teitä mahtavasta sivustosta. Nyt tässä on kysymykseni: Pelaamme Texas hold'emia ja floppaamme värinvedon kahdella pienellä kortilla. Me kaikki tiedämme värin saamisen prosentuaalisen todennäköisyyden. Mutta mitä todella haluamme, on käden voittoprosentti. Ja oletetaan, että olemme varmoja, että jollakulla on korkeampi kortti samaa maata kuin meillä. Joten kysymykseni kuuluu, mikä on prosenttiosuus siitä, että vain yksi kortti samaa maata näkyy eikä kaksi? Ystävällisin terveisin
Ole hyvä. Eli sinulla on neljä väriin ja flopin jälkeen kaksi pöydällä. Todennäköisyys saada tasan yksi vaaditusta maasta on 9 * 38 / yhdistelmä (47,2) = 342/1081 = 31,64 %.
Texas Hold'emissa haluaisin tietää todennäköisyyden sille, että jollekulle toiselle pelaajalle on jaettu kaksi samaa maata olevaa korttia muodostaakseen korkeamman värin kuin omani, kun riverillä on tasan kolme yhteiskorttia samasta maasta. Esimerkiksi jos minulla on pataa 89 ja yhteiskortteihin kuuluvat pata 37 ja pata K, pakassa on neljä pataa, jotka ovat suurempia kuin minun 9 (TJQA). Mikä on todennäköisyys, että jollekulle on jaettu käsi, jossa on kaksi pataa, joista ainakin yksi on suurempi (olettaen, että pelissä on 9)? Entä jos pataa on vain 2 (tai 3 tai x) suurempi kuin suurin taskukorttini? Kiitos avustasi ja upeasta sivustosta.
Seuraava taulukko näyttää todennäköisyyden 1–8 korkeammalle rankille ja 2–10 pelaajalle, sinut mukaan lukien. Esimerkissäsi, jossa on 4 korkeampaa rankkia ja yhteensä 9 pelaajaa, todennäköisyys on 16,45 %. Laskin nämä todennäköisyydet olettaen käsien välisen riippumattomuuden, mikä ei ole oikea oletus, mutta tulosten pitäisi olla lähellä todellisuutta.
Korkeamman värin todennäköisyysKorkeammat sijoitukset (alaspäin) pelaajien kokonaismäärän mukaan (kaikkialla)Ohjatun arvion
| Korkeammat arvot | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0,71 % | 1,41 % | 2,11 % | 2,80 % | 3,49 % | 4,17 % | 4,85 % | 5,52 % | 6,19 % |
| 2 | 1,31 % | 2,61 % | 3,89 % | 5,15 % | 6,40 % | 7,62 % | 8,84 % | 10,03 % | 11,22 % |
| 3 | 1,82 % | 3,60 % | 5,36 % | 7,08 % | 8,77 % | 10,43 % | 12,05 % | 13,65 % | 15,22 % |
| 4 | 2,22 % | 4,40 % | 6,52 % | 8,60 % | 10,63 % | 12,61 % | 14,56 % | 16,45 % | 18,31 % |
| 5 | 2,53 % | 4,99 % | 7,39 % | 9,72 % | 12,00 % | 14,23 % | 16,39 % | 18,50 % | 20,56 % |
| 6 | 2,73 % | 5,38 % | 7,96 % | 10,47 % | 12,91 % | 15,29 % | 17,60 % | 19,85 % | 22,03 % |
| 7 | 2,83 % | 5,58 % | 8,25 % | 10,84 % | 13,36 % | 15,81 % | 18,20 % | 20,51 % | 22,76 % |
| 8 | 2,83 % | 5,58 % | 8,25 % | 10,84 % | 13,36 % | 15,81 % | 18,20 % | 20,51 % | 22,76 % |
Korkeamman värin todennäköisyysKorkeammat sijoitukset (alaspäin) pelaajien kokonaismäärän mukaan (kaikkialla)Miplet-simulaatio
| Korkeammat arvot | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0,69 % | 1,41 % | 2,12 % | 2,83 % | 3,54 % | 4,25 % | 4,96 % | 5,66 % | 6,36 % |
| 2 | 1,28 % | 2,60 % | 3,91 % | 5,21 % | 6,48 % | 7,77 % | 9,05 % | 10,31 % | 11,56 % |
| 3 | 1,79 % | 3,61 % | 5,41 % | 7,19 % | 8,92 % | 10,68 % | 12,41 % | 14,11 % | 15,79 % |
| 4 | 2,19 % | 4,40 % | 6,58 % | 8,75 % | 10,85 % | 12,94 % | 15,01 % | 17,04 % | 19,04 % |
| 5 | 2,50 % | 5,00 % | 7,47 % | 9,92 % | 12,28 % | 14,63 % | 16,94 % | 19,21 % | 21,43 % |
| 6 | 2,71 % | 5,40 % | 8,06 % | 10,69 % | 13,23 % | 15,74 % | 18,23 % | 20,65 % | 23,03 % |
| 7 | 2,81 % | 5,61 % | 8,36 % | 11,08 % | 13,70 % | 16,30 % | 18,86 % | 21,37 % | 23,82 % |
| 8 | 2,81 % | 5,61 % | 8,36 % | 11,08 % | 13,70 % | 16,30 % | 18,86 % | 21,37 % | 23,82 % |
Hieno sivusto. Kysyn tätä omasta tietämyksestäni. Pelasin neljän hengen Texas Hold'emia. Minulle jaettiin taskuässät. Sain kuningasvärisuoran riverillä. Mietin, mitkä ovat todennäköisyydet saada kuningasvärisuora riverillä ässillä alussa?
Kiitos. Olettaen, että kuningaskortti koostuu toisesta kahdesta ässästäsi, kuninkaallisen kortin saamisen tapoja riverillä on 2 * 46 = 92. Tämä olisi taskuässäsi olevien kahden maan ja lisäkortin 46 mahdollisuutta. Yhdistelmä (50,5) = 2 118 760 tapaa jakaa 5 korttia 50:stä. Todennäköisyys on siis 92/2 118 760 = 1/23 030.
Jos flopilla tulee kolme samaa maata eikä minulla ole floppiin sopivaa maata ja pöydässä on jäljellä kymmenen pelaajaa, mikä on todennäköisyys sille, että jollakulla on väri?
Todennäköisyys sille, että yksikin pelaaja saa värin, on combin (11,2) / combin (49,2) = 55/1176 = 4,68 %. Olettaen, että käsien välillä on riippumattomuus, mikä ei pidä paikkaansa, todennäköisyys sille, että yhdeksällä pelaajalla ei ole väriä, on (1 − 0,0468 %) 9 = 64,98 %. Joten todennäköisyys sille, että ainakin yksi pelaaja saa värin, on 1 - 0,6498 = 35,02 %. Tämä on vain nopea arvio. Jos tekisin satunnaissimulaation, uskon, että todennäköisyys olisi hieman suurempi käsien välisen riippuvuuden vuoksi.
Hyvä herra velho, olen viime aikoina yrittänyt laskea värin saamisen todennäköisyyttä Texas Hold'emissa, jos jaetaan kaksi samaa maata olevaa taskukorttia? Vastaukseni on jatkuvasti 5,8 %, mutta tämä vaikuttaa lopulta väärältä. Apuasi arvostetaan suuresti, kiitos.
Todennäköisyys saada värin, kun jaettavat kortit ovat täsmälleen kolme samaa maata kuin taskukorttisi, on combin (11,3) × combin (39,2) / combin (50,5) = 122265 / 2598960 = 0,057706. Todennäköisyys saada värin, kun jaettavat kortit ovat neljä muuta samaa maata kuin taskukortit, on combin (11,4) × combin (39,1) / combin (50,5) = 2145 / 2118760 = 0,001012. Todennäköisyys saada värin, kun jaettavat kortit ovat viisi muuta samaa maata kuin taskukortit, on combin (11,5) / combin (50,5) = 462 / 2118760 = 0,000218. Todennäköisyys saada värin pöydälle toisessa maassa on 3 × combin(13,5) / combin(50,5) = 3861 / 2118760 = 0,001822. Laske nämä kaikki yhteen ja saat 0,057706 + 0,001012 + 0,000218 + 0,001822 = 0,060759.
Mikä on todennäköisyys sille, että Texas Hold'Emissa nähdään "rikki pöytä"? Eli pöydällä on viisi korttia, joista ei ole paria, väriä eikä suoraa.
Viiden eri arvoasteen yhdistelmien lukumäärä pelilaudalla on combin (13,5)*4 5 = 1287 × 1024 = 1 317 888.
Todennäköisyys sille, että nämä viisi arvoa edustavat kolmea maata, kahta kahdesta ja yhtä yhdestä, on combin(4,2)*2*combin(5,2)*combin(3,2)=360. Combin(4,2) on niiden tapojen lukumäärä, joilla kaksi maata neljästä voidaan valita kahdesti esitetyistä maista. 2 on niiden tapojen lukumäärä, joilla kaksi maata voidaan valita kerran esitetty maa. Combin(5,2) on niiden tapojen lukumäärä, joilla kaksi maata viidestä voidaan valita ensimmäisestä kahdesta kortista koostuvasta maasta. 4 ja 5 on niiden tapojen lukumäärä, joilla kaksi maata jäljellä olevista kolmesta voidaan valita toisesta kahdesta kortista koostuvasta maasta.
Todennäköisyys sille, että nämä viisi arvoa edustavat neljää maata, yhtä kahdesta ja kolmea yhdestä, on 4 * combin(5,2) * 3 * 2 = 240. 4 on tapojen lukumäärä, joilla yksi maa neljästä voi valita kahdesti esitetyille maille. Combin(5,2) on tapojen lukumäärä, joilla kaksi arvoa viidestä voi valita kyseiselle kahden kortin maalle. 3 on tapojen lukumäärä, joilla yksi arvo jäljellä olevista kolmesta voi valita ensimmäisen kortin maan. 2 on tapojen lukumäärä, joilla yksi arvo kahdesta voi valita toisen kortin maan.
Neljä maata voidaan järjestää viidelle eri arvolle 4 5 =1024 tavalla.
Joten todennäköisyys sille, että samaa maata on enintään kaksi, on (360 + 240) / 10²⁴ = 600/10²⁴ = 58,59 %.
On olemassa combin(13,5)=1287 tapaa järjestää 5/13 arvoa. Tällaisten yhdistelmien lukumäärä, joissa mitkään kolme arvoa eivät ole viiden arvoalueen sisällä, on 79. Tähän ei ole helppoa kaavaa. Minun piti käydä läpi jokainen yhdistelmä. Joten todennäköisyys, että arvot ovat riittävän kaukana toisistaan, on 79/1287 = 6,14 %.
Joten rikkoutuneen laudan todennäköisyys on (1317888/2596960)*(600/1024)*(79/1287) = 1,825211%.
Minua on haastateltu rikkoutuneiden suorien lukumäärän suhteen. Tässä on lista kaikista 79 mahdollisesta.
| 2378Q 2378 tuhatta 2379Q 2379 tuhatta 237TQ 237TK 237JQ 237JK 237QK 2389 tuhatta 238TK 238JK 238QK 2479Q 2479 tuhatta 247TQ 247TK 247JQ 247JK 247QK | 2489 tuhatta 248TK 248JK 248QK 257TQ 257TK 257JQ 257JK 257QK 258TK 258JK 258QK 267JQ 267JK 267JA 267QK 267QA 267KA 268JK 268JA | 268QK 268QA 268KA 269JA 269QA 269KA 278QK 278QA 278KA 279QA 279KA 289KA 3489 tuhatta 348TK 348JK 348QK 358TK 358JK 358QK 368JK | 368JA 368QK 368QA 368KA 369JA 369QA 369KA 378QK 378QA 378KA 379QA 379KA 389KA 469JA 469QA 469KA 479QA 479KA 489KA |
Pelaan Texas Hold 'Emiä Caesars Indianassa. Heillä on Bad Beat Jackpot, jossa neljä tai parempi voittaa. Molempien pelaajien on pelattava molemmat taskukortit, ja kortteja on jaettava neljälle pelaajalle. Kysymykseni kuuluu, mikä on todennäköisyys sille, että jokin käsi on bad beat -käsi olettaen, että kaikki pelaajat jatkavat loppuun asti?
Uusi Bad Beat Jackpot -osioni osoittaa tällaisen bad beatin todennäköisyydeksi 10 pelaajan pelissä 0,0000108 eli noin 1:93 000.
Miksi Ultimate Texas Hold 'Emin tuottotaulukossasi suositellaan suurta korotusta kahden kortin käsille, joiden odotusarvo on negatiivinen? Esimerkiksi samaa maata olevalle K/2:lle.
Voitto 51,24 %
Häviö 44,82 %
Tasapeli 3,94 %
Pöytäni Ultimate Texas Hold 'Emissa osoittaa, että pelaajalla on etulyöntiasema pelipanoksessa (Play), mutta haitta alku- ja sokkopanoksissa (Ante). Tässä tapauksessa pelaajalla on huonot kertoimet alku- ja sokkopanoksissa (Blind). Hänen kertoimensa pelipanoksessa (Play) ovat kuitenkin suotuisat. Joten tekemällä maksimikorotuksen hän saa parhaan hyödyn yli 50 %:n voittomahdollisuudestaan. Kahden muun panoksen huonot kertoimet laskevat kokonaisarvon alle 50 %:n. Tämä arvo olisi vielä pienempi pienemmällä korotuksella.
Vuoden 2008 World Series of Pokerissa Motoyuki Mabuchin nelosässät kaatuivat Justin Phillipin kuningasvärisuoraan. Minulla on yksinkertainen kysymys tämän todennäköisyydestä. ESPN ja muut arvioivat sen olevan noin 1/2,7 miljardia. Minusta näyttää siltä, että he yksinkertaisesti ottivat julkaistut nelosten todennäköisyydet ja kertoivat ne kuningasvärisuoran todennäköisyydellä. Onko tämä oikea laskutapa?
Olen myös eri mieltä luvusta 1/2,7 miljardia. Kuten sanoit, he näyttivät laskevan todennäköisyydet erikseen kullekin pelaajalle, vain siinä tapauksessa, että molemmat pelaajat käyttävät molemmat taskukortit, ja kertovat ne. Tällä menetelmällä saan todennäköisyydeksi 0,000000000341101 eli noin 1/2,9 miljardia. Ehkä tuo 1/2,7 miljardia sisältää myös pyöristysvirheen korolle lisäämisen molempien pelaajien todennäköisyyksille. He ilmeisesti myös unohtivat kertoa todennäköisyyden kahdella, syistä, jotka selitän myöhemmin.
Neljä ässää voi hävitä kuningasvärisuoralle kolmella tavalla:
Tapaus 1: Toisella pelaajalla on kaksi kuningasvärisuoraan, toisella on kaksi ässää, ja pöydällä on kaksi muuta ässää, kaksi muuta korttia kuningasvärisuoraan ja mikä tahansa muu kortti.
Esimerkki:
Pelaaja 1:

Pelaaja 2:

Hallitus: 




Useimmissa pokerihuoneissa sekä voittajan että häviävän pelaajan on käytettävä molempia taskukorttejaan voidakseen voittaa bad beat -jackpotin. Tämän tyyppinen bad beat oli nähty myös videolla; itse asiassa nämä olivat täsmälleen samat kortit.
Tapaus 2: Toisella pelaajalla on kaksi kuningasvärisuoraan (TK), toisella on yksi ässä ja "tyhjä" kortti, ja pöydällä on muut kolme ässää ja kaksi muuta korttia kuningasvärisuoraan.
Esimerkki:
Pelaaja 1:

Pelaaja 2:

Hallitus: 




Tapaus 3: Toisella pelaajalla on yksi kuningasvärisuoraan (TK) ja tyhjä kortti, toisella on kaksi ässää, ja pöydällä on kaksi muuta ässää ja kolme muuta korttia kuningasvärisuoraan.
Esimerkki:
Pelaaja 1:

Pelaaja 2:

Hallitus: 




Seuraava taulukko näyttää yhdistelmien lukumäärän kussakin tapauksessa sekä pelaajille että pelilaudalle. Oikeassa alakulmassa olevassa solussa näkyy yhdistelmien kokonaismäärä 16 896.
Bad Beat -yhdistelmät
| Tapaus | Pelaaja 1 | Pelaaja 2 | Hallitus | Tuote |
|---|---|---|---|---|
| 1 | 24 | 3 | 44 | 3 168 |
| 2 | 24 | 132 | 1 | 3 168 |
| 3 | 704 | 3 | 1 | 2 112 |
| Kokonais | 8 448 |
Voisimme kuitenkin vaihtaa pelaajien kortit ja silti saada huonon voiton. Joten meidän pitäisi kertoa yhdistelmien määrä kahdella. Tämän perusteella hyväksyttävien yhdistelmien kokonaismäärä on 2 × 8 448 = 16 896.
Kahden pelaajan Texas Hold 'Emissa kaikkien yhdistelmien kokonaismäärä on combin (52,2) × combin(50,2) × combin(48,5) = 2 781 381 002 400. Joten todennäköisyys sille, että neljä ässää häviää kuningasvärisuoralle, on 8 448 / 2 781 381 002 400 = 0,0000000060747 eli noin 1:165 miljoonaa. Jopa yhden huonon lyönnin todennäköisyys on 1:439 miljoonaa. Yksinkertainen syy siihen, miksi kertoimet eivät ole yhtä suuret kuin videossa ilmoitetaan, on se, että kaksi kättä ovat päällekkäin ja jaettu ässä on kyseessä. Toisin sanoen nämä kaksi tapahtumaa korreloivat positiivisesti.
Olet täysin oikeassa, artikkelin Telling the Truth about New York Video Poker mukaan. Pelaajan lopputulos on todellakin ennalta määrätty. Riippumatta siitä, mitä kortteja pelaaja pitää, hän ei voi välttää kohtaloaan. Jos pelaaja yrittää tarkoituksella välttää kohtaloaan, peli käyttää suojelusenkeli-ominaisuutta korjatakseen pelaajan virheen. Olen täysin samaa mieltä kirjoittajan kanssa siitä, että tällaisten pelien tulisi varoittaa pelaajaa siitä, ettei hän pelaa oikeaa videopokeria, ja voittotaulukko on merkityksetön mittari pelaajan todellisille kertoimille. On myös huomattava, että tällaiset väärennetyt videopokeriautomaatit eivät rajoitu New Yorkiin.
Hei, olen seitsemäsluokkalainen Havaijilta. Teen tiedemessuilla projektia pokerista ja shufflesta. Käytän taulukoitasi Texas Hold 'Emin taskukäsien voittoprosentista pelaajien lukumäärän mukaan. Toivoin, että voisit vastata muutamaan kysymykseen, jotka auttaisivat minua projektissani:
- Miten keksit kaavioista löytyvät prosenttiluvut?
- Jos käytit tietokoneohjelmaa, miten kehitit sen ja kuinka kauan se kesti?
- Mainitsit, että aloitit Wizard of Oddsin harrastuksena. Muuttuiko kokeilutyyli sivustosi tunnetuksi tullessa? Miksi tai miksi ei?
- Kahden pelaajan pöytä tehtiin raa'alla voimalla toimivalla silmukkaohjelmalla, joka kävi läpi kaikki 1225 mahdollista vastustajan korttia ja 1 712 304 mahdollista yhteiskorttia. Kolmesta kahdeksaan pelaajaa pelaava silmukka olisi vienyt kohtuuttoman kauan, joten tein satunnaisen simulaation.
- Kirjoitan lähes kaikki ohjelmani C++:lla, mukaan lukien molemmat juuri mainitsemani ohjelmat. Loput ovat Javalla tai PERLillä. Olen enimmäkseen kopioinut ja liittänyt koodia muista pokeripohjaisista ohjelmista. Uuden koodin kirjoittaminen kestää vain noin päivän.
- Kyllä, aloitin sivustoni harrastuksena kesäkuussa 1997. Vasta tammikuussa 2000 otin vastaan mainoksia ja yritin tehdä siitä liiketoimintaa. Se on käynyt läpi kolme eri verkkotunnusta vuosien varrella. Näin se näytti toukokuussa 1999. Sivuston tarkoitus on aina pysynyt samana: matemaattisesti perustuvan uhkapelistrategian resurssi. Vuosien varrella olen vain lisännyt lisää pelejä ja materiaalia. Yksi kokeilu oli tarjota NFL-vihjeeni kaudelle 2005 , mikä oli täydellinen epäonnistuminen.
Hei velho. Luin Texas Hold 'Em -kysymyksesi ja huomasin, että laskit 59,85 %:n todennäköisyydeksi nähdä ässä tai kuningas pöydällä, jos kädessäsi on taskukuningattaret. Miten päädyit tuohon lukuun?
Pakassa on jäljellä 50 korttia, joista viiden kortin yhdistelmiä on combin (50,5) = 2 118 760. Näistä korteista 42 on 2-Q. Viiden kortin yhdistelmien lukumäärä 42:sta on combin(42,5) = 850 668. Todennäköisyys sille, ettei saa kuningasta tai ässää, on 850 668 / 2 118 760 = 40,15 %. Näin ollen todennäköisyys saada ainakin yksi ässä tai kuningas on 1 - 40,15 % = 59,85 %.
Vaihtoehtoinen laskutoimitus on 1 - pr(flopissa ensimmäinen kortti ei ole ässä tai kuningas) × pr(flopissa toinen kortti ei ole ässä tai kuningas) × pr(flopissa kolmas kortti ei ole ässä tai kuningas) × pr(flopissa neljäs kortti ei ole ässä tai kuningas) × pr(flopissa viides kortti ei ole ässä tai kuningas) = 1 - (42/50) × (41/49) × (40/48) × (39/47) × (38/46) = 59,85%.
Mitkä ovat todennäköisyyteni saada flopilla täsmälleen kaksi samaa maata olevaa korttia lisää, kun minulla on kaksi samaa maata olevaa korttia Texas Hold'emissa?
Kaksi samaa maata olevaa korttia saa combin (11,2)=55 tavalla ja eri maata olevan kortin 39 tavalla. Flopilla on yhteensä combin(50,3)=19 600 mahdollista korttiyhdistelmää. Todennäköisyys sille, että flopin jälkeen on tasan neljä ja värisuora, on 55 × 39 / 19 600 = 10,94 %.
Olin mukana nettipokerin kädessä ja haluaisin tietää todennäköisyydet sille:
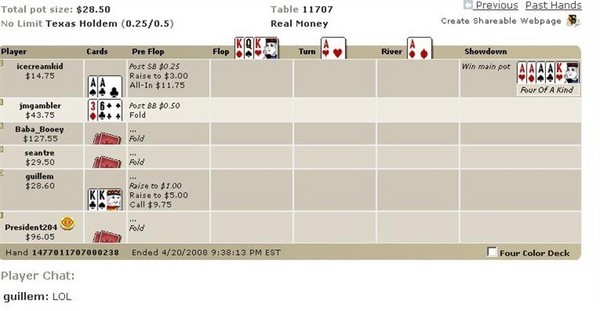
Normaalisti olen kyllästynyt bad beat -kysymyksiin, mutta tämä oli liian tuskallinen jätettäväksi huomiotta. Ennen ensimmäisen kortin jakamista todennäköisyys sille, että neljä kuningasta häviää neljälle ässälle kahden pelaajan pelissä, jossa molemmilla pelaajilla on taskuparit, on 2* combin (4,2)*combin(4,2)*44/(combin(52,2)*combin(50,2)*combin(48,5)) = 2*6*6*44/(1326*1225*1712304) = 1/877 961 175. Tämä oli kuuden pelaajan peli, joten combin(6,2) = 15 eri pelaajaparia. Kuuden pelaajan pelissä todennäköisyys on 15 kertaa suurempi eli 1/58 530 745. Kun ilmoitetut taskukortit on jaettu ja ennen floppia, todennäköisyys sille, että käsi päättyy näin, on 1/38 916.
Las Vegasilaisessa pelihuoneessa on käynnissä kampanja: Jos saat värin kaikissa neljässä maassa, saat 400 dollaria. Sinun on käytettävä molemmat taskukorttisi, ja aikaraja on viisi tuntia. Olettaen, että jakoja on 35 tunnissa ja että kello käynnistyy ensimmäisestä väristä, mikä on todennäköisyys saada kolme muuta väriä viiden tunnin sisällä? Kiitos.
Oletetaan, että ensimmäinen värisi on pata. 35 käden tuntitahtipelillä viidessä tunnissa voitaisiin pelata 175 kättä. Sinulla on sitten 175 kättä aikaa saada väri hertoissa, ruuduissa ja ristissä. Oletan, että pelaaja ei koskaan luovuta kättä, jolla on mahdollisuus saada väri yhdessä tarvitsemistaan maista.
Tietyn maan, esimerkiksi hertan, värin todennäköisyys molemmilla taskukorteilla on combin(13,2)×[combin(11,3)×combin(39,2) + combin(11,4)×39 + combin(11,5)]/(combin(52,2)×combin(50,5)) = 10576566/2809475760=0,003764605. Seuraavien 175 käden aikana herttavärin epäonnistumisen todennäköisyys olisi (1 - 0,003764605) 175 = 0,51682599.
Olisi väärin sanoa, että todennäköisyys sille, ettei kolmea muuta maata saada, olisi pr(ei hertta- tai ruutuväri) + pr(ei ruutua eikä ristiväri), koska silloin kahden maan saamisen todennäköisyys laskisi kaksinkertaiseksi. Joten sinun pitäisi lisätä takaisin pr(ei hertta- tai ruutuväri) + pr(ei hertta- tai ristiväri) + pr(ei risti- tai ruutuväri). Se kuitenkin vähentäisi virheellisesti kaikkien kolmen värin saamatta jäämisen todennäköisyyden liikaa. Joten sinun pitäisi lisätä takaisin pr(ei risti-, ruutu- tai herttaväri).
Todennäköisyys sille, että 175 kättä pelataan ilman, että kumpaakaan kahdesta tietystä maasta saadaan, on (1 - 2 × 0,003764605) 175 = 0,266442448.
Todennäköisyys sille, että 175 kättä pelataan eikä yhtäkään jäljellä olevista kolmesta maasta saada, on (1 - 3 × 0,003764605) 175 = 0,137015266.
Joten vastaus on 1 - 3 × 0,51682599 + 3 × 0,266442448 - 0,137015266 = 0,111834108.
Haluan kiittää dwheatleyta hänen avustaan tämän ongelman kanssa. Siitä keskustellaan ilmoitustaulullani Wizard of Vegasissa .
Doyle Brunson voitti kuuluisasti World Series of Pokerin päätapahtuman sekä vuosina 1976 että 1977. Molemmilla kerroilla hänellä oli taskukortteinaan 10-2, ja molemmilla kerroilla hän sai täyskäden riverillä. Mitkä ovat tämän todennäköisyydet?
Kahdella eriarvoisella kortilla täyskäden saamisen todennäköisyys on 1:121,6. Todennäköisyys saada se riverillä on 1:207.
Todennäköisyys saada tällainen käsi riverillä kahdesti kahdesta on 1:43 006.
Todennäköisyys sille, että tämä tapahtuu samoilla kahdella aloituskortilla, pelkästään arvojärjestyksessä, on 1/3 564 161.
Todennäköisyys sille, että tämä tapahtuu tasan 10-2 molemmilla kerroilla, on 1/295 379 826.
Palasin juuri VFW:n pokeriillasta. Sain kolme kertaa peräkkäin tuloksen 6-6! Näin ei ole koskaan ennen käynyt. Mitkä ovat todennäköisyydet saada sama taskupari kolme kertaa peräkkäin samana iltana? Voit olettaa, että ilta koostuu yhteensä 120 kierroksesta.
Vastaus ja ratkaisu löytyvät seuraavasta spoileritunnisteesta.
[spoileri]Voit olla millä tahansa hetkellä neljässä mahdollisessa tilassa:
- Tila 1: Ensimmäinen käsi tai mikä tahansa käsi, jossa viimeinen käsi ei ollut taskupari.
- Tilanne 2: Viimeinen käsi oli taskupari.
- Tilanne 3: Kaksi viimeistä kättä olivat samat taskuparit.
- Tilanne 4: Kolme samanlaista taskuparia peräkkäin on jo saavutettu.
Jos olet tilassa 1, voit edetä tilaan 2 todennäköisyydellä 3/51. Muuten pysyt tilassa 1.
Jos olet tilassa 2, voit edetä tilaan 3 todennäköisyydellä (4/52) × (3/51). Muussa tapauksessa palaat tilaan 1.
Jos olet tilassa 3, voit edetä tilaan 4 todennäköisyydellä (4/52) × (3/51). Muussa tapauksessa palaat tilaan 1.
Jos olet osavaltiossa 4, pysyt siellä.
Voit kuitenkin luoda siirtymämatriisin T seuraavasti:
| 0,941176 | 0,058824 | 0.000000 | 0.000000 |
| 0,941176 | 0,054299 | 0,004525 | 0.000000 |
| 0,941176 | 0,054299 | 0.000000 | 0,004525 |
| 0.000000 | 0.000000 | 0.000000 | 1.000000 |
Yhteensä pelattuja käsiä on 120, joten lasketaan T^120.
| 0,941044 | 0,058549 | 0,000265 | 0,000141 |
| 0,941025 | 0,058548 | 0,000265 | 0,000162 |
| 0,936786 | 0,058284 | 0,000264 | 0,004666 |
| 0.000000 | 0.000000 | 0.000000 | 1.000000 |
Oikeassa yläkulmassa oleva solu näyttää todennäköisyyden sille, että tilasta 1 aloittaminen johtaa meidät tilaan 4 120 aloituskäden jälkeen kolmen käden sekvenssissä, eli todennäköisyys on 0,000141471.
Otetaan tuon luvun käänteisluku, todennäköisyys on 1/7068,605131.
[/spoiler]Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .
Elokuvassa Casino Royale pokeriturnauksen viimeisessä kädessä neljällä pelaajalla on seuraavat kädet:
- Huuhtele
- Täyskäsi
- Täysi talo (eri arvoinen kuin ensimmäinen)
- Värisuora
Mikä on sen todennäköisyys?
Minun piti suorittaa simulaatio tätä varten. Simulaatiossani oletan, ettei kukaan koskaan luovuta. Lähes 2,2 miljardin kierroksen aikana tämä tapahtui 312 kertaa. Tämä vastaa noin yhden seitsemästä miljoonasta todennäköisyyttä.


