PEMDAS-säännön soveltaminen.

Jos olet minun kaltaiseni, saat Facebook-livessäsi loputtoman määrän toimintajärjestyskysymyksiä. Kaikkia niitä seuraa satoja vastauksia kommenteissa, joissa suurin osa ihmisistä on väärässä. Niiden ihmisten määrä, jotka koskaan myöntävät olleensa väärässä, on poikkeuksetta nolla.

Mikä tekee mielipiteestäni oikean? Ensinnäkin, jos saan kehua, haluaisin ajatella, että minut tunnustetaan johtavaksi kasinopelien matematiikan lähteeksi. Hae mitä tahansa kasinopeliä tai termiä, niin näet nimeni kaikkialla. Sen lisäksi minulla on matematiikan ja taloustieteen tutkinto Kalifornian yliopistosta Santa Barbarasta ja olen eläkkeellä oleva aktuaariyhdistyksen jäsen. Kaikki, mitä olen tehnyt yliopistosta valmistumiseni jälkeen, on ollut luonteeltaan matemaattista.

Esimerkki tällaisesta kysymyksestä on:

6 ÷ 2 (1 + 2) = ?

Pysähdy hetkeksi ja selvitä asia.

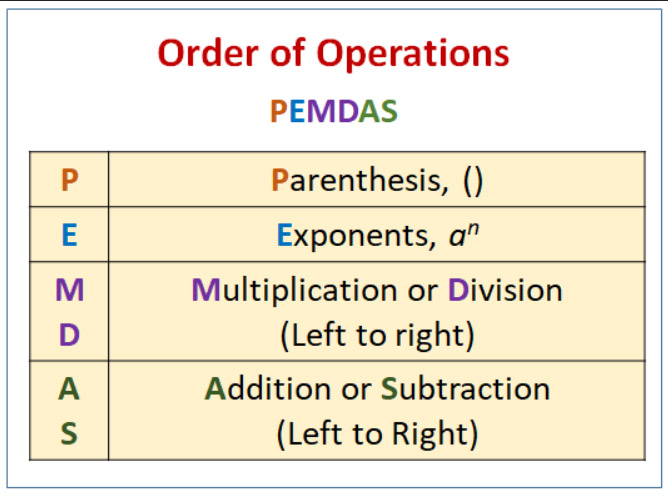
Jos sait vastaukseksi 1, olet väärässä. Epäilen sinun olevan väärässä, koska noudatat PEMDAS-nyrkkisääntöä laskutoimitusten järjestyksestä. Tämä on muistiväline, jota opetetaan noin viidennellä luokalla. Yksi tapa muistaa se, jonka minulle opetettiin, on "Anteeksi, rakas Sally-tätini". Sen tarkoituksena on opettaa lapsille lausekkeen laskemista seuraavassa järjestyksessä:

1. 1. Sulkeet
2. 2. Eksponentit
3. 3. Kertolasku
4. 4. Jako
5. 5. Aritmetiikka
6. 6. Vähennyslasku

Lukionopettajasi luultavasti todella uskoi tämän olevan oikein. Se ei kuitenkaan ole. En tiedä, mistä se sai alkunsa, mutta epäilen, että se on yksinkertaistettu muistilaite, jonka 10-vuotiaat lapset ymmärtävät helposti. Ongelmana yksinkertaistamisessa on se, että vaikka se voi useimmiten johtaa oikeaan vastaukseen, sääntöön on usein poikkeuksia. PEMDAS-menetelmän tapauksessa se johtaisi jonkun ratkaisemaan aiemmin mainitun 6 ÷ 2 (1 + 2) -ongelman seuraavasti:

1. 6 ÷ 2 (1 + 2) = 6 ÷ 2 (3) , koska ensin lasketaan sulkujen arvot
2. 6 ÷ 2 (3) = 6 ÷ 2 × 3, koska mikään operaattori sulkeiden ulkopuolella ei tarkoita kertolaskua
3. 6 ÷ 2 × 3 = 6 ÷ 6 , koska kertolasku tehdään ennen jakolaskua PEMDAS-laskennan mukaan
4. 6 ÷ 6 = 1

Yllä olevan logiikan virhe on kolmannessa vaiheessa. Kertolasku ei aina tapahdu ennen jakolaskua. Ne ovat yhtä tärkeitä. Kun molemmat esiintyvät samassa lausekkeessa, tee ensin vasemmalla kauimpana oleva.

Lisäisin vielä, että yhteenlaskun ei välttämättä tarvitse tapahtua ennen vähennyslaskua. Nekin ovat tasavertaisia. Kuitenkin yhteen- ja vähennyslaskun tapauksessa, joissa korkeammat säännöt eivät päde, sillä ei ole väliä, kumman teet ensin.

Tässä on oikea tapa laskea 6 ÷ 2 (1 + 2):

1. 6 ÷ 2 (1 + 2) = 6 ÷ 2 (3) , koska ensin lasketaan sulkujen arvot
2. 6 ÷ 2 (3) = 6 ÷ 2 × 3, koska mikään operaattori sulkeiden ulkopuolella ei tarkoita kertolaskua
3. 6 ÷ 2 × 3 = 3 × 3 , koska sekä kerto- että jakolaskussa lasketaan ensin vasemmalta
4. 3 × 3 = 9

Tässäpä sinulle toinen kysymys:

7 + 7 ÷ 7 + 7 × 7 – 7 = ?

Facebookissa vastaukseksi annetaan 56. Tämä on yksi niistä, jotka ihmiset erehtyvät, ei PEMDASin takia, vaan koska "laskimeni sanoi vastauksen olevan 56". Tämä on laiska ja väärä vastaus niiden antamina, jotka vain menevät vasemmalta oikealle. Väärä päättely on:

1. 7 + 7 ÷ 7 + 7 × 7 – 7 = 14 ÷ 7 + 7 × 7 – 7 , koska lasketaan ensin vasemmalta
2. 14 ÷ 7 + 7 × 7 – 7 = 2 + 7 × 7 – 7 , koska lasketaan ensin vasemmalta
3. 2 + 7 × 7 – 7 = 9 × 7 – 7 , koska lasketaan ensin vasemmalta
4. 9 × 7 – 7 = 63 – 7 , koska lasketaan ensin vasemmalta
5. 63 – 7 = 56

Oikea tapa arvioida tätä on:

1. 7 + 7 ÷ 7 + 7 × 7 – 7 = 7 + 1 + 7 × 7 – 7 , koska jakolasku on edellä yhteenlaskua ja on kertolaskun vasemmalla puolella
2. 7 + 1 + 7 × 7 – 7 = 7 + 1 + 49 – 7 , koska kertolasku on edellä yhteen- ja vähennyslaskua
3. 7 + 1 + 49 – 7 = 8 + 49 – 7 , koska yhteen- ja vähennyslaskun välillä tee ensin vasemmanpuoleisin laskutoimitus
4. 8 + 49 – 7 = 57 – 7 , koska yhteen- ja vähennyslaskun välillä tehdään vasemmanpuoleisin laskutoimitus ensin
5. 57 – 7 = 50

Huomaa, että tässä PEMDAS tekee oikein. Ihmiset tekevät virheitä, koska he eivät käytä laskimiaan oikein. On ratkaisevan tärkeää syöttää numerot ja laskutoimitukset oikeaan järjestykseen. Tämä on paljon helpompaa tehdä laskimilla, jotka käyttävät käänteistä puolalaista merkintätapaa, kuten HP15C. Muuten, jokainen, jolla on HP15C tai 12C, on heti ystäväni.

Lopuksi haluaisin lisätä oman vivahteeni näihin laskutoimitusten järjestys -pulmiin tällä itse luomallani pulmalla, sekä sen logiikan että asettelun osalta. Myönnän, että varastin kuvat Googlesta. Tämä pulma on saanut inspiraationsa samankaltaisesta, mutta vielä vaikeammasta pulmasta Mind Your Decisions YouTube -kanavalta. Ole hyvä ja julkaise se itse minne haluat; toivon, että se leviää kulovalkean tavoin.

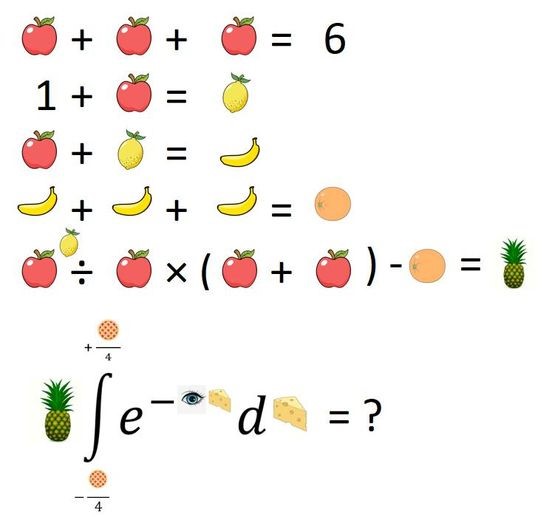
Osapisteet pelkän ananaksen ratkaisemisesta ja täydet pisteet integraalin ratkaisemisesta.

Julkaisen vastaukset 29. kesäkuuta ilmestyvässä uutiskirjeessä. Siihen asti toivottavasti kaikki on hyvin.

Kirjoittanut: Michael Shackleford