WOO logo

Velho suosittelee

Taitettu suorakulmiopalapeli


Tässä uutiskirjeessä esittelen matemaattisen pulman Mensa Bulletinin marraskuun numerosta.

Tarkastellaan 1x4-kokoista suorakulmiota. Taita nyt suorakulmio niin, että vastakkaiset kulmat menevät päällekkäin, kuten tässä kaaviossa.

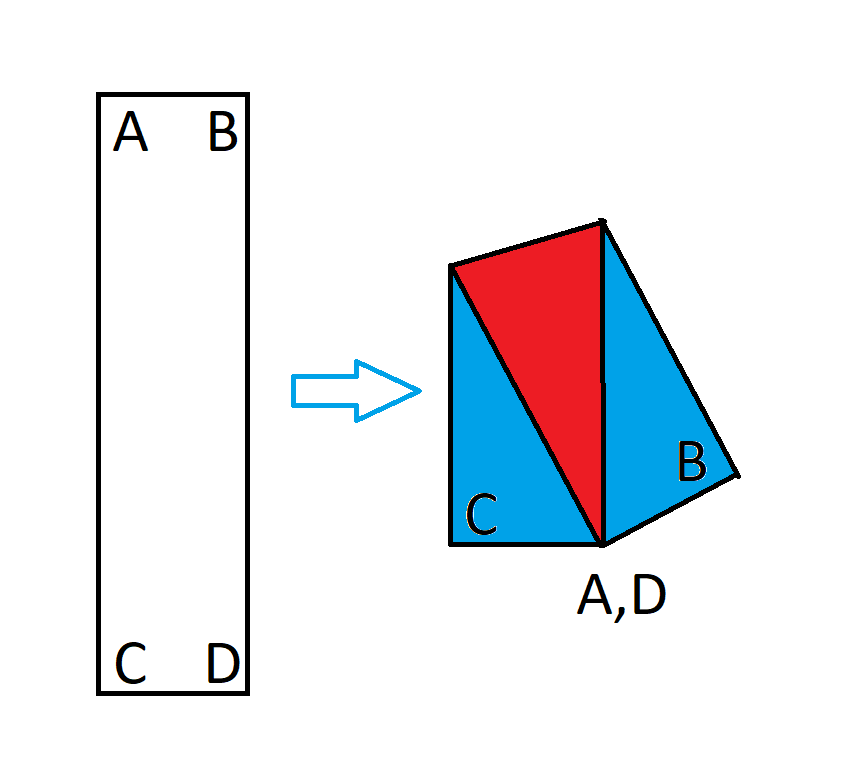
1x4 suorakulmio

Taitettuaan suorakulmion siitä muodostuu epäsäännöllinen viisikulmio. Mikä on viisikulmion sen osan suhde, jossa paperi menee päällekkäin, kokonaispinta-alaan? Toisin sanoen, yllä olevan kuvan punaisen alueen suhde kokonaispinta-alaan.

Vieritä alaspäin nähdäksesi vastauksen ja ratkaisun.

Vastaus

Vastaus on 17/47 = noin 0,3617

Ratkaisu

Selitän ratkaisua määrittelemällä lisää pisteitä, kuten seuraavasta kuvasta näkyy. F on E:n ja G:n keskipiste.

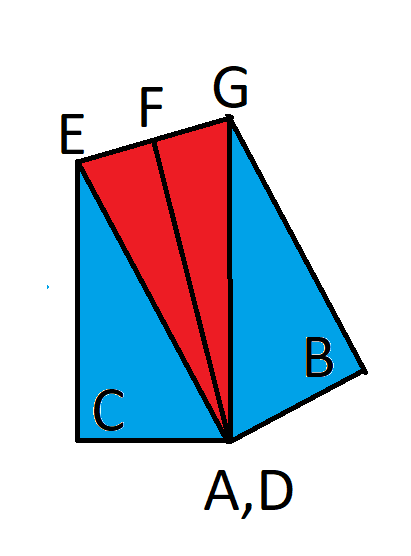
1x4 suorakulmio, viisikulmio - ratkaisu

Tiedämme:

Vaihtovirta = 1

CE + AE = 4

Ratkaistaan AE Pythagoraan lauseen avulla:

1 2 + (CE) 2 = (AE) 2

Sijoittamalla AE:n numerolla 4 – CE saadaan:

1 2 + (CE) 2 = (4 – CE) 2

1 + (CE) 2 = 16 – 8 (CE) + (CE) 2

8(CE) = 15

CE = 15/8

Palataksemme kaavaan 1 2 + (CE) 2 = (AE) 2 , voimme ratkaista (AE):n, koska tunnemme EC:n:

(AE) ² = (CE) ² + 1²

(AE) 2 = (15/8) 2 + 1 2

(AE) 2 = 225/64 + 64/64

(AE) 2 = 289/64

AE = 17/8

Ennen taittoa pituus A:sta D:hen oli suorakulmion lävistäjä. Käyttämällä Pythagoraan kaavaa saadaan pituus sqrt(17).

(AF) on puolet tuosta pituudesta eli neliö(17)/2.

Tietäen AE:n ja AF:n, voimme ratkaista EF:n käyttämällä jälleen Pythagoraan lauseketta:

(AE) ² = (EF) ² + (AF) ²

(17/8) 2 = (EF) 2 + (sqrt(17)/2) 2

289/64 = (EF) 2 + 17/4

289/64 = (EF) 2 + 272/64

(EF) 2 = 17/64

EF = neliöjuuri(17)/8

Kuten aiemmin todettiin, F on E:n ja G:n keskipiste. Tämä EG = 2 * neliö(17) / 8 = neliö(17) / 4.

Punainen kolmio, AEG = (1/2) × pohja × korkeus =

= (1/2) × neliö (17/4) × neliö (17)/2

= (1/2) × (17/8) = 17/16

Kolmion ACE pinta-ala = (1/2) * pohja * korkeus =

(1/2) × 1 × (15/8) = 15/16.

Koko viisikulmion pinta-ala = AEG + 2*ACE =

(17/16) + 2 * (15/16) = 47/16

Näin ollen punaisen alueen pinta-ala koko viisikulmioon nähden =

(17/16) / (47/16) = 17/47 = noin 0,3617


Kirjoittanut: Michael Shackleford