Jaollisuuden 3:lla todistus

Tällä viikolla aion pitää taukoa presidentinvaaleihin liittyvästä tietokilpailusta ja kokeilla jotain uutta. Olen aina nauttinut hyvistä matemaattisista todistusaineistoista. Kunnes ideani loppuvat, käyn läpi joitakin kuuluisia matemaattisia lauseita ja yritän selittää mahdollisimman helposti ymmärrettävästi, miksi ne ovat totta. Aluksi osoitan tällä viikolla, että jos minkä tahansa kokonaisluvun numeroiden summa on jaollinen kolmella, niin kokonaisluku on jaollinen kolmella. Ennen kuin pääsemme siihen, esittelen kuitenkin tavanomaisen viikoittaisen logiikkapulman.

Logiikkapulma

Pöydällä on neljä korttia. Kuvapuoli ylöspäin olevat kortit on merkitty numeroilla D, K, 3 ja 7. Tiedät, että jokaisessa kortissa on toisella puolella kirjain ja toisella numero. On olemassa valmistussääntö, jonka mukaan kortissa, jossa on toisella puolella D, on oltava toisella puolella numero 3. Mitkä kaksi korttia sinun on käännettävä varmistaaksesi, että tätä sääntöä on noudatettu?

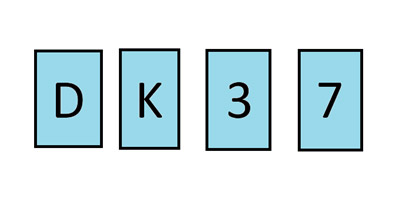
Vastaus tulee uutiskirjeen loppuun.

Jaollisuuden 3:lla todistus

Kuten johdannossa todettiin, kokonaisluvun jaollisuutta kolmella voidaan testata seuraavasti:

1. Ota numeroiden summa.
2. Jos säännön 1 summa on tasan jaollinen kolmella, niin alkuperäinen luku on myös. Samoin jos summa ei ole jaollinen kolmella, niin alkuperäinenkään luku ei ole.

Katsotaanpa esimerkiksi Valkoisen talon puhelinnumeroa, joka on 2024567041. Numeroiden summa on 2 + 0 + 2 + 4 + 5 + 6 + 7 + 0 + 4 + 1 = 31. Luku 31 ei ole jaollinen kolmella, joten alkuperäinen lukukaan ei ole.

Todistaaksesi tämän toimivuuden, jaa alkuperäinen luku seuraavasti:

6; fonttiperhe: 'Open Sans', sans-serif; väri: #313131 !tärkeä; ">2024567041 = (2*1000000000) + 0 + (2*10000000) + (4*1000000) + (5*100000) + (7*1000) + 0 + (4*10) + (1*1)

Seuraavaksi erota luvun 10 potenssit kahteen osaan, ykköseen ja muuhun osaan:

= (2*(999999999+1)) + 0 + (2*(9999999+1)) + (4*(999999+1)) + (5*(99999+1)) + (7*(9999+1)) + 0 + (4*(9+1)) + (1*(0+1))

On selvää, että mikä tahansa luku, jossa on pelkkiä yhdeksiköitä, on tasan jaollinen molemmilla kolmella. Esimerkiksi 99999 = 3 * 33333.

Siitä huolimatta, järjestetään yllä olevan numeron termit uudelleen.

= (2*999999999) + (2*9999999) + (4*999999) + (5*99999) + (7*9999) + (4*9) + (1*0) + (2*1) + (2*1) + (4*1) + (5*1) + (7*1) + (4*1) + (1*1)

Jokainen seitsemän ensimmäisen termin joukossa oleva termi on ilmeisesti tasan jaollinen kolmella, koska ne jakavat tasan luvulla, jossa on kaikki 9. Toisin sanoen, (2*999999999) + (2*9999999) + (4*999999) + (5*99999) + (7*9999) + (4*9) + (1*0) on tasan jaollinen 9:llä, joten voimme poistaa tuon osan. Jäljelle jää:

(2*1) + (2*1) + (4*1) + (5*1) + (7*1) + (4*1) + (1*1) = 2+0+2+4+5+6+7+0+4+1 = 31

Tämä on numeroiden summa, joka on 31. Koska tämä jäljelle jäävä osa ei jaa tasan kolmella, koko lukukaan ei voi jakaa tasan kolmella.

Samaa sääntöä voidaan käyttää myös jaollisuuden testaamiseen luvulla 9. Jos alkuperäisen luvun numeroiden summa on jaollinen luvulla 9, niin on myös koko luku. Myös päinvastoin pätee: jos numeroiden summa ei ole tasan jaollinen luvulla 9, niin koko lukukaan ei ole jaollinen.

Logiikkapulman ratkaisu

Kutsutaan sääntöä, jonka mukaan luvun 3 on oltava D-säännön vastakkaisella puolella, "D-3"-säännöksi.

1. • On selvää, että meidän on käännettävä D-kortti varmistaaksemme, että toisella puolella on 3.
2. • K-kortin toisella puolella on oltava numero.Koska vastapuolella ei voi olla D:tä, tämä kortti ei auta meitä todistamaan, ettei D-3-sääntöä noudatettu.
3. • Kortin 3 toisella puolella täytyy olla kirjain. Jos kyseinen kirjain on D, se tukee D-3-sääntöä. Jos toisella puolella on jokin muu kirjain, se ei auta meitä. Joten joko tämä kortti noudattaa D-3-sääntöä tai se ei ole relevantti. Joka tapauksessa etsimme korttia, joka rikkoo sääntöä ja mitätöi D-3-säännön. Toisella puolella oleva kirjain ei kumoa D-3-sääntöä. Joten sitä ei tarvitse tarkistaa.
4. • Kortin 7 toisella puolella täytyy olla kirjain. Jos kyseinen kirjain olisi D, kortti kumoaisi D-3-säännön. Joten on tarkistettava, ettei kyseessä ole D-7-kortti, mikä olisi D-3-väitteen supistaminen.

Näin ollen vain D- ja 7-kortit on tarkistettava.