Velho suosittelee
-
[VAL]11000 tervetuliaisbonus -
[VAL]3000 tervetuliaisbonus -
JOPA $777 BONUS
Eulerin identiteetti
Tällä viikolla otamme vastaan ison haasteen, todistamme Eulerin identiteetin. Jos olet unohtanut, se on kenties matematiikan kaunein identiteetti: eπi +1 = 0. Rakastan tätä identiteettiä niin paljon, että se on käyntikortissani ja saatan jopa ottaa siitä tatuoinnin. Ennen kuin pääsemme siihen, esittelen kuitenkin tavanomaisen viikoittaisen logiikkapulman.
Logiikkapulma
Sinulla on neljä ketjua, joissa kussakin on kolme lenkkiä. Kuinka voit yhdistää ne kaikki yhteen muodostaaksesi ympyränmuotoisen silmukan, jossa on kaikki 12 lenkkiä, leikkaamalla vain kolme lenkkiä?
Eulerin identiteetin todistaminen
Yksi matematiikan kuuluisimmista yhtälöistä on Eulerin identiteetti, joka sanoo e πi +1 = 0. Hämmästyttävää siinä on se, että se yhdistää matematiikan viisi tärkeintä lukua: 0, 1, e, π ja i.
Ratkaisuni vaatii Taylorin laajennuksen kaavan tuntemisen. Muistutuksena, se on:
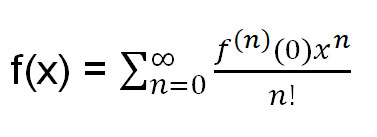
Missä f (n) (0) = funktion f(x) n:s derivaatta, joka on laskettu kohdasta 0.
Henkilökohtaisesti pidän yhtälöä yhtenä hämmästyttävimmistä ja kauneimmista koko matematiikassa. Minulle se on todiste siitä, että matematiikassa on jotain jumalallista.
Tässä on kuitenkin kolme Taylorin laajennusta yleisiin funktioihin, joita tarvitsemme:
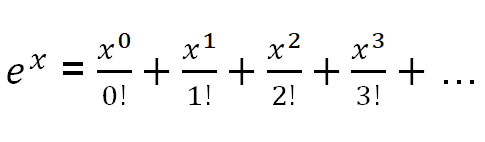
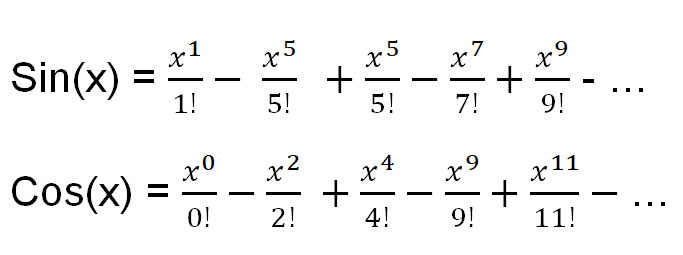
Käytetään funktion e x Taylorin laajennusta e πi:n löytämiseen.
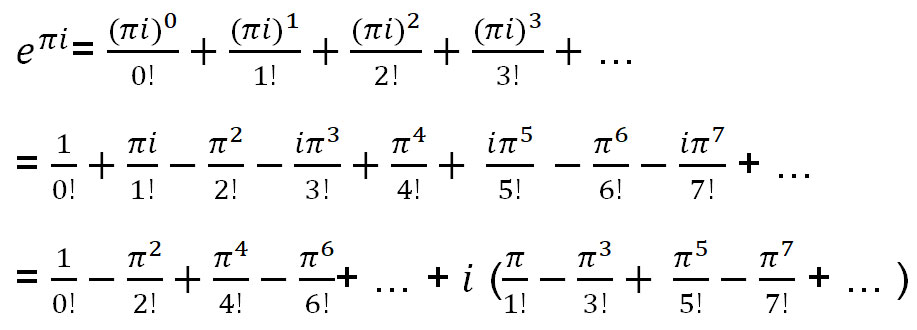
Yllä oleva yhtälö voidaan ilmaista sin(x):n ja cos(x):n funktiona:
= cos(π) + i × sin(π)
= -1 + i ×0
= -1
Joten meillä on e πi = -1. Tämä voidaan järjestää uudelleen tavalliseen muotoon:
eπi +1 = 0
Logiikkapulman ratkaisu
- Ota yksi neljästä ketjusta ja avaa ja erota kaikki kolme lenkkiä. Kutsu kolmea muuta ketjua 1, 2 ja 3.
- Yhdistä ketjut 1 ja 2 yhdellä lenkillä, jolloin saat seitsemän lenkin ketjun.
- Yhdistä vaiheen 2 seitsemänlenkkinen ketju ketjuun 3 toisella lenkillä, jolloin saat 11-lenkkisen ketjun.
- Yhdistä vaiheen 3 11-lenkkisen ketjun kaksi päätä viimeisellä lenkillä luodaksesi 12-lenkkisen ympyrän.