Kuinka pelata shakin luokitussääntöjä

Tällä viikolla tarkastelemme tapaa, jolla voit parantaa pelisi shakkiarvostelukaavaa parantamatta peliäsi lainkaan. On syytä varoittaa, että kyseessä on vain pieni etu ja pääasiassa akateemista mielenkiintoa. Ennen sitä esittelen kuitenkin, kuten tavallista, viikoittaisen logiikkapulmamme.

Logiikkapulma

Jonossa on 50 ihmistä, jotka on numeroitu järjestyksessä 1–50. Ensimmäinen henkilö jonossa on numero 1. Jokainen henkilö joko puhuu aina totta tai valehtelee aina. Kaikki tietävät kaikkien totuudenmukaisuuden.

Kaikki parilliset ihmiset sanovat: "Jokainen edessäni on valehtelija."

Kaikki parittomat sanovat: "Jokainen minun takanani on valehtelija."

Kuka puhuu totta?

Kuinka pelata shakin luokitussääntöjä

Yleisin shakin luokitusjärjestelmä on tietääkseni Elo-luokitusjärjestelmä. Se on nimetty Arphad Elon mukaan. Samaa järjestelmää käytetään myös muissa peleissä ja urheilulajeissa.

Pohjimmiltaan se toimii kaavalla, joka määrittää minkä tahansa pelaajan voittotodennäköisyyden molempien pelaajien luokituksen perusteella. Voittava pelaaja saa pisteitä suhteessa häviämisen todennäköisyyteen. Samoin häviävä pelaaja saa pisteitä suhteessa voittotodennäköisyyteen. Voitosta annetaan yksi piste, tasapelistä 0,5 ja tasapelistä 0.

Järjestelmä perustuu oletukseen, josta olen samaa mieltä, että pelaajan suoritusta voidaan mallintaa kellokäyrältä piirretyn satunnaisluvun perusteella, jossa pelaajan pisteytys on keskiarvo. Pelaaja, joka saa korkeamman luvun, voittaa.

Voiton todennäköisyys määritetään seuraavasti:

Olkoon r1 = pelaajan 1 luokitus.

Olkoon r2 = pelaajan 2 luokitus.

p = Todennäköisyys, että pelaaja 1 voittaa.

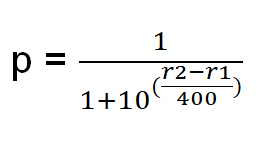
Katsotaanpa esimerkkiä. Olkoon r1=1900 ja r2=2000.

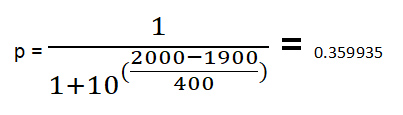
Olettaen, että voitosta annetaan 1 piste ja tappiosta 0 pistettä, luokituksen nousu on 32*(todelliset pisteet – voiton todennäköisyys).

Yllä olevassa esimerkissämme, jos pelaaja 1 häviää, kuten hänen ennustetaan tekevän, hänen luokituksensa laskee 11,52 pistettä ja pelaajan 2 luokitus nousee saman verran. Jos pelaaja 1 voittaa, hänen luokituksensa nousee 20,48 pistettä ja pelaajan 2 luokitus laskee saman verran.

Elo-järjestelmä perustuu suorituskyvyn keskihajontaan, joka on mallinnettu yllä kuvatulla satunnaislukumenetelmällä ja on arvo 200. Oletan tämän pitävän paikkansa. Voittotodennäköisyyden kaava, johon Elo-taulukot perustuvat, ei kuitenkaan ole yhdenmukainen tällaisen keskihajonnan kanssa, paitsi jos pistemääräero on 0 tai 189.

Oikea todennäköisyys sille, että pelaaja, jonka arvo on r1, voittaa, on:

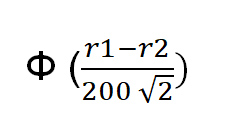
Missä funktio Φ(x) = todennäköisyys sille, että satunnainen standardinormaali muuttuja on pienempi kuin x. Excelissä oikea kaava on norm.s.dist((r1-r2)/(200*sqrt(2)),1).

Tarkastellaan tapausta, jossa luokitusten ero on 100. Tehdään pelaajasta 1 altavastaaja. Elo-kaavan mukaan pelaajalla 1 on 35,99 %:n voittomahdollisuus. Hänen todellinen todennäköisyytensä, joka perustuu suorituksen 200:n keskihajontaan, on kuitenkin 36,18 %. Toisin sanoen pelaajan 1 voitto on hyvä veto ja pelaajan 2 huono veto. Näytän, että pelaajan 1 odotettu luokitusnousu ja pelaajan 2 odotettu tappio on 0,06 pistettä.

Seuraavaksi tarkastellaan 300-pisteiden eroa, jossa pelaaja 1 on altavastaaja. Tässä Elo-kaava antaa pelaajalle 1 15,10 %:n voittomahdollisuuden, kun taas minä osoitan sen olevan 14,44 %. Tämä tekee pelin ottamisesta huonon valinnan pelaajalle 1 ja hyvän valinnan pelaajalle 2. Pelaajan 1 odotettu tappio on 0,21 pistettä, samoin kuin pelaajan 2 odotettu voitto.

Todellisten todennäköisyyksien taustalla oleva matematiikka perustuu Gaussin käyrään ja on monimutkaisempi kuin haluan tässä uutiskirjeessä käsitellä.

Lopputulos on, että jos erotus on yli 189, pelin voittaminen on hyvä veto suosikille. Samoin jos ero on alle 189, pelin voittaminen on hyvä veto altavastaajalle.

Vinouma on kuitenkin melko pieni. En hyväksyisi enkä hylkäisi pelejä tämän tiedon perusteella. Pikemminkin mielestäni sinun pitäisi valita mikä tahansa peli rakkaudesta shakkiin.

Lisätietoja: Wikipedian artikkeli Elo-luokitusjärjestelmästä.

Logiikkapulman vastaus

Henkilöt 2 ja 49 ovat ainoat, jotka puhuvat totta.

Logiikkapulman ratkaisu

Aloitetaan henkilöstä 1. Jos hän puhuu totta, kaikki muut valehtelevat. Henkilö 3 kuitenkin sanoo, että kaikki numerot 4–50 valehtelevat. Jos se on totta, henkilö 3 puhuu totta. Henkilö 1 kuitenkin sanoo valehtelevansa. Tämä johtaa ristiriitaan. Henkilön 1 täytyy siis valehdella.

Henkilö 2 sanoo vain, että henkilö 1 valehtelee. Tämä tekee henkilöstä 2 totuudenmukaisen.

Jokainen parillinen henkilö lukujen 4 ja 50 välillä sanoo, että henkilö 2 valehtelee. Se tekee heistä kaikista valehtelijoita.

Henkilö 49 sanoo, että henkilö 50 valehtelee, mikä on totta. Se tekee henkilöstä 49 totuudenmukaisen.

Jokainen pariton henkilö numeroiden 3 ja 47 välillä sanoo, että henkilö 49 valehtelee. Se tekee heistä kaikista valehtelijoita.

Näin ollen ainoat totuutta puhuvat ihmiset ovat numerot 2 ja 49.