WOO logo

Velho suosittelee

Piirretyn kulman lauseen todistus (osa 1)

Tällä viikolla palaamme matemaattisen lauseen todistamiseen. Tämän viikon teema on sisäänpiirretyn kulman teoreema. Tämä todistus on tavallista monimutkaisempi, joten jaan sen kahteen osaan, ja osa 2 on ensi viikolla. Ennen kuin pääsemme siihen, esittelen kuitenkin tavanomaisen viikoittaisen logiikkapulmani.

Logiikkapulma

Alla olevassa kaaviossa siirrä yhtä kolikkoa muodostaaksesi kaksi riviä, joissa kummassakin on neljä kolikkoa.

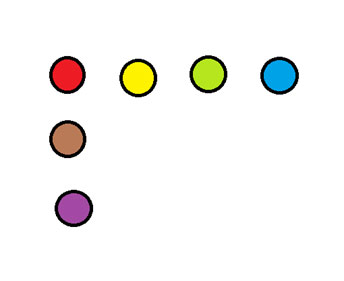
kaavio

Vastaus näkyy uutiskirjeen alareunassa.

Piirretyn kulman lauseen todistus (osa 1)

Ennen kuin selitän ympyrän sisään piirretyn kulman teoreeman, määrittelen joitakin ympyrän pisteitä seuraavassa kaaviossa.

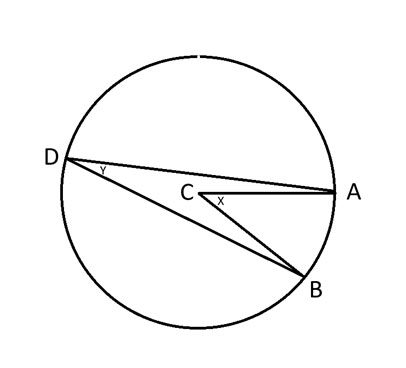
ympyrä

A, B ja D = Mitkä tahansa kolme pistettä ympyrällä.

C = Ympyrän keskipiste.

x = Kulma ACB.

y = Kulma ADB.

Piirretyn kulman teoreema sanoo, että kulma 2y = x.

Tässä uutiskirjeessä pyrin todistamaan sen erityistapauksessa, jossa AD tai BD muodostavat ympyrän halkaisijan. Ensi viikolla käsittelen tätä tarkemmin D:n sijainnin yleisessä tapauksessa.

Kutsutaan tapausta 1, jossa AD muodostaa ympyrän halkaisijan. Tässä on uusi kaavio kyseistä tapausta varten.

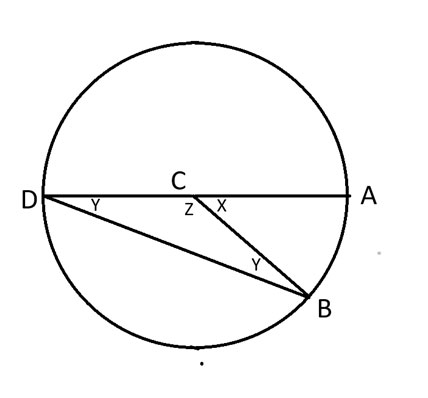
kaaviomainos

Yllä olevassa kaaviossa AD muodostaa ympyrän halkaisijan, jonka keskellä on C.

Voimme sanoa x + z = 180 astetta, koska ne muodostavat puolet ympyrän 360 asteen kokonaispituudesta.

BCD muodostaa tasakylkisen kolmion. Näin ollen kulma CDB = CBD = y.

Kuten 13. marraskuuta 2025 julkaisemassani uutiskirjeessä todistettiin, kolmion sisäkulmien summa on 180 astetta. Toisin sanoen z + 2y = 180 astetta.

Kirjoitetaanpa molemmat yhtälöt uudelleen:

z = 180 – x

z = 180 – 2y

Yhtälöidään ne molemmat, koska ne molemmat ovat yhtä suuret kuin z.

180 – x = 180 – 2y

-x = -2y

x = 2y.

Olemme siis todistaneet ympyrän sisään piirretyn kulman lauseen erityistapauksen, jossa kaksi ympyrän pistettä muodostaa halkaisijan. Ensi viikolla jatkamme tämän todistamista yleisessä tapauksessa.

Logiikkapulman ratkaisu

Siirrä sininen kolikko punaisen kolikon päälle. Alla olevassa kaaviossa numerot osoittavat kunkin pinon kolikoiden lukumäärän.

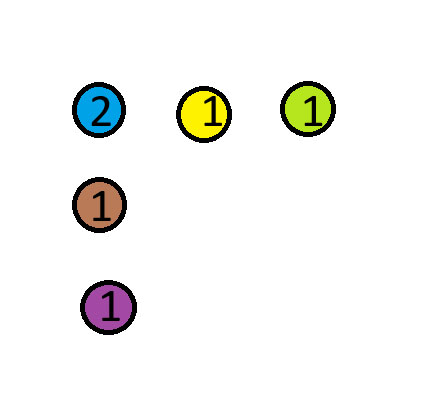
kolikot

Kuitutus: Sain tämän palapelin Mind Your Decisions YouTube -kanavalta. Tämä on palapeli nro 3 linkitetyssä videossa.