Piirretyn kulman lauseen todistus (osa 2)

Saatat muistaa, että viime viikolla aloitin sisäänkirjoitetun kulman teoreeman todistuksen. Tällä viikolla viimeistelemme sen. Ennen kuin pääsemme siihen, esittelen kuitenkin tavanomaisen viikoittaisen logiikkapulmani.

Logiikkapulma

Mitkä seuraavista väittämistä ovat totta?

1. Yksi näistä väitteistä on väärä.
2. Kaksi näistä väitteistä on vääriä.
3. Kolme näistä väitteistä on vääriä.
4. Neljä näistä väitteistä on vääriä.
5. Viisi näistä väitteistä on vääriä.
6. Kuusi näistä väitteistä on vääriä.
7. Seitsemän näistä väitteistä on vääriä.
8. Kahdeksan näistä väitteistä on vääriä.
9. Yhdeksän näistä väitteistä on väärin.
10. Kymmenen näistä väitteistä on vääriä.

Vastaus näkyy uutiskirjeen alareunassa.

Piirretyn kulman lause (osa 2)

Muistutan teitä siitä, mitä sisäänpiirretyn kulman teoreema sanoo.

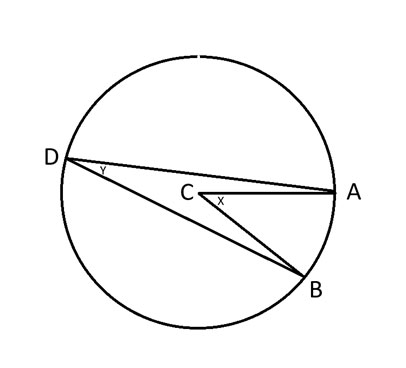
A, B ja D = Mitkä tahansa kolme pistettä ympyrällä.

C = Ympyrän keskipiste.

x = Kulma ACB.

y = Kulma ADB.

Piirretyn kulman teoreema sanoo, että kulma 2y = x.

Viime viikolla osoitin tämän pitävän paikkansa erityistapauksessa, jossa AD tai BD muodostavat ympyrän halkaisijan. Tällä viikolla käytän tätä osoittaakseni, että lause pitää paikkansa yleisessä tapauksessa D:lle.

Aion eritellä kaikki mahdolliset D:n sijainnit seuraavasti:

Tapaus 1 = AD tai BD muodostaa ympyrän halkaisijan (todistettu viime viikolla)

Tapaus 2 = D sijaitsee (vai "asettaako se"?) ympyrän kaaren suuntaisesti pisteistä A ja B vastakkaisella puolella.

Tapaus 3 = Kaikki muut

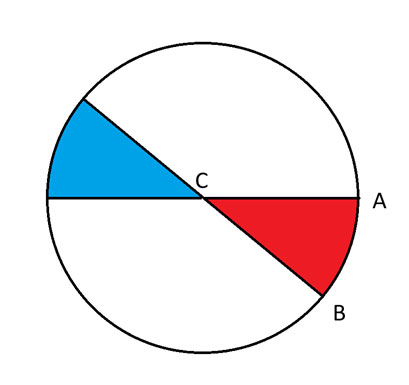
Toisin sanoen tapaus 2 kattaa tapaukset, joissa D on ympyrän reunalla sinisellä alueella. Tapaus 3 kattaa muut paikat kyseisen sinisen viipaleen ulkopuolella.

Käytetään keskustelussa seuraavaa kaaviota.

Olkoon:

x = x1 + x2

y = y1 + y2

z = z1 + z2

Pyrimme todistamaan, että x = 2y

Piirsin varovasti viivan D:stä C:hen, muodostaen ympyrän halkaisijan. Piste E on kohta, jossa se leikkaa ympyrän toisen sivun.

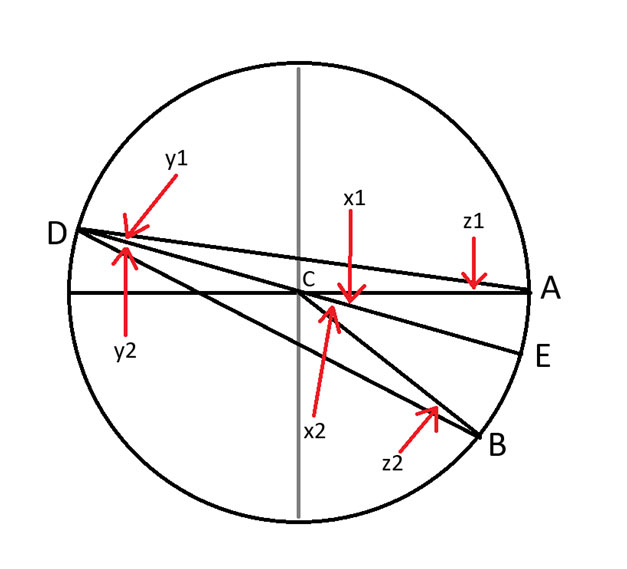
Kulmien numeroiden olisi pitänyt olla alaindeksissä, koska piirto-ohjelmistoni ei sallinut sitä.

Tarkastellaan kolmiota ADE.

Koska DE muodostaa halkaisijan, voimme käyttää viime viikon todistustamme osoittaaksemme 2x1 = 2y1.

Tarkastellaan nyt kolmiota EDB.

Samalla logiikalla _2x² = _y² .

Näiden yhtälöiden lisääminen:

_2x1 + _2x2 = _y1 + _y2

2( _x1 + _x2 ) = _y1 + _y2

2x = y

Ja olemme valmiita tapauksen 2 kanssa.

Katsotaanpa tapausta 3.

Tässä pyrimme osoittamaan, että 2x ₁ = y ₁ .

Tapauksesta 1:

_2x² = _y²

2(x ₁ + x ₂ ) = y < ₁ + y ₂

Vähentämällä ylempi yhtälö alemmasta yhtälöstä:

2x ₁ = y ₁

Ja olemme todistaneet tapauksen 3.

Logiikkapulman vastaus

Vain väittämä 9 pitää paikkansa.

Logiikkapulman ratkaisu

Meillä on kymmenen keskenään ristiriitaista väittämää. Jos kymmenen ihmistä sanoo eri asioita, joko vain yksi heistä on oikeassa tai kukaan heistä ei ole.

Tarkastellaan tapausta, jossa kaikki kymmenen väittämää ovat vääriä. Se tekisi väitteestä numero 10 tosi. Se tekisi vain yhdeksän väittämää vääriä. Kyseessä on siis ristiriita. Väittämän täytyy olla tosi. Mutta mikä?

Jos yksi väittämä on tosi, niin yhdeksän on väärin. Väite numero 9 sanoo näin. Näin ollen vain väittämä 9 on tosi.