Suuri Zoom-puhelun matematiikkapulma
Seuraava kysymys esitettiin uutiskirjeessäni viime viikolla. Jos tarvitset muistutusta, tässä on kysymys.
Kysymys
Oletetaan, että kaikki Yhdysvaltain edustajainhuoneen 435 äänioikeutettua jäsentä osallistuvat samaan Zoom-puheluun, jonka on määrä alkaa klo 9.00–10.00. Koko puheluun osallistuminen ei kuitenkaan ole pakollista, vaan ainoastaan osaan siitä. Jokainen jäsen valitsee satunnaisesti tarkan ajankohdan puheluun liittymiseen ja siitä poistumiseen jossain tuon tunnin sisällä.
Mikä on todennäköisyys sille, että ainakin yksi edustaja on päällekkäin jokaisen muun edustajan kanssa puhelussa? Toisin sanoen, että hän näkee jokaisen muun jäsenen kasvot hänen puhelunsa aikana, ei välttämättä kaikkien samaan aikaan.
Vieritä näitä kuvia ohi nähdäksesi vastaukseni ja ratkaisuni.

Vastaus
2/3
Ratkaisu
Yleinen strategiani kysymyksissä, joihin osallistuu suuri joukko ihmisiä, on aloittaa kahdella ihmisellä. Kun löydän vastauksen, siirryn kolmeen. Sitten, jos se ei ole liian vaikeaa, siirryn neljään. Jos näen säännön, on hyvät mahdollisuudet, että se pätee mille tahansa määrälle ihmisiä.
Perusmatematiikan kertaus
Ennen kuin jatkan, aion käyttää usein combin(x,y)-funktiota. Tämä on tapojen lukumäärä, joilla voidaan valita y esinettä x esineen joukosta. Esimerkiksi tapojen lukumäärä, joilla voidaan valita viisi korttia 52:sta, joissa järjestyksellä ei ole väliä, on combin(52,5) = 2 598 960. Vastaus voidaan ilmaista muodossa x! / (y! * (xy)!).
Tässä tapauksessa huutomerkki ei tarkoita, että huudan, vaan se edustaa kertomafunktiota. Tämä on kuinka monta tapaa järjestää mikä tahansa määrä kohteita. Esimerkiksi, jos sinun täytyy lukea kuusi kirjaa yksi kerrallaan, mahdollisten järjestysten lukumäärä on 6!. Yleisessä tapauksessa n on vastaus 1*2*3*…*n. Kuuden kirjan tapauksessa vastaus on 1*2*3*4*5*6 = 720.
Kahden hengen tapaus
Ratkaistaanpa ongelma kahden hengen tapauksessa. Tarkoilla kellonajoilla, jolloin ihmiset tulevat ja lähtevät puhelusta, ei ole väliä, ainoastaan tapahtumien järjestyksellä. Käytetään kirjainta edustamaan tiettyä henkilöä, joka tulee puheluun/lähtee siitä. Vasemmalta alkaen tietyn kirjaimen ensimmäinen käyttökerta edustaa puheluun liittymistä ja toinen sen poistumista.
Puheluhistorian neljästä kohdasta A-kirjaimen voi sijoittaa combin(4,2)=6 tavalla:
1. AABB
2. ABAB
3. ABBA
4. BAAB
5. BABA
6. BBAA
Tarkistetaan, olivatko molemmat soittajat paikalla samaan aikaan kussakin tilanteessa:
1. AABB - Ei, A tuli ja lähti ennen kuin B liittyi puheluun.
2. ABAB - Kyllä, B:n saapumisen ja A:n lähdön välillä oli päällekkäisyyttä.
3. ABBA - Kyllä, B:n saapumisen ja B:n lähdön välillä oli päällekkäisyyttä.
4. BAAB - Kyllä, A:n saapumisen ja A:n lähdön välillä oli päällekkäisyyttä.
5. BABA - Kyllä, A:n saapumisen ja B:n lähdön välillä oli päällekkäisyyttä.
6. BBAA - Ei, B tuli ja lähti ennen kuin A liittyi puheluun.
Jokainen skenaario on yhtä todennäköinen. Neljässä kuudesta oli päällekkäisyyksiä, joten päällekkäisyyden todennäköisyys kahden henkilön tapauksessa on 2/3.
Kolmen hengen tapaus
Kolmen henkilön tapauksessa puheluhistorioiden lukumäärä on tulo siitä, kuinka monella tapaa henkilö A voi valita kaksi paikkaa kuudesta historiassa, ja kuinka monella tapaa henkilö B voi valita kaksi jäljellä olevasta neljästä paikasta. Tämä on yhtä kuin combin(6,2)*combin(4,2) = 15*6 = 90.
Olisi työlästä luetella kaikki 90. Yksinkertaistetaan asioita olettamalla, että henkilö A liittyy ensin. Jonkun on oltava ensimmäinen, joten se voi yhtä hyvin olla A.
Tarkastellaan ensin tilannetta, jossa seuraava tapahtuma puheluhistoriassa on A:n poistuminen. Esitetään tämä muodossa AA????. Riippumatta siitä, miten B ja C tulevat ja poistuvat puhelusta, kukaan ei mene päällekkäin A:n kanssa. Näin ollen AA-skenaarion onnistumisen todennäköisyys on 0. Itse AA-skenaarion todennäköisyys on 1/5, koska sen jälkeen, kun A otti ensimmäisen paikan, seuraavaksi oli viisi mahdollista tapahtumaa – A, B, B, C ja C.
Tarkastellaan toiseksi tilannetta, jossa A liittyy ensin, B tulee seuraavaksi ja sitten A poistuu. Tässä tapauksessa B edustaa ketä tahansa muuta henkilöä kuin A (joka on jo lopettanut puhelun). Tätä esitetään muodossa ABA???. Loput sijoitettavat kirjaimet ovat B, C ja C. Kolmesta tavasta, joilla B voidaan sijoittaa (BCC, CBC ja CCB), CBC ja CCB johtavat siihen, että B on päällekkäin sekä A:n että C:n kanssa. Näin ollen onnistumisen todennäköisyys ABA-skenaariossa on 2/3. Itse skenaarion todennäköisyys on pr(kukaan muu kuin A liittyy)*pr(A poistuu) = (4/5)*(1/4) = 1/5, jossa pr(x) edustaa tapahtuman x todennäköisyyttä.
Kolmanneksi, tarkastellaan tilannetta, jossa A liittyy ensin, B tulee seuraavaksi ja sitten B poistuu. Tätä esitetään muodossa ABB???. Loput sijoitettavat kirjaimet ovat A, C ja C. Kolmesta tavasta, joilla A voidaan sijoittaa (ACC, CAC ja CCA), CAC ja CCA johtavat siihen, että A menee päällekkäin sekä B:n että C:n kanssa. Näin ollen onnistumisen todennäköisyys ABB-skenaariossa on 2/3. Itse skenaarion todennäköisyys on pr(kukaan muu kuin A liittyy)*pr(B poistuu) = (4/5)*(1/4) = 1/5.
Neljänneksi, tarkastellaan tilannetta, jossa A liittyy ensin, B tulee seuraavaksi ja sitten C liittyy. Tätä esitetään muodossa ABC??? Jäljelle jäävät kirjaimet ovat A, B ja C. On helppo nähdä, että aina kun A poistuu puhelusta, hän menee päällekkäin B:n ja C:n kanssa. Joten onnistumisen todennäköisyys tässä skenaariossa on 1. Itse skenaarion todennäköisyys on pr(kukaan muu kuin A liittyy)*pr(kolmas henkilö liittyy) = (4/5)*(2/4) = 2/5.
Käsittelimme kaikkia mahdollisia skenaarioita, kuten todennäköisyyksien (1/5 + 1/5 + 1/5 + 2/5) summasta 1 käy ilmi. Laskemalla kunkin skenaarion todennäköisyyden ja sen onnistumistodennäköisyyden pistetulon saamme: (1/5)*0 + (1/5)*(2/3) + (1/5)*(2/3) + (2/5)*1 = 0 + 2/15 + 2/15 + 6/15 = 10/15 = 2/3.
Neljän hengen tapaus
Jos minulla olisi kiire, voisin arvata vastauksen alkuperäiseen kysymykseen olevan 2/3, koska se pätee sekä kahden että kolmen hengen tapauksiin. Se kuitenkin vaikuttaa niin epätyydyttävältä, joten siirrytäänpä neljän hengen tapaukseen. Voin jakaa sen kymmeneen mahdolliseen skenaarioon seuraavasti:
- AA??????
Skenaarion todennäköisyys = 1/7
Onnistumisen todennäköisyys = 0 (kukaan ei voi olla päällekkäin A:n kanssa)
- ABA????
Skenaarion todennäköisyys = 1/7
Onnistumisen todennäköisyys = 16/30
- ABBA????
Skenaarion todennäköisyys = 1/35
Onnistumisen todennäköisyys = 0 (kukaan ei voi olla päällekkäin B:n kanssa)
- ABBC????
Skenaarion todennäköisyys = 4/35
Onnistumisen todennäköisyys = 2/3
- ABCA????
Skenaarion todennäköisyys = 4/35
Onnistumisen todennäköisyys = 5/6
- ABCBA????
Skenaarion todennäköisyys = 1/35
Onnistumisen todennäköisyys = 2/3
- ABCBC????
Skenaarion todennäköisyys = 1/35
Onnistumisen todennäköisyys = 2/3
- ABCBD????
Skenaarion todennäköisyys = 2/35
Onnistumisen todennäköisyys = 1 (A menee päällekkäin B:n, C:n ja D:n kanssa)
- ABCC????
Skenaarion todennäköisyys = 4/35
Onnistumisen todennäköisyys = 5/6
- ABCD????
Skenaarion todennäköisyys = 8/35
Onnistumisen todennäköisyys = 1 (A menee päällekkäin B:n, C:n ja D:n kanssa)
Pahoittelen, etten käynyt läpi laskelmia jokaisessa tilanteessa yhtä huolellisesti, mutta en halunnut tämän ratkaisun kestävän liian kauan ja halusin jättää lukijalle hieman työtä.
Seuraava taulukko yhteenvetää kaikki kymmenen neljän hengen tapauksen skenaariota.
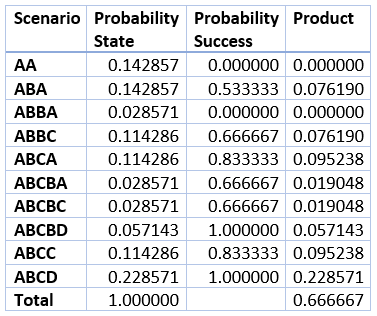
Taulukon oikeassa alakulmassa olevassa solussa on todennäköisyys 2/3.
Yhteenveto
Olemme osoittaneet todennäköisyydeksi 2/3 kahden, kolmen ja neljän hengen tapauksissa. On loogista, että tämä todennäköisyys todennäköisesti pätee edelleen mille tahansa määrälle ihmisiä. Simulaatiot ja minua fiksumpien ihmisten laskelmat ovat vahvistaneet tämän todeksi.


