Kuinka voittaa hinta on oikea 'silloin tai nyt' -pelissä

Yksi uhkapelien ulkopuolisista kiinnostuksen kohteistani on peliohjelmat. Erityisesti rakastan monien niistä peliteorian puolta. Erityisesti "The Price is Right" -ohjelmaa. Haluaisin kirjoittaa kirjan matemaattisesti optimaalisesta tavasta pelata kaikkia kyseisen ohjelman pelejä ilman hintoja koskevaa tietoa.

Tässä uutiskirjeessä käsittelen vain yhtä peliä "Nyt tai sitten".

Tässä ovat säännöt:

1. Pelissä on pyöreä pelilauta, jossa on kuusi viipaletta, kuin Trivia Pursuit -pelissä. Keskustelun helpottamiseksi numeroidaan viipaleet näin.
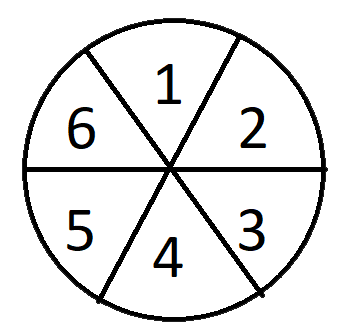
2. Jokainen hinta on joko tarkka hinta "Nyt" tai joskus noin kymmenen vuotta sitten.
3. Pelaaja voi valita minkä tahansa palan.
4. Pelaajan täytyy arvata, näyttääkö valitun osan esineen hinnan "Nyt"- vai "Silloin".
5. Pelaajan täytyy saada kolme peräkkäistä viipaletta oikein ruutuun (esimerkiksi viipaleet 4, 5 ja 6) voittaakseen pelin.
6. Ohjelmassa sitä ei mainita, mutta perinteisesti on ollut neljä ”Nyt”-kohtaa ja kaksi ”Sitten”-kohtaa.

Yllä olevat tiedot mielessä pitäen on olemassa tapa taata tämän pelin voitto tietämättä minkään hintaa. Säännöt 2 ja 6 ovat kriittisiä. Luulen, että harvat kilpailijat tuntevat molemmat säännöt.

Tässä on Youtube-esimerkki.

Huomaa kohdassa 3:52, kuinka Drew toteaa aivan oikein, että pelaajan täytyy saada pretzelit oikein voittaakseen; mutta sitten hän lisää: "Voit kuitenkin mennä minne haluat."

Linkki fanisivustolle: https://priceisright.fandom.com/wiki/Now....or_Then

Vastaus paljastuu esityksestä otetuista kuvista.

Tässä on vastaus:

Valitse ensin mitkä tahansa kolme viipaletta peräkkäin ja arvaa "Nyt" kaikille niille. Esimerkiksi kolmelle ylimmäiselle, jotka ovat 6, 1 ja 2.

Näin edetään sen mukaan, mitä tapahtui kolmelle ensimmäiselle viipaleelle.

1. Jos kaikki kolme olivat NYT, niin voitit!
2. Jos mitkä tahansa kaksi olivat SILLOIN, niin loput täytyy olla NYT. Varmista voitto valitsemalla NYT kolmelle muulle osiolle.
3. Jos saat yhden SIINÄ-sanan jompaankumpaan päähän (siivu 2 tai 6), arvaa mitä tahansa kahdelle SIIN-siivua lähimpänä olevalle siivulle. Jos löydät toisen SIIN-siivun, jäljellä olevan siivun täytyy olla NYT. Jos et löydä toista SIIN-siivua, viimeisen SIIN-siivun täytyy olla viimeinen siivu. Huomaa, että tämä oli tilanne yllä mainitsemassani esimerkkivideossa, mutta pelaaja ei noudattanut Drew'n vihjettä etsimällä tietoa muista kuin tarvittavista siivuista.
4. Jos saat toisen SIIS keskelle (lohko 1), valitse NYT lohkoille 3 ja 5. Jos molemmat ovat NYT, voitat valitsemalla SITTEN lohkolle 4. Jos toinen on SITTEN, valitse NYT lohkolle 4 voittaaksesi.

Toisin sanoen, kyse on siitä, että tiedetään, että on olemassa kaksi SIIS-viipaletta, ja niiden sijainnin rajaamisesta.

Ensi viikon uutiskirjeessä aion antaa teille kysymyksen nyt, jotta teillä olisi kokonainen viikko aikaa nauttia sen työstämisestä!

Oletetaan, että kaikki Yhdysvaltain edustajainhuoneen 435 äänioikeutettua jäsentä osallistuvat samaan Zoom-puheluun, joka on ajoitettu klo 9–10. Koko puheluun osallistuminen ei kuitenkaan ole pakollista, vaan ainoastaan osaan siitä. Jokainen jäsen valitsee satunnaisesti tarkan ajankohdan puheluun liittymiseen ja poistumiseen tuon tunnin sisällä.

Mikä on todennäköisyys, että ainakin yksi edustaja on päällekkäin jokaisen muun edustajan kanssa puhelussa? Toisin sanoen, hän näkee jokaisen muun jäsenen kasvot hänen puheluaikanaan, mutta ei välttämättä kaikkien samaan aikaan.

Kirjoittanut: Michael Shackleford