Pythagoraan kaavan todistus

Tällä viikolla todistan klassisen Pythagoraan kaavan, jonka mukaan suorakulmaisessa kolmiossa sivujen neliöiden summa on yhtä suuri kuin hypotenuusan neliö. Tunnetuin esimerkki on suorakulmainen kolmio, jonka sivut ovat 3, 4 ja 5. Huomaa 3 ² + 4 ² = 5 ^2. Ennen kuin pääsemme siihen, esittelen kuitenkin tavanomaisen viikoittaisen logiikkapulman.

Logiikkapulma

Hajamielinen antiikin filosofi unohti vetää seinällä roikkuvan ison kellonsa. Hänellä ei ollut radiota, televisiota, puhelinta, internetiä tai mitään muutakaan keinoa ajan mittaamiseen. Niinpä hän matkusti jalan ystävänsä luo muutaman mailin päähän suoraa aavikkotietä pitkin. Hän yöpyi ystävänsä luona ja palattuaan kotiin hän osasi asettaa kellonsa. Mistä hän tiesi?

Vastaus on uutiskirjeen lopussa.

Pythagoraan kaavan todistus

Tarkastellaan seuraavaa kaaviota, joka koostuu suuresta neliöstä, joka on jaettu neljään yhtä suureen suorakulmaiseen kolmioon, ja pienemmästä neliöstä keskellä. Keskellä on neliö, koska minkä tahansa kolmion kulmien summa on 180 astetta. Todistin tämän 13. marraskuuta 2025 uutiskirjeessäni .

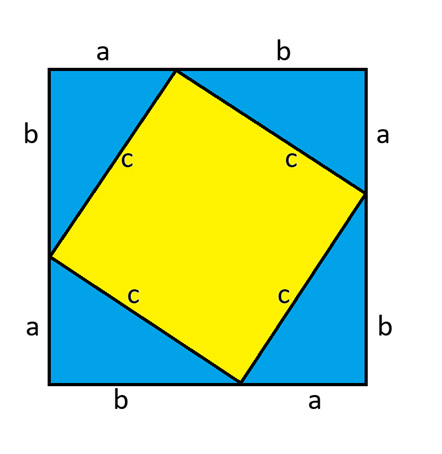
Suuren neliön pinta-ala on (a+b) ^² . Kunkin kolmion pinta-ala on ab² . Keskellä olevan keltaisen neliön pinta-ala on ^c² . Yhtälöimällä suuren neliön pinta-ala sisäosien summaan saadaan:

6; fonttiperhe: 'Open Sans', sans-serif; väri: #313131 !tärkeä;">(a+b) ² = 4 ab 2 + c ²

^a² + 2ab + ^b² = 2ab + ^c²

Vähentämällä 2ab molemmista puolista saadaan:

^a² + ^b² = ^c²

Logiikkapulman ratkaisu

1. Professori veitti kellon ja asetti sen mielivaltaiseen aikaan.
2. Saavuttuaan ystävänsä luo hän panee merkille saapumisajan.
3. Lähtiessään hän kirjaa muistiin lähtöaikansa ja laskee ystävän luona viettämänsä ajan vähentämällä saapumisaikansa lähtöajasta.
4. Hän on varovainen kävelemään takaisin samaa vauhtia kuin hän käveli ystävänsä luokse.
5. Kun hän palaa kotiin, hänen kellonsa on siirtänyt eteenpäin ystävän luona vietetyn ajan plus kävelyajan. Hän voi laskea kävelyajan vähentämällä ystävän luona vietetyn ajan kokonaisajasta. Sitten hän voi laskea yksisuuntaisen matkan ajan jakamalla kokonaiskävelyajan kahdella.
6. Sitten hän voi asettaa kellonsa ajan, jolloin hän lähti ystävän luota, plus yhdensuuntaisen kävelyn ajan.

Katsotaanpa esimerkkiä.

Väärä kello on kierretty ja asetettu kello 12.00:een. Todellisuudessa kello 8.00 hän saapuu ystävänsä luo. Kello 13.00 hän lähtee ja huomioi viiden tunnin vierailun. Palattuaan hän huomaa kellonsa olevan kello 8.00. Kun viiden tunnin vierailusta vähennetään, se tarkoittaa, että hän käveli yhteensä kolme tuntia. Se tarkoittaa 1,5 tuntia suuntaansa. Jos hän lähti kello 13.00 ja käveli 1,5 tuntia, kellon täytyy nyt olla 2.30, johon hän sitten asettaa kellonsa.