Todiste harmonisen sarjan hajaantumisesta

Tämän viikon todistus on, että harmoninen sarja suppenee. Ennen kuin pääsemme siihen, esittelen kuitenkin tavanomaisen viikoittaisen logiikkapulman.

Logiikkapulma

Maanantaina sairaalan lastenhuoneessa oli kaksi vauvaa, yksi poika ja yksi tyttö.

Tiistaina perheeseen lisätään uusi vauva.

Keskiviikkona valitaan vauva sattumanvaraisesti. Se on poika.

Mikä on todennäköisyys sille, että tiistaina syntynyt vauva oli poika?

Todiste harmonisen sarjan hajaantumisesta

Harmoninen sarja on kaikkien kokonaislukujen käänteislukujen joukko. Toisin sanoen, 1 1 , 1 2 , 1 3 , 1 4 ,6; font-family: 'Open Sans', sans-serif; color: #313131 !important;"> 1 5 ,…, 1 ∞ . Sarjaa sanotaan divergoivaksi, jos sen kaikkien jäsenten summa on ääretön. Tämä ei ole ilmeistä harmonisen sarjan tapauksessa, koska jäsenet pienenevät äärettömän pieniksi. Todistetaan kuitenkin, että summa on todellakin ääretön.

Menetelmä 1: Vertailutesti

Jos voin todistaa, että toinen sarja, jossa on yhtä paljon tai vähemmän jäseniä, on divergentti, niin täytyy todistaa myös harmonisen sarjan olevan divergentti.

Harmoninen sarja: 1 1 , 1 2 , 1 3 , 1 4 , 1 5 , 1 6 ,6; fonttiperhe: 'Open Sans', sans-serif; väri: #313131 !tärkeä;"> 1 7 , 1 8 , 1 9 , 1 10 , 1 11 , 1 12 , 1 13 ,…, 1 ∞ .

Sarja 2: 1 1 , 1 2 ,6; fonttiperhe: 'Open Sans', sans-serif; väri: #313131 !tärkeä;"> 1 4 , 1 4 , 1 8 , 1 8 , 1 8 , 1 16 , 1 16 , 1 16 , 1 16 ,6; fonttiperhe: 'Open Sans', sans-serif; väri: #313131 !tärkeä;"> 1 16 , 1 16 , 1 16 , 1 32 ,…, 1 ∞ .

Sarja 2 alkaa samoilla kahdella jäsenellä kuin harmoninen sarja. Sitten jokaisella n > = 2 se toistuu 1 2 ⁿ x 2 ^n-1 kertaa. Huomaa, että jokainen sarjan 2 jäsen on yhtä suuri tai pienempi kuin harmonisen sarjan jäsen. Sarja 2 voidaan jakaa ryhmiin, joiden summa on 1 2 ⁿ X 2 ^n-1 = 1 2 . Havainnollistan tätä antamalla jokaiselle ryhmälle eri värin:

Sarja 2: 1 1 ,6; fonttiperhe: 'Open Sans', sans-serif; väri: #313131 !tärkeä;"> 1 2 , 1 4 , 1 4 , 1 8 , 1 8 , 1 8 , 1 16 , 1 16 , 1 16 , 1 16 ,6; fonttiperhe: 'Open Sans', sans-serif; väri: #00A0D1 !tärkeä;"> 1 16 , 1 16 , 1 16 , 1 16 , 1 32 (16 kertaa), 1 64 (32 kertaa) …, 1 ∞

1 + ( 1 2 X ∞) = ∞

Menetelmä 2: Differentiaali- ja integraalilaskenta

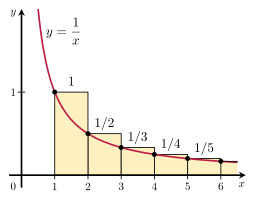
Huomaa, että keltaisten suorakulmioiden pinta-ala on suurempi kuin punaisen käyrän alla oleva pinta-ala. Punaisen käyrän pinta-ala on:

∫ ₁ ^∞ 1 x dx = ln(x) + c 1:stä ∞:een = ln(∞) + c – ln(1) – c = ∞.

Logiikkapulman ratkaisu

Lyhyt vastaus

Tapahtuneelle on kaksi mahdollista selitystä. Kutsutaan niitä X:ksi ja Y:ksi.

X = Poika lisättiin tiistaina ja poika havaitaan keskiviikkona. Tämän todennäköisyys on (1/2) * (2/3) = 2/6 = 1/3.

Y = Tyttö lisättiin tiistaina ja poika havaitaan keskiviikkona. Tämän todennäköisyys on (1/2)*(1/3) = 1/6.

X + Y = 1/3 + 1/6 = 1/2

Kysymys kuuluu, mikä on näiden kahden todennäköisyys. X on se, mitä tapahtui. Tämä olisi X/(X+Y) = (1/3)/(1/2) = 2/3.

Pitkä vastaus

Bayesilainen ehdollisen todennäköisyyden kaava sanoo, että Prob(A annettuna B) = Prob(A ja B)/Prob(B), missä prob(x) = minkä tahansa tapahtuman x todennäköisyys. Olkoon:

A = Poika lisätty tiistaina

6; font-family: 'Open Sans', sans-serif; color: #313131 !important; ">B = Poika havaittu keskiviikkona

Tässä tapauksessa:

Todennäköisyys(A annettu B) = Todennäköisyys(Poika lisätty tiistaina annettu poika havaittu keskiviikkona) = Todennäköisyys(Poika lisätty tiistaina ja poika havaittu keskiviikkona)/Todennäköisyys(Poika havaittu keskiviikkona).

Koska tiistain arvonnasta ei ole tietoa, on 50 %:n todennäköisyys sille, että tiistaina arvottiin poika. Olettaen, että tiistaina arvottu vauva oli poika, keskiviikkona arvotun vauvan todennäköisyys olisi 2/3.

Samoin, koska tiistain arvonnasta ei ole tietoa, on 50 %:n todennäköisyys sille, että tiistaina arvottiin tyttö. Olettaen, että tiistaina arvottu vauva oli tyttö, olisi 1/3:n todennäköisyys sille, että keskiviikkona arvottu vauva on poika.

Todennäköisyys sille, että poika arvottiin keskiviikkona, on yhtä kuin tod(poika lisättiin tiistaina)*tod(poika arvottiin keskiviikkona) + tod(tyttö lisättiin tiistaina)*tod(poika arvottiin keskiviikkona) = (1/2)*(2/3) + (1/2)*(1/3) = 1/2.

Todennäköisyys sille, että poika lisättiin tiistaina ja poika arvottiin keskiviikkona = (1/2) * (2/3) = 1/3.

Näin ollen vastaus on (1/3) / (1/2) = 2/3.