Kivi, paperi, sakset, miinus yksi

Pidämme edelleen taukoa Camino de Santiago -sarjassani ja käsittelemme peliä, joka tunnetaan nimellä "kivi, paperi, sakset miinus yksi".

Peli esitetään Squid Gamen toisen kauden ensimmäisessä jaksossa. Sarja itsessään on täynnä mielenkiintoista peliteoriaa, eikä tämä uusi peli ole poikkeus. Oletan, että lukija tuntee jo klassisen kivi-paperi-sakset-pelin säännöt.

Tässä ovat kivi-paperi-sakset miinus yksi -pelin säännöt.

1. 1. Pelin ensimmäisessä vaiheessa molemmat pelaajat pelaavat samanaikaisesti valitsemiaan symboleja, yhden kummallakin kädellä.
2. 2. Molemmille pelaajille annetaan hetki aikaa harkita seuraavaa siirtoaan.
3. 3. Pelin toisessa vaiheessa molemmat pelaajat vetävät samanaikaisesti toisen käden taaksepäin ja pelaavat siten toisen käden symbolin.
4. 4. Klassisen kivi, paperi, sakset -pelin säännöt ratkaisevat voittajan kummankin pelaajan jäljellä olevan yhden symbolin perusteella.

Seuraava video selittää säännöt.

Vaikka sääntöjen selitys oli oikea ja hauska, annetut neuvot olivat täysin VÄÄRÄT! Tämä mielipide perustuu oletukseen, että tasatilanteessa he pelaisivat uudelleen, ellei voittajaa olisi. Tässä on videolla näkyvä esimerkkitilanne:

Kolmio leikkii paperia ja saksia.

Ympyrä leikkii paperia ja kiveä.

Videolla kohdassa 1:18 rekrytoija sanoo, että Trianglen pitäisi pelata paperilla, koska riippumatta siitä, mitä Circle pelaa, peli päättyy ainakin tasapeliin.

Tarkastellaan tilannetta huolellisesti. Seuraava taulukko näyttää kaikkien neljän mahdollisen tilanteen lopputuloksen kolmiopelaajan näkökulmasta.

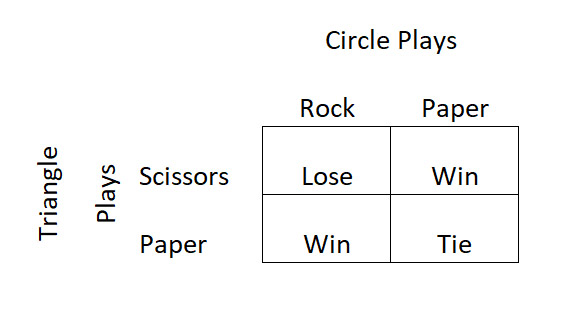
Kuten näet, Kolmion näkökulmasta on kaksi voittoa, yksi tapa tasata ja yksi tapa hävitä. Ympyrän näkökulmasta on päinvastoin, yksi tapa voittaa, yksi tasata ja kaksi tapa hävitä. Kolmio on siis etulyöntiasemassa.

Rekrytoija on oikeassa siinä, että jos Kolmio pelaa paperia, hän varmistaa ainakin tasapelin. Jos Ympyrä kuitenkin ennustaa tämän ajattelutavan, hän voisi päästä pois epäedullisesta asemastaan pelaamalla myös paperia, mikä johtaisi tasapeliin.

Jos Kolmio voisi ennustaa, että Ympyrä ajattelisi noin ja pelaisi Paperia, hän voisi voittaa pelin ottamalla riskin Saksilla. Jos Ympyrä kuitenkin näkisi sen, hän ottaisi riskin ja pelaisi kiveä murskaten Kolmion sakset. Toisaalta, jos Kolmio voisi ennustaa, että Ympyrä pelaisi Kiveä, hän tulisi takaisin ympyrään ja pelaisi Paperia, kukistaen Ympyrän kiven. Ja niin se jatkuu, ympäri ja ympäri, aivan kuten klassisessa Kivi-Paperi-Saksissa.

Oikea strategia molemmille osapuolille on satunnaistaminen! Katsotaanpa, miten se onnistuu.

Olkoon:

s = Todennäköisyyskolmio pelaa saksia

r = Todennäköisyysympyrä soittaa rockia.

Tällaisissa peliteorian kysymyksissä avainasemassa on löytää todennäköisyys, jossa odotettu voitto on sama riippumatta siitä, mitä vastustajasi pelaa. Näin ollen se ei auta vastustajaasi murtamaan strategiaasi.

Olkoon f(s) = Odotusarvoinen voitto, jos Kolmio pelaa saksipeliä.

= -rs + s(1-r) + (1-s)r + 0*(1-s)(1-r)

= -rs + s – rs + r – sr

= s + r – 3sr

Seuraavaksi otetaan derivaatta s:n suhteen ja asetetaan se nollaksi:

f'(s) = 1 – 3r = 0

r = 1/3.

Olkoon f(r) = Odotusarvoinen voitto, jos Circle pelaa rockia.

= rs - r(1-s) - (1-r)s + 0*(1-s)(1-r)

= rs–r + rs – s + rs

= -s - r + 3sr

Seuraavaksi otetaan derivaatta r:n suhteen ja asetetaan se nollaksi:

f'(r) = -1 + 3s = 0

s = 1/3.

Näin ollen optimaalinen strategia, toisin kuin rekrytoija sanoi, on:

1. • Kolmion tulisi leikkiä saksilla todennäköisyydellä 1/3 ja paperilla 2/3.
2. • Ympyrän tulisi soittaa rockia todennäköisyydellä 1/3 ja paperin 2/3.

Jos ainakin yksi pelaaja noudattaa tätä strategiaa, pelin lopputulos on seuraava:

1. • Kolmiovoitot = 4/9 = 44,44 %
2. • Tasapeli = 4/9 = 44,44 %
3. • Ympyrän voitot = 1/9 = 11,11 %

Laskemalla voiton +1:ksi, tasapelin 0:ksi ja tappion -1:ksi, Trianglen odotettu voitto on 1/3 = 33,3 %.

Kiitos lukemisesta ja toivottavasti nautit Squid Gamen toisesta kaudesta yhtä paljon kuin minä!