Round Robin -aikataulutus

Tämän viikon aiheena on round robin -turnauksen aikatauluttaminen. Ennen kuin jatkan, round robin on turnausmuoto, jossa jokainen pelaaja pelaa jokaista toista pelaajaa vastaan. Turnauksessa, jossa on n pelaajaa, otteluiden määrä on n(n-1)/2.

Olisi helppo listata kaikki n(n-1)/2 mahdollista paritusta n pelaajan kesken. Ihanteellista on kuitenkin tehdä se kierroksilla, joissa jokainen pelaaja pelaa kerran jokaisella kierroksella. Näin se tehdään parillisella määrällä pelaajia. Käytetään esimerkkinä kahdeksan pelaajan tilannetta. Seuraavassa kuvassa merkitsemme pelaajat A:sta H:hen ja näytämme kaksi pelaajaa ottelussa neljässä suorakulmiossa. Nämä neljä peliä muodostavat ensimmäisen kierroksen. Huomaa, miten kaikki pelaavat.

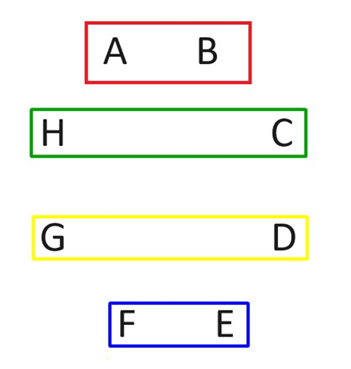
Toisella kierroksella pidä pelaaja A samassa paikassa. Sitten kaikki muut kiertävät myötäpäivään seuraavan kaavion mukaisesti.

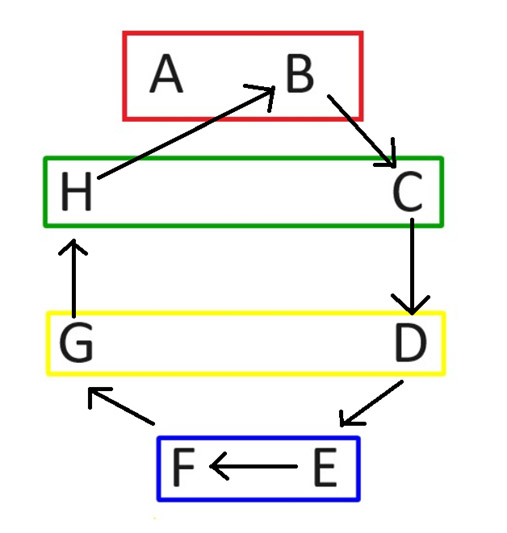
Kierroksen jälkeen toisen kierroksen ottelut näyttävät tältä:

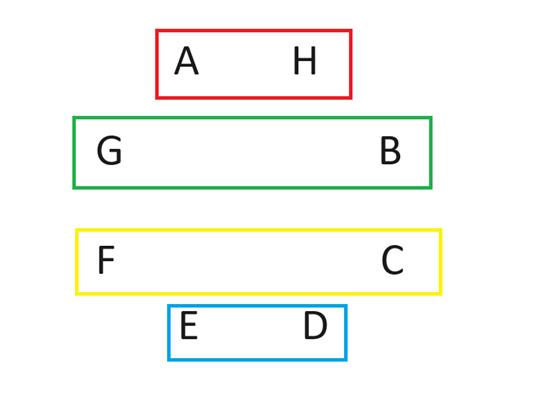
Jatka tätä, kunnes kaikki ovat pelanneet pelaajaa A vastaan. En osaa selittää, miksi tämä toimii, mutta se vain toimii. Se toimii parillisella määrällä pelaajia. Lisätietoja aiheesta saat hakemalla hakusanoilla ”ympyrämetodi” ja ”round robin”.

Seuraava taulukko näyttää kaikki kahdeksan pelaajan tapauksen kohtaamiset. Huomaa, kuinka kaikki pelaavat kaikkia vastaan tasan kerran.

Pyöristää	Pelaaja 1	Pelaaja 2
1	A	B
1	H	C
1	G	D
1	F	E
1	A	H
2	G	B
2	F	C
2	E	D
3	A	G
3	F	H
3	E	B
3	D	C
4	A	F
4	E	G
4	D	H
4	C	B
5	A	E
5	D	F
5	C	G
5	B	H
6	A	D
6	C	E
6	B	F
6	H	G
7	A	C
7	B	D
7	H	E
7	G	F

Parittomalla määrällä pelaajia turnaukseen lisätään vain yksi valepelaaja, jolloin saadaan parillinen määrä. Valepelaajaa vastaan pelaava saa vapaapäivän kyseisellä kierroksella, eli hän jättää pelaamatta. Joten kaikilla on yksi kierros, jonka aikana he pysyvät poissa pelistä. Näin se näyttäisi seitsemän pelaajan turnauksessa.

Pyöristää	Pelaaja 1	Pelaaja 2
1	A	B
1	hei hei	C
1	G	D
1	F	E
2	A	hei hei
2	G	B
2	F	C
2	E	D
3	A	G
3	F	hei hei
3	E	B
3	D	C
4	A	F
4	E	G
4	D	hei hei
4	C	B
5	A	E
5	D	F
5	C	G
5	B	hei hei
6	A	D
6	C	E
6	B	F
6	hei hei	G
7	A	C
7	B	D
7	hei hei	E
7	G	F

Oletetaan lopuksi, että kyseessä on tennisturnaus, jossa jokaisella kentällä on hyvä ja huono puoli. Huono puoli voisi luultavasti olla aurinkoon päin. Mikä on reilu tapa varmistaa, että jokaisella pelaajalla on hyvä ja huono puoli yhtä monta kertaa?

Ratkaistakseni ongelman käytän " Lisko Spock -laajennusta ", kuten Alkuräjähdysteoriassa selitetään. Tämä kivi-paperi-sakset-pelimenetelmä toimii millä tahansa parittolla määrällä symboleja. Jotta voidaan oikeudenmukaisesti määrittää, kumpi pelaaja saa hyvän puolen, tarkastellaan seitsemän pelaajan tapausta. Seuraava kaavio näyttää, kumpi pelaaja saa hyvän puolen, kuten nuoli osoittaa kohti pelaajaa, joka saa huonon puolen.

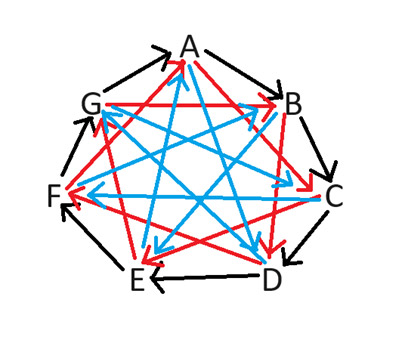
Esimerkiksi jos pelaajat B ja D pelaisivat, B saisi hyvän puolen, koska heidän välinen nuoli osoittaa D:tä kohti. Ei ole vaikea nähdä, miten piirsin kaavion. Nuolet osoittavat aina myötäpäivään. Ne on piirrettävä jokaiselle mahdolliselle määrälle aukkoja 1:stä 3:een.

Tällaista kaaviota ei kuitenkaan tarvitse piirtää, vaan riittää kirjainrengas. Tarkastellaan molempia tapoja kiertää ympyrää myötäpäivään päästäkseen pelaajalta toiselle. Vähemmän askeleita sisältävä reitti saa hyvän puolen. Tarkastellaan peliä pelaajien B ja F välillä. Myötäpäivään mennessä on neljä askelta pelaajasta B pelaajaan 4 ja kolme askelta pelaajasta F pelaajaan B. Koska kolme on vähemmän kuin neljä, pelaaja F saa hyvän puolen.

Seuraava taulukko näyttää kaikki mahdolliset vastakkainasettelut seitsemän pelaajan round robinissa, mukaan lukien ne pelaajat, jotka saavat hyvät ja huonot puolet.

Pyöristää	Hyvä puoli	Huono puoli
1	A	B
1	C	hei hei
1	D	G
1	E	F
2	A	hei hei
2	G	B
2	C	F
2	D	E
3	G	A
3	F	hei hei
3	B	E
3	C	D
4	F	A
4	E	G
4	D	hei hei
4	B	C
5	E	A
5	D	F
5	G	C
5	B	hei hei
6	A	D
6	C	E
6	F	B
6	G	hei hei
7	A	C
7	B	D
7	E	hei hei
7	F	G

Valitettavasti tämä puolien tasapainottamisstrategia ei toimi parillisella määrällä pelaajia. Tämä johtuu siitä, että ympyrän ympärillä olevat kaksi etäisyyttä ovat samat, kun kaksi pelaajaa ovat täysin vastakkaisilla puolilla. Pakottaessa tätä menetelmää voitaisiin käyttää kaikkiin muihin otteluihin, mutta pelaajien olisi valittava satunnaisesti, kun he ovat 180 asteen päässä toisistaan ympyrässä.

Näin pitkälle vien aihetta tällä kertaa. Pidätän oikeuden laajentaa sitä tulevassa uutiskirjeessä. Mahdollisia jatkokeskustelun aiheita ovat ottelut, joissa on kolme tai useampia pelaajia, sekä useiden kenttien käyttö, kun halutaan tasapainottaa sitä, kuinka usein kukin pelaaja pelaa kullakin kentällä.

Lopuksi toivotan teille kaikille hyvää Hanukkaa!

Kirjoittanut: Michael Shackleford