Kolmion kulmien summa on 180 astetta - lause

On yleisesti tiedossa, että minkä tahansa kolmion sisäkulmien summa on 180 astetta. Tässä uutiskirjeessä esitän yksinkertaisen todistuksen. Ennen sitä kuitenkin esittelen tavanomaisen viikoittaisen logiikkapulman.

Logiikkapulma

Kuninkaalla on 49 kultakolikkoa. Kolikot painavat 1, 2, 3, ... 49 grammaa kappale. Kuinka hän voi jakaa ne seitsemän pojan kesken siten, että jokainen poika saa seitsemän kolikkoa siten, että kolikkosumma on yhtä suuri?

Todiste siitä, että minkä tahansa kolmion sisäkulmien summa on 180 astetta.

Aloitan piirtämällä mielivaltaisen kolmion ja merkitsemällä kulmat.

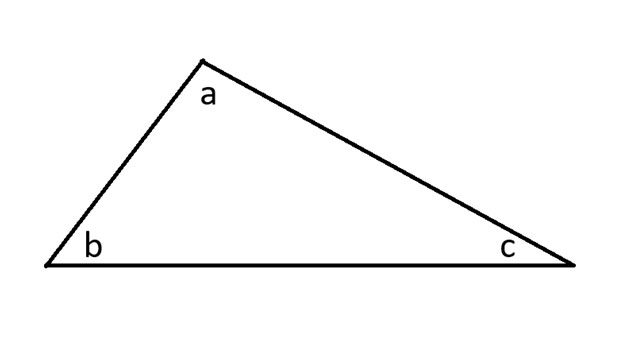
Seuraavaksi pidennän kolmion kaikkia kolmea sivua ja piirrän yhdensuuntaisen suoran, joka sivuaa kulmaa a.

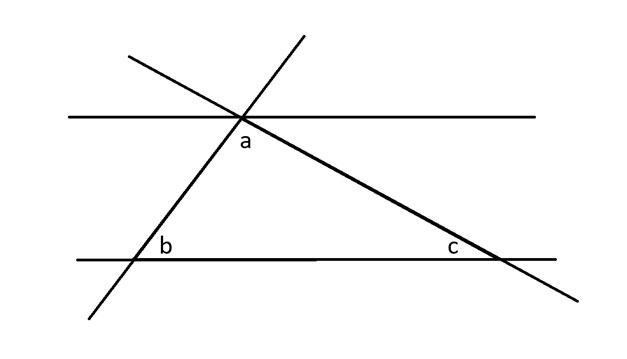
Seuraavaksi sovellan vastakkaisen kulman teoreemaa kulmaan b, joka sanoo, että kahden leikkaavan suoran vastakkaisissa kulmissa olevat kulmat ovat yhtä suuret.

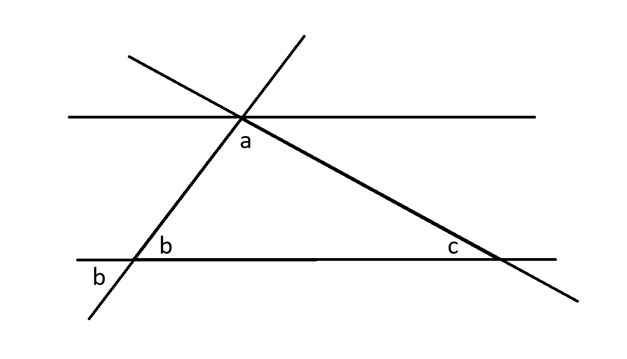
Kun lävistäjä leikkaa joukon yhdensuuntaisia suoria, se luo samat kulmat kohdassa, jossa se leikkaa jokaisen viivan. Käytän tätä näyttääkseni toisen b asteen kulman kulman a vieressä. Sitten teen saman asian kulman c kanssa.

6; fonttiperhe: 'Open Sans', sans-serif; väri: #313131 !tärkeä; ">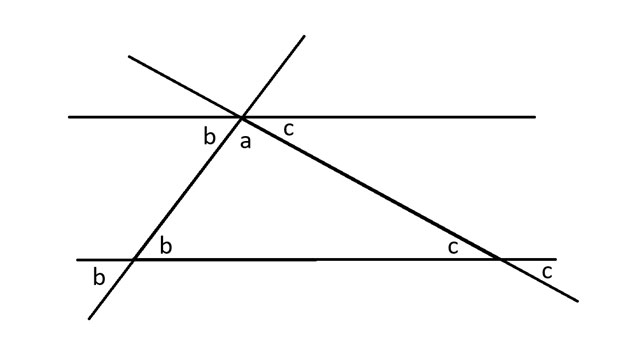

Ympyrässä on 360 astetta. Näin ollen puoliympyrässä on 180 astetta. Toisin sanoen, katsomalla ylimmän yhdensuuntaisen suoran alareunassa olevia kulmia, a + b + c = 180 astetta. Nämä ovat myös alkuperäisen kolmion kolme kulmaa. Näin ollen kolmion kulmien summa on 180 astetta.

Logiikkapulman ratkaisu

Tee taikaneliö ja anna jokaiselle pojalle yhden sarakkeen kolikot. Voit myös jakaa kolikot riveihin. "Miten teet 7x7-taikaneliön?", saatat kysyä. Seuraava tunnetaan siamilaisena menetelmänä, ja se keksittiin Intiassa kauan sitten.

Aloitetaan ruudukolla, joka on merkitty kuten 7x7 Taistelulaiva-lauta.

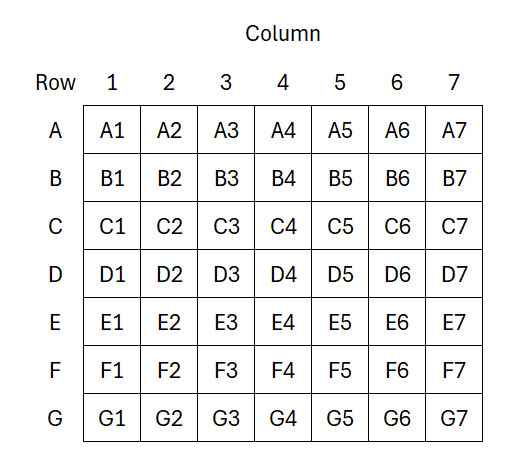
Aloita kirjoittamalla soluun A4 numero 1. Noudata sitten seuraavia sääntöjä:

1. Lisää aina 1 edelliseen lukuun seuraavaa sijoittelua varten.
2. Mene aina luoteeseen, ellei kyseinen ruutua ole jo varattu tai olet jo rivillä A tai sarakkeessa 7.
3. Jos olet rivillä A, siirry sarakkeeseen G seuraavan numeron saamiseksi.
4. Jos olet sarakkeessa 7, siirry sarakkeeseen 1 seuraavan numeron saamiseksi.
5. Puhelu A7 kiertää molemmat puolet ja päättyy G1:een.
6. Jos seuraava ruutu, johon sinun pitäisi mennä, on varattu, pudota alas seuraavaan ruutuun seuraavan numeron saamiseksi (sen pitäisi olla tyhjä).

Näin aloitamme:

1. 1 solussa A4.
2. Olemme rivillä A, joten siirrytään riville G ja lisätään soluun G5 luku 2.
3. Sitten laitamme F6:een luvun 3 ja E7:ään luvun 4.
4. Olemme sarakkeessa 7, joten kierrämme sarakkeen ja laitamme numeron 5 soluun D1.
5. Laita 6 soluun C2 ja 7 soluun B3.
6. Seuraavaksi tulisimme A4:ään, mutta siellä on numero 1. Joten pudotamme alas ja laitamme seuraavan numeron, 8, soluun C3.
7. Toista, kunnes Taikaneliö on täynnä.

Näin se näyttää valmistuttuaan:

jpg" />

Tämä menetelmä toimii mille tahansa parittoman kokoiselle taikaneliölle.

Päätä sitten, jaatko riveillä vai sarakkeilla. Jokainen poika saa yhden rivin/sarakkeen kolikot. Esimerkiksi jos jaat sarakkeiden mukaan, poika 1 saisi 30, 38, 46, 5, 13, 21 ja 22 kolikkoa.