Velho suosittelee
-
[VAL]11000 tervetuliaisbonus -
[VAL]3000 tervetuliaisbonus -
JOPA $777 BONUS
Ensimmäisten n kokonaisluvun summan todistus
Tällä viikolla teen yhden helpoimmista todistukseni, että 1+2+3+…+n = n(n+1)/2. Näytän sen kahdella hyvin intuitiivisella tavalla. Helpoin todistukseni tähän mennessä. Ennen kuin pääsemme siihen, esittelen kuitenkin tavanomaisen viikoittaisen logiikkapulmani.
Logiikkapulma
Alice, Bob ja Cole esittävät seuraavat lausunnot:
- • Alice: Bob on valehtelija.
- • Bob: Cole on valehtelija.
- • Cole: Alice ja Bob ovat valehtelijoita.
Kaikki kolme joko puhuvat aina totta tai valehtelevat aina. He kaikki tietävät kahden muun totuudenmukaisuuden. Kuka puhuu totta?
Katso vastaus ja ratkaisu uutiskirjeen lopusta.
Ensimmäisten n kokonaisluvun summan todistus
Kaikkien tulisi tietää, että n ensimmäisen kokonaisluvun summa on n(n+1)/2. Toisin sanoen, 1+2+3+…+n = n(n+1)/2. Esitän kaksi yksinkertaista todistusta siitä, miksi tämä on totta.
Menetelmä 1
On helppo nähdä, että jonon keskiarvo on (n+1)/2. Sarjan termien lukumäärä on n. Summa on yhtä suuri kuin termien lukumäärän tulo ja keskiarvotermi = n × (n+1)/2 = n(n+1)/2.
Samaa menetelmää voidaan käyttää summan löytämiseen millä tahansa alku- ja loppupisteellä. Kutsutaan alkulukua a:ksi ja loppulukua b:ksi. Keskiarvo on (a+b)/2. Termien lukumäärä on (a-b+1).Joten kaikkien sarjan lukujen summa on (a-b+1) × (a+b)/2.
Menetelmä 2
Seuraava menetelmä on helpompi selittää visuaalisesti. Tarkastellaan seuraavaa kaaviota, jossa siniset neliöt kuvaavat kokonaislukuja 1:stä 5:een.
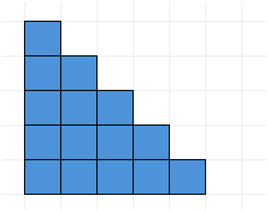
Seuraavaksi kopioi se ja aseta se alkuperäisen kappaleen viereen seuraavasti muodostaen suorakulmion.
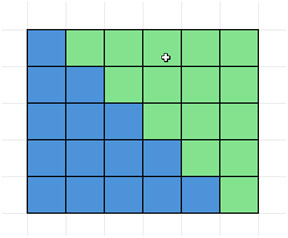
Huomaa, että yllä olevan suorakulmion mitat ovat 5 × 6. Yleisessä tapauksessa, kun kokonaisluvut 1:stä n:ään lasketaan yhteen, mitat ovat n × (n+1). Jaa sitten tämä pinta-ala kahdella, koska etsimme vain toisen kahdesta kappaleesta pinta-alaa. Näin ollen yhden kappaleen pinta-ala on n(n+1)/2.
Logiikkapulman ratkaisu
Kaikilla kolmella ihmisellä on kaksi mahdollista tilaa, totuudenmukainen tai valehteleva. Eli 2 3 = 8 mahdollisuutta. Luettelen ne kaikki alla olevassa taulukossa.
| Skenaario | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Alice | T | T | T | T | F | F | F | F |
| Bob | T | T | F | F | T | T | F | F |
| Cole | T | F | T | F | T | F | T | F |
Huomaa, että Bob ja Cole kutsuvat toisiaan valehtelijoiksi. Ainoa mahdollinen tapa on, jos toinen heistä on totuudenmukainen ja toinen valehtelija. Voimme siis sulkea pois neljä tilannetta, joissa Bobilla ja Colella on sama totuus. Jäljelle jäävät skenaariot 2, 3, 6 ja 7. Tarkastellaan niitä yksi kerrallaan.
Skenaariossa 2 oletetaan, että Alice on totuudenmukainen. Hänen totuudenmukainen lausuntonsa tekee Bobista valehtelijan. Bob on kuitenkin myös tässä skenaariossa totuudenmukainen, mikä johtaa ristiriitaan. Näin ollen skenaario 2 on poissuljettu.
Skenaariossa 3 oletetaan, että Alice on totuudenmukainen. Hän sanoo Bobin olevan valehtelija, mikä pitää paikkansa skenaarion 3 oletusten mukaisesti. Cole kuitenkin listataan totuudenmukaiseksi, ja hän sanoo Alicen valehtelevan. Alice ei voi olla totuudenmukainen ja valehtelija samaan aikaan, joten skenaario 3 hylätään.
Skenaariossa 7 oletetaan, että Alice valehtelee. Hän sanoo Bobin olevan valehtelija, mikä on totta. Se tekisi Alicesta kuitenkin totuudenmukaisen. Alice ei voi olla totuudenmukainen ja valehtelija samaan aikaan, joten skenaario 7 hylätään.
Jäljelle jää enää skenaario 6. Varmistetaan, että se toimii. Jos Alice olisi valehtelija, se tekisi Bobista totuudenmukaisen. Jos Bob olisi totuudenmukainen, niin Alice tai Bob tai molemmat olisivat totuudenmukaisia. Bob on totuudenmukainen, joten se tekee Colen väitteen vääräksi. Joten se pitää paikkansa. Bob on ainoa totuudenmukainen henkilö.