Video täydellisen sulkutilan todennäköisyydestä

Hei, täällä Mike, ja tämä video yrittää vastata kysymykseen: Mikä on täydellisen March Madness -kaavion täyttymisen todennäköisyys?

Oletan, että sinulla on jo jonkin verran perustietoa siitä, miten se toimii , mutta lyhyesti sanottuna, yhdessä pudotuspeliturnauksessa kilpailee 64 koripallojoukkuetta; se tarkoittaa, että otteluita on yhteensä 63.

He jakavat sen neljään divisioonaan , ja jokaisessa divisioonassa ensimmäisellä kierroksella 1. sijoitettu joukkue pelaa 16. sijoitettua joukkuetta vastaan, toiseksi sijoitettu pelaa 15. sijoitettua joukkuetta vastaan, kolmanneksi sijoitettu pelaa 14. sijoitettua joukkuetta vastaan ja niin edelleen. Sitten he valitsevat voittajat kaikista ensimmäisen kierroksen peleistä ja pelaavat sitten toisiaan vastaan toisella kierroksella, ja lopulta voittaja on vain yksi.

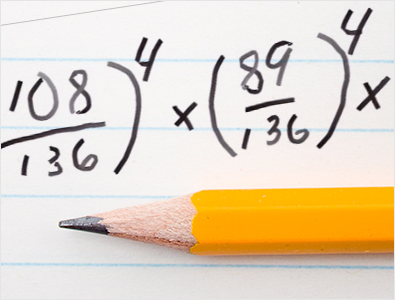
Nyt joka maaliskuu...

...mediassa nousee aina esiin kysymys täydellisen kaavion täyttymisen todennäköisyydestä, ja se saa niskakarvani pystyyn, kun kuulen luvun 1/9 kvintiljoona, 223 kvadriljoona, 372 biljoona, 36 miljardia, 854 miljoonaa, 781 000; uskoakseni. Tämä on yksinkertaisesti todennäköisyys ennustaa oikein 63 kolikonheittoa peräkkäin. En usko, että kukaan täyttää March Madness -kaaviota tällä tavalla, koska jotkut joukkueet ovat ilmiselvästi parempia kuin toiset. Esimerkiksi 1. sijoitettu on ilmiselvästi parempi kuin 16. sijoitettu.

Ennen kuin jatkan pidemmälle...

...sanotaanpa, että tämä video kuvattiin huhtikuussa 2018, joten se perustuu jokaiseen March Madness -peliin, jota on pelattu vuosina 1985–2018. Okei, halusin myös käsitellä toista YouTube-videota, jonka on tehnyt professori Jeff Bergen . Hän sanoo, että jollain strategialla, johon hän ei puutu, täydellisen pelikaavion todennäköisyys on 1/128 miljardia. Tämä luku on itse asiassa aika lähellä saamaani lukua.

Haastaisin professori Bergenin selittämään tarkemmin, miten hän saa tuon luvun, mutta aion selittää teille tarkemmin, miten minä saan oman luvuni. Strategiani on hyvin yksinkertainen. Valitsette aina jokaisessa pelissä korkeammalle sijoitetun joukkueen , ja lopulta jäljelle jää vain neljä ykköseksi sijoitettua joukkuetta, jolloin voitte valita satunnaisesti.

Ennen kuin joku kirjoittaa kommentteihin

Haluan sanoa, että tätä voi parantaa entisestään tarkastelemalla pelien nykyisiä kertoimia. Esimerkiksi kun kyseessä on 1. sijoitettu vastaan 1. sijoitettu, voi tarkastella Las Vegasin ulkomaille siirtymisen kertoimia nähdäkseen, miten voittomahdollisuuksilla on paremmat mahdollisuudet, mutta en aio mennä siihen tässä sen enempää.

Tässä videossa valitaan joka kerta paremmin sijoitettu joukkue, ja jälleen kerran, kun neljä ykkössijoitettua joukkuetta putoaa, valitaan satunnaisesti. Okei, siinä kaikki, mitä minun tarvitsee sanoa johdannoksi.

Haluan jo etukäteen pyytää anteeksi, että käytän videon seuraavassa osassa tablettia. Minulla on jo ollut paljon teknisiä ongelmia saada tämä toimimaan kunnolla, joten ajattelin kuvata johdannon tällä tavalla. Ilman pitkiä puheita, tässä on ohjeet täydellisen March Madness -kaavion todennäköisyyden laskemiseen juuri mainitsemallani strategialla.

Okei, tässä mennään:

Tämä on ensimmäinen videoni, jonka olen koskaan tehnyt luovalla kynätabletilla, jos sitä nyt niin voi kutsua. Olen aina halunnut tehdä tällaisia Khan Academy -tyyppisiä videoita, mutta uhkapeleistä ja matematiikasta. Nyt kun johdanto on ohi, mennään suoraan laskelmiin.

Todennäköisyys sille, että 1. sijoitettu voittaa 16. sijoitetun, on arvioitu olevan 135/136, koska tähän mennessä tällaisia otteluita on pelattu 136 ja 1. sijoitettu on voittanut 135 kertaa. Se on 1. sijoitetun voittotodennäköisyys missä tahansa ottelussa, joka on 99,26 %.

Kuitenkin...

...on neljä eri jakoa, joten sinun on saavutettava tämä neljällä eri kerralla, joten vie tämä neljänteen potenssiin.

On myös neljä eri peliä , joissa kakkossijoitettu pelaa 15. sijoitettua vastaan. Näin on käynyt 136 kertaa. Kakkossijoitettu on voittanut 127 kertaa. Historiallisten tietojen perusteella kakkossijoitetun joukkueen todennäköisyys voittaa 15. sijoitettu on 93,38 %, ja tämä on tehtävä neljä kertaa myös neljässä eri divisioonassa.

Samoin todennäköisyys sille, että 3. sijoitettu joukkue voittaa 14. sijoitetun, on 115 jaettuna 136:lla, ja tämäkin on tehtävä neljä kertaa. Sitten todennäköisyys sille, että 4. sijoitettu joukkue voittaa 13. sijoitetun, on 108 jaettuna 136:lla, ja jälleen kerran se korotetaan neljänteen potenssiin kaikkia niitä neljää peliä varten, jotka sinun on voitettava.

Todennäköisyys sille, että 5. sijoitettu joukkue voittaa 12. sijoitetun, on 89/136, mikä on noin 65,44 % ja neljänteen potenssiin korotettuna. Todennäköisyys sille, että 6. sijoitettu joukkue voittaa 11. sijoitetun, on 85/136, mikä on missä tahansa pelissä 62,5 %. Todennäköisyys sille, että 7. sijoitettu joukkue voittaa 10. sijoitettu, on 83/136. Kunkin pelin voittotodennäköisyys on 61,03 %. Todennäköisyys sille, että 8. sijoitettu joukkue voittaa 9. sijoitettu, on 71/136, ja jälleen kerran tämä on tehtävä neljä eri kertaa.

Jos voitat kaikki nämä pelit...

...pääset ensimmäisestä kierroksesta eteenpäin. Sitten toisella kierroksella 1. sijoitettu pelaa 8. sijoitettua vastaan. Tämä on tapahtunut tähän mennessä 72 kertaa, ja näistä 72 kerrasta 1. sijoitettu on voittanut 8. sijoitetun 58 kertaa. 1. sijoitetun todennäköisyys voittaa 8. sijoitettu on 80,56 %, ja sinun on silti tehtävä se neljä eri kertaa.

Sitten neljäs sijoitettu pelaa viidennellä sijoitetulla vastaan. Tämä on tapahtunut tähän mennessä 73 kertaa, ja neljäs sijoitettu on voittanut 41 kertaa, joten todennäköisyys jokaisessa pelissä on 56,16 %. Jaksoja on edelleen neljä, joten korotetaan neljänteen potenssiin.

Sitten kolme sijoitettua pelaavat kuutta sijoitettua vastaan. Kolme sijoitettua on voittanut 41 kertaa 70:stä, joten voittotodennäköisyys on 58,57 % jokaisesta pelistä. Lopuksi, päästäkseen toiselle kierrokselle, kaksi sijoitettua pelaavat seitsemää sijoitettua vastaan. Kaksi sijoitettu on voittanut 56 kertaa, ja näin on tapahtunut 79 kertaa, joten todennäköisyys joka kerta on 70,89 %. Okei, olettaen, että voitat kaikki nuo pelit, siirrytään kolmannelle kierrokselle, jossa 1 sijoitettu pelaa neljättä sijoitettua vastaan.

Tämä on tapahtunut turnauksen historiassa tähän mennessä 61 kertaa ja 1. sijoitettu on voittanut 44 kertaa, joten todennäköisyys on joka kerta 72,13 %. Tämän jälkeen 2. sijoitettu pelaa 3. sijoitettua vastaan. Näin on tapahtunut tähän mennessä 52 kertaa, ja näistä kerroista 32 kertaa 2. sijoitettu on voittanut. Jälleen kerran, tämän täytyy tapahtua neljä eri kertaa.

Olettaen, että voitat kaikki nuo pelit:

Sitten jäljelle jäävät vain 1. ja 2. sijoitetut joukkueet. Todennäköisyys sille, että 1. sijoitettu joukkue voittaa 2. sijoitetun, on 35/64, jälleen historiallisten otteluiden perusteella, ja tämän täytyy tapahtua neljä kertaa kaikissa neljässä divisioonassa.

Jos nyt pääset näin pitkälle... silloin olet voittanut kaikki neljä divisioonaa ja sinulla on joka kerta ykkösjoukkue ykkösenä. Tässä kohtaa aloitat satunnaisen valinnan. Tarvitset vielä kolme peliä selvittääksesi parhaan neljästä joukkueesta, ja kuten johdannossa sanoin, valitset vain satunnaisesti, joten voittomahdollisuutesi joka kerta ovat 1/2, ja vielä kolme peliä.

Se on voittotodennäköisyytesi käyttämällä strategiaani , ja tämä tarkoittaa todennäköisyyttä 1/42 743 890 552. Siinä se. Uskon, että tämä on tarkin luku täydellisen March Madness -kaavion täyttämiseksi.

Kuten johdannossa sanoin, voit parantaa tätä tarkastelemalla vedonlyöntimarkkinoiden nykyisiä kertoimia, ja kiitos tämän videon katsomisesta. Tiedän, ettei se ollut kovin hyvä.

Pitäkää tätä minulle oppimiskokemuksena, ja jälleen kerran, kaikki tämä on kirjallisena verkkosivustollani wizardofodds.com urheiluvedonlyöntiosiossa, ja etsikää sitten sivu, jossa opetetaan täydellisen March Madness -kaavion täyttäminen. En usko, että tässä on mitään muuta sanottavaa.

Joten kiitos katsomisesta.

Kirjoittanut: Michael Shackleford